多普勒原理在超声波流量测量领域的应用
时间:12-09
来源:互联网
点击:
多普勒效应是澳大利亚物理学家、数学家多普勒1842年首先从运动着的发声源中发现的现象:


Christian J. Doppler
让我们来首先了解一下多普勒效应。在日常生活中,我们都会有这种经验:当一列鸣着汽笛的火车向某观察者驶来时,他会发现火车汽笛的声调由低变高;当火车远离时,声调则由高变低。为什么会发生这种现象呢?这是因为声调的高低是由声波振动频率的不同决定的,如果频率高,声调听起来就高;反之声调听起来就低。这种现象称为多普勒效应。
多普勒效应是指物体辐射的波长因为光源和观测者的相对运动而产生变化,在运动的波源前面,波被压缩,波长变得较短,频率变得较高 ,在运动的波源后面,产生相反的效应,波长变得较长,频率变得较低 ,波源的速度越高,所产生的效应越大,根据光波红/蓝移的程度,可以计算出波源循着观测方向运动的速度,恒星光谱线的位移显示恒星循着观测方向运动的速度,这种现象称为多普勒效应。
多普勒效应不仅仅适用于声波,它也适用于所有类型的波,包括光波、电磁波。科学家Edwin Hubble使用多普勒效应得出宇宙正在膨胀的结论.他发现远处银河系的光线频率在变高,即移向光谱的红端.这就是红色多普勒频移,或称红移.若银河系正移向他,光线就成为蓝移.。



一、声波的多普勒效应
在日常生活中,我们都会有这种经验:当一列鸣着汽笛的火车经过某观察者时,他会发现火车汽笛的声调由高变低. 为什么会发生这种现象呢?这是因为声调的高低是由声波振动频率的不同决定的,如果频率高,声调听起来就高;反之声调听起来就低.这种现象称为多普勒效应,它是用发现者克里斯蒂安·多普勒(Christian Doppler,1803-1853)的名字命名的,多普勒是奥地利物理学家和数学家.他于1842年首先发现了这种效应.为了理解这一现象,就需要考察火车以恒定速度驶近时,汽笛发出的声波在传播时的规律.其结果是声波的波长缩短,好象波被压缩了.因此,在一定时间间隔内传播的波数就增加了,这就是观察者为什么会感受到声调变高的原因;相反,当火车驶向远方时,声波的波长变大,好象波被拉伸了. 因此,声音听起来就显得低沉.定量分析得到f1=(u+v0)/(u-vs)f ,其中vs为波源相对于介质的速度,v0为观察者相对于介质的速度,f表示波源的固有频率,u表示波在静止介质中的传播速度. 当观察者朝波源运动时,v0取正号;当观察者背离波源(即顺着波源)运动时,v0取负号. 当波源朝观察者运动时vs前面取负号;前波源背离观察者运动时vs取正号. 从上式易知,当观察者与声源相互靠近时,f1>f;当观察者与声源相互远离时,f1<f 。
二、多普勒效应在超声波流量测量领域的应用
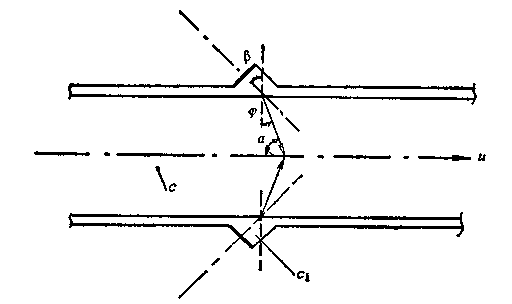
假设,超声波波束与流体运动速度的夹角为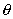 ,超声波传播速度为c,流体中悬浮粒子运动速度与流体流速相同,均为u.现以超声波束在一颗固体粒子上的反射为例,导出声波多普勒频差与流速的关系式. 如图所示,当超声波束在管轴线上遇到一粒固体颗粒,该粒子以速度u沿营轴线运动.对超声波发射器而言,该粒子以u cos a的速度离去,所以粒子收到的超声波频率f2应低于发射的超声波频率f1,降低的数值为
,超声波传播速度为c,流体中悬浮粒子运动速度与流体流速相同,均为u.现以超声波束在一颗固体粒子上的反射为例,导出声波多普勒频差与流速的关系式. 如图所示,当超声波束在管轴线上遇到一粒固体颗粒,该粒子以速度u沿营轴线运动.对超声波发射器而言,该粒子以u cos a的速度离去,所以粒子收到的超声波频率f2应低于发射的超声波频率f1,降低的数值为
f2-f1=-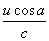 f1
f1
即粒子收到的超声波频率为
f2=f1-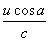 f1
f1
式中 f1――发射超声波的频率;
a――超声波束与管轴线夹角;
c――流体中声速。
固体粒子又将超声波束散射给接收器,由于它以u cos a 的速度离开接收器,所以接收器收到的超声波频率f3又一次降低,类似于f2的计算,f3可表示为
f3=f2-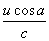 f2
f2
将f2的表达式代入上式,可得:
f3=f1(1-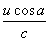 )2 =f1(1-2
)2 =f1(1-2 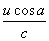 +
+ 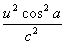 )
)
由于声速c远大于流体速度u,故上式中平方项可以略去,由此可得:
f3=f1(1-2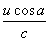 )
)
接收器收到的超声波频率与发射超声波频率之差,即多普勒频移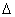 f1,可由下式计算:
f1,可由下式计算:
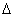 f=f1-f3=f1-f1(1-2
f=f1-f3=f1-f1(1-2 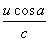 )=f1
)=f1 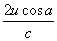 u=
u= 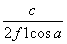
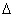 f
f
体积流量qv可以写成:
qv=uA=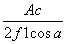
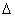 f
f
式中,A为被测管道流通截面积.
出以上流量方程可知,当流量计、管道条件及被测介质确定以后,多普勒频移与体积流量成正比,测量频移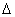 f就可以得到流体流量qv。
f就可以得到流体流量qv。
三、光波(包括电磁波)的多普勒效应
具有波动性的光也会出现这种效应,它又被称为多普勒-斐索效应. 因为法国物理学家斐索(1819-1896)于1848年独立地对来自恒星的波长偏移做了解释,指出了利用这种效应测量恒星相对速度的办法.光波与声波的不同之处在于,光波频率的变化使人感觉到是颜色的变化. 如果恒星远离我们而去,则光的谱线就向红光方向移动,称为红移;如果恒星朝向我们运动,光的谱线就向紫光方向移动,称为蓝移.


Christian J. Doppler
让我们来首先了解一下多普勒效应。在日常生活中,我们都会有这种经验:当一列鸣着汽笛的火车向某观察者驶来时,他会发现火车汽笛的声调由低变高;当火车远离时,声调则由高变低。为什么会发生这种现象呢?这是因为声调的高低是由声波振动频率的不同决定的,如果频率高,声调听起来就高;反之声调听起来就低。这种现象称为多普勒效应。
多普勒效应是指物体辐射的波长因为光源和观测者的相对运动而产生变化,在运动的波源前面,波被压缩,波长变得较短,频率变得较高 ,在运动的波源后面,产生相反的效应,波长变得较长,频率变得较低 ,波源的速度越高,所产生的效应越大,根据光波红/蓝移的程度,可以计算出波源循着观测方向运动的速度,恒星光谱线的位移显示恒星循着观测方向运动的速度,这种现象称为多普勒效应。
多普勒效应不仅仅适用于声波,它也适用于所有类型的波,包括光波、电磁波。科学家Edwin Hubble使用多普勒效应得出宇宙正在膨胀的结论.他发现远处银河系的光线频率在变高,即移向光谱的红端.这就是红色多普勒频移,或称红移.若银河系正移向他,光线就成为蓝移.。



一、声波的多普勒效应
在日常生活中,我们都会有这种经验:当一列鸣着汽笛的火车经过某观察者时,他会发现火车汽笛的声调由高变低. 为什么会发生这种现象呢?这是因为声调的高低是由声波振动频率的不同决定的,如果频率高,声调听起来就高;反之声调听起来就低.这种现象称为多普勒效应,它是用发现者克里斯蒂安·多普勒(Christian Doppler,1803-1853)的名字命名的,多普勒是奥地利物理学家和数学家.他于1842年首先发现了这种效应.为了理解这一现象,就需要考察火车以恒定速度驶近时,汽笛发出的声波在传播时的规律.其结果是声波的波长缩短,好象波被压缩了.因此,在一定时间间隔内传播的波数就增加了,这就是观察者为什么会感受到声调变高的原因;相反,当火车驶向远方时,声波的波长变大,好象波被拉伸了. 因此,声音听起来就显得低沉.定量分析得到f1=(u+v0)/(u-vs)f ,其中vs为波源相对于介质的速度,v0为观察者相对于介质的速度,f表示波源的固有频率,u表示波在静止介质中的传播速度. 当观察者朝波源运动时,v0取正号;当观察者背离波源(即顺着波源)运动时,v0取负号. 当波源朝观察者运动时vs前面取负号;前波源背离观察者运动时vs取正号. 从上式易知,当观察者与声源相互靠近时,f1>f;当观察者与声源相互远离时,f1<f 。
二、多普勒效应在超声波流量测量领域的应用

假设,超声波波束与流体运动速度的夹角为
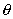 ,超声波传播速度为c,流体中悬浮粒子运动速度与流体流速相同,均为u.现以超声波束在一颗固体粒子上的反射为例,导出声波多普勒频差与流速的关系式. 如图所示,当超声波束在管轴线上遇到一粒固体颗粒,该粒子以速度u沿营轴线运动.对超声波发射器而言,该粒子以u cos a的速度离去,所以粒子收到的超声波频率f2应低于发射的超声波频率f1,降低的数值为
,超声波传播速度为c,流体中悬浮粒子运动速度与流体流速相同,均为u.现以超声波束在一颗固体粒子上的反射为例,导出声波多普勒频差与流速的关系式. 如图所示,当超声波束在管轴线上遇到一粒固体颗粒,该粒子以速度u沿营轴线运动.对超声波发射器而言,该粒子以u cos a的速度离去,所以粒子收到的超声波频率f2应低于发射的超声波频率f1,降低的数值为 f2-f1=-
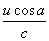 f1
f1即粒子收到的超声波频率为
f2=f1-
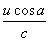 f1
f1式中 f1――发射超声波的频率;
a――超声波束与管轴线夹角;
c――流体中声速。
固体粒子又将超声波束散射给接收器,由于它以u cos a 的速度离开接收器,所以接收器收到的超声波频率f3又一次降低,类似于f2的计算,f3可表示为
f3=f2-
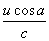 f2
f2将f2的表达式代入上式,可得:
f3=f1(1-
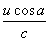 )2 =f1(1-2
)2 =f1(1-2 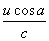 +
+ 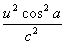 )
)由于声速c远大于流体速度u,故上式中平方项可以略去,由此可得:
f3=f1(1-2
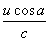 )
)接收器收到的超声波频率与发射超声波频率之差,即多普勒频移
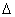 f1,可由下式计算:
f1,可由下式计算: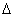 f=f1-f3=f1-f1(1-2
f=f1-f3=f1-f1(1-2 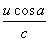 )=f1
)=f1 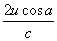 u=
u= 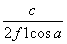
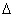 f
f体积流量qv可以写成:
qv=uA=
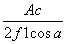
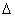 f
f式中,A为被测管道流通截面积.
出以上流量方程可知,当流量计、管道条件及被测介质确定以后,多普勒频移与体积流量成正比,测量频移
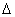 f就可以得到流体流量qv。
f就可以得到流体流量qv。三、光波(包括电磁波)的多普勒效应
具有波动性的光也会出现这种效应,它又被称为多普勒-斐索效应. 因为法国物理学家斐索(1819-1896)于1848年独立地对来自恒星的波长偏移做了解释,指出了利用这种效应测量恒星相对速度的办法.光波与声波的不同之处在于,光波频率的变化使人感觉到是颜色的变化. 如果恒星远离我们而去,则光的谱线就向红光方向移动,称为红移;如果恒星朝向我们运动,光的谱线就向紫光方向移动,称为蓝移.
- 基于nRF2401智能小区无线抄表系统集中器设计(04-30)
- 基于nRF2401智能无线火灾监控系统设计(04-01)
- 家居安防无线监控报警系统(04-02)
- 什么是原子钟(07-04)
- 基于nRF905智能小区照明控制系统设计(08-20)
- 航天飞机将退出历史舞台,专家讲解原因(11-09)
