基于多特征SVMs分类器的手语识别的研究
时间:12-07
来源:互联网
点击:
Hu不变矩特征量
利用矩不变量进行形体识别是模式识别中的一种重要的方法, Hu在1961年首先提出了矩不变量的概念。Hu首先提出代数不变矩的概念,并给出了一组基于通用矩组合的代数矩不变量。这些矩具有平移、尺度和旋转不变性,被称为Hu’s矩。
对于连续灰度函数 f(x, y),它的(p + q)阶二维原点矩Mpq 的定义为:
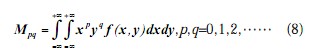
假设 f(x, y)为分段连续的有界函数,并且在x,y平面上有限区域内有非零值。根据唯一性定理,它的各阶矩存在且唯一地被 f(x, y)确定,反过来,f(x, y)也唯一地被它的各阶矩确定。
此外,还可以定义 f(x, y)的(p + q)阶中心矩μpq 为:
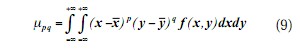
Hu首先提出了不变矩,他给出了连续函数矩的定义和关于矩的基本性质,证明了有关矩的平移不变性、旋转不变性以及比例不变性等性质,具体给出了具有平移不变性、旋转不变性和比例不变性的七个不变矩的表达式。
七个不变矩由二阶和三阶中心矩的线性组合构成,具体表达式如下:

实验中,使用了全部的7Hu不变矩特征量作为手语图像整体形状描述的特征向量。形成特征空间(M1, M2, M3, M4, M5, M6, M7),如表1所示。
表1手语字母X,Y,Z的7Hu矩分量
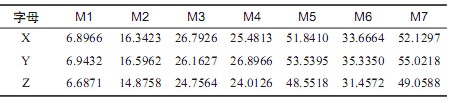
SIFT特征
David G.Lowe在2004年总结了现有的基于不变量技术的特征检测方法,并正式提出了一种基于尺度空间的、对图像缩放、旋转甚至仿射变换保持不变性的图像局部特征描述算子-SIFT算子[6,11],即尺度不变特征变换。
SIFT算法首先在尺度空间进行特征检测,并确定关键点(Keypoints)的位置和关键点所处的尺度,然后使用关键点邻域梯度的主方向作为该点的方向特征,以实现算子对尺度和方向的无关性。
Lowe在图像二维平面空间和DoG(Difference of Gaussian)尺度空间中同时检测局部极值以作为特征点,以使特征具备良好的独特性和稳定性。DoG算子定义为两个不同尺度的高斯核的差分,其具有计算简单的特点,是归一化LoG (Laplacian of Gaussian)算子的近似。DoG算子如下式所示:
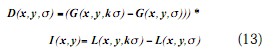
对于图像上的点,计算其在每一尺度下DoG算子的响应值,这些值连起来得到特征尺度轨迹曲线。特征尺度曲线的局部极值点即为该特征的尺度。尺度轨迹曲线上完全可能存在多个局部极值点,这时可认为该点有多个特征尺度。
一幅图像SIFT特征向量的生成算法总共包括4步:
(1)尺度空间极值检测,初步确定关键点位置和所在尺度。
(2)通过拟和三维二次函数以精确确定关键点的位置和尺度,同时去除低对比度的关键点和不稳定的边缘响应点(因为DoG算子会产生较强的边缘响应),以增强匹配稳定性、提高抗噪声能力[6,11]。
(3)利用关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数,使算子具备旋转不变性。
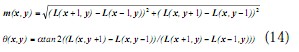
式(14)为(x,y)处梯度的模值和方向公式。其中L所用的尺度为每个关键点各自所在的尺度。
(4)生成SIFT特征向量。 首先将坐标轴旋转为关键点的方向,以确保旋转不变性。接下来以关键点为中心取8×8的窗口。然后在每4×4的小块上计算8个方向的梯度方向直方图,绘制每个梯度方向的累加值,即可形成一个种子点。手语字母图像的SIFT特征提取如图2所示。

图2 (a)手语字母J原图 (b)对(a)提取SIFT特征向量
实验
本文从视频中采集了中国手语字母表中的30个手语字母的图像,30组,每组图像195幅,共5850幅图像作为实验图像。每组的前50幅作为正例训练样本,从其他29组中各选取5幅共145幅作为反例训练样本。每类图像除选作正例的50图像外,剩余的145幅作为测试图像。实验中首先提取图像的7维不变矩特征量,48维Gabor纹理特征,128维SIFT特征作为图像全局和局部特征描述。然后分别采用两种不同核函数(Linear kernel, Radical Basis Function)的SVMs分类器进行训练,对中国手语字母表中的30个手语字母图像的识别结果如表2所示。
表2 30个中国手语字母的识别结果
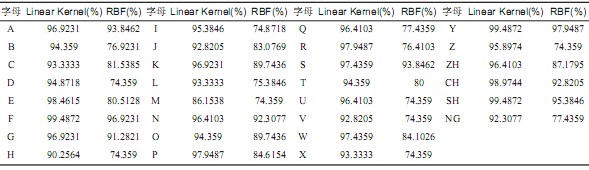
基于线性核函数的SVM平均识别率为95.556%,基于径向基核函数的SVM平均识别率为83.1282%。实验表明,采用径向基核函数的SVM识别率普遍低于采用线性核函数的SVM。
结语
本文提出了一种采用7Hu不变矩特征量等多种图像特征相融合的SVMs手语识别方法。实验表明,在手语识别中,采用图像全局和局部特征相结合的方法,可获得较高的识别率,为手语识别方法的早日推广应用提供了理论依据。
利用矩不变量进行形体识别是模式识别中的一种重要的方法, Hu在1961年首先提出了矩不变量的概念。Hu首先提出代数不变矩的概念,并给出了一组基于通用矩组合的代数矩不变量。这些矩具有平移、尺度和旋转不变性,被称为Hu’s矩。
对于连续灰度函数 f(x, y),它的(p + q)阶二维原点矩Mpq 的定义为:
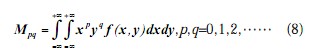
假设 f(x, y)为分段连续的有界函数,并且在x,y平面上有限区域内有非零值。根据唯一性定理,它的各阶矩存在且唯一地被 f(x, y)确定,反过来,f(x, y)也唯一地被它的各阶矩确定。
此外,还可以定义 f(x, y)的(p + q)阶中心矩μpq 为:
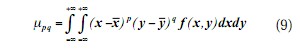
Hu首先提出了不变矩,他给出了连续函数矩的定义和关于矩的基本性质,证明了有关矩的平移不变性、旋转不变性以及比例不变性等性质,具体给出了具有平移不变性、旋转不变性和比例不变性的七个不变矩的表达式。
七个不变矩由二阶和三阶中心矩的线性组合构成,具体表达式如下:

实验中,使用了全部的7Hu不变矩特征量作为手语图像整体形状描述的特征向量。形成特征空间(M1, M2, M3, M4, M5, M6, M7),如表1所示。
表1手语字母X,Y,Z的7Hu矩分量

SIFT特征
David G.Lowe在2004年总结了现有的基于不变量技术的特征检测方法,并正式提出了一种基于尺度空间的、对图像缩放、旋转甚至仿射变换保持不变性的图像局部特征描述算子-SIFT算子[6,11],即尺度不变特征变换。
SIFT算法首先在尺度空间进行特征检测,并确定关键点(Keypoints)的位置和关键点所处的尺度,然后使用关键点邻域梯度的主方向作为该点的方向特征,以实现算子对尺度和方向的无关性。
Lowe在图像二维平面空间和DoG(Difference of Gaussian)尺度空间中同时检测局部极值以作为特征点,以使特征具备良好的独特性和稳定性。DoG算子定义为两个不同尺度的高斯核的差分,其具有计算简单的特点,是归一化LoG (Laplacian of Gaussian)算子的近似。DoG算子如下式所示:
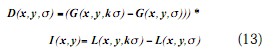
对于图像上的点,计算其在每一尺度下DoG算子的响应值,这些值连起来得到特征尺度轨迹曲线。特征尺度曲线的局部极值点即为该特征的尺度。尺度轨迹曲线上完全可能存在多个局部极值点,这时可认为该点有多个特征尺度。
一幅图像SIFT特征向量的生成算法总共包括4步:
(1)尺度空间极值检测,初步确定关键点位置和所在尺度。
(2)通过拟和三维二次函数以精确确定关键点的位置和尺度,同时去除低对比度的关键点和不稳定的边缘响应点(因为DoG算子会产生较强的边缘响应),以增强匹配稳定性、提高抗噪声能力[6,11]。
(3)利用关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数,使算子具备旋转不变性。
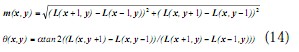
式(14)为(x,y)处梯度的模值和方向公式。其中L所用的尺度为每个关键点各自所在的尺度。
(4)生成SIFT特征向量。 首先将坐标轴旋转为关键点的方向,以确保旋转不变性。接下来以关键点为中心取8×8的窗口。然后在每4×4的小块上计算8个方向的梯度方向直方图,绘制每个梯度方向的累加值,即可形成一个种子点。手语字母图像的SIFT特征提取如图2所示。

图2 (a)手语字母J原图 (b)对(a)提取SIFT特征向量
实验
本文从视频中采集了中国手语字母表中的30个手语字母的图像,30组,每组图像195幅,共5850幅图像作为实验图像。每组的前50幅作为正例训练样本,从其他29组中各选取5幅共145幅作为反例训练样本。每类图像除选作正例的50图像外,剩余的145幅作为测试图像。实验中首先提取图像的7维不变矩特征量,48维Gabor纹理特征,128维SIFT特征作为图像全局和局部特征描述。然后分别采用两种不同核函数(Linear kernel, Radical Basis Function)的SVMs分类器进行训练,对中国手语字母表中的30个手语字母图像的识别结果如表2所示。
表2 30个中国手语字母的识别结果

基于线性核函数的SVM平均识别率为95.556%,基于径向基核函数的SVM平均识别率为83.1282%。实验表明,采用径向基核函数的SVM识别率普遍低于采用线性核函数的SVM。
结语
本文提出了一种采用7Hu不变矩特征量等多种图像特征相融合的SVMs手语识别方法。实验表明,在手语识别中,采用图像全局和局部特征相结合的方法,可获得较高的识别率,为手语识别方法的早日推广应用提供了理论依据。
Linear 相关文章:
- 基于TMS320F2812变频电源的交流采样系统设计(03-22)
- 基于Nios平台的光信号采集片上系统设计(04-04)
- 基于传感器网络技术的深孔测径系统的设计(06-21)
- 基于DSP和FPGA的高精度数据采集卡设计(07-22)
- 基于SRL16E的PN码生成器的设计(08-04)
- PPC405EP在电力监测系统中的应用(08-03)
