基于CPLD的温度自动控制系统的研制
时间:07-24
来源:互联网
点击:
2 温度自动控制系统的软件设计
温度自动控制系统的软件算法通常是根据对象的纯滞后时间τ与对象的惯性时间常数Tm之比来确定,一般来说,当τ/Tmm>0.5时,可采用达林算法控制。在本系统中,针对不同的被控对象,可加载不同的软件算法,因此大大提高了本控制系统的灵活性。由于在工业控制过程中,大量的被控对象具有非线性、纯滞后性,采用PID控制很难获得良好的控制性能,因此本文重点讨论达林算法,用它来控制非线性、纯滞后对象具有良好的效果(被控对象一般为带有滞后的一阶惯性环节)。
2.1 dahlin算法的数学模型
被控对象为带有滞后的一阶惯性环节,其传递函数为
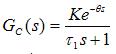
,θ=NT (2-1)
式中:
τ1 -----对象的时间参数
θ -----对象的纯延迟时间,为了简化,设其为采样周期的整数倍,即N为正整数。
K -----对象放大系数
达林算法的设计目标是使整个闭环系统所期望的传递函数Φ(s),相当于一个延时环节和一个惯性环节相串联,即
Φ(s)=

,θ=NT (2-2)
如图6所示,根据控制理论易得到带有一阶惯性对象的达林算法的基本形式:
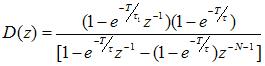
×

(2-3)
式中:
K -----对象放大系数
T ------ 为采样周期;
τ1 ------为被控对象时间参数;
τ ------为闭环系统的时间参数。
根据D(Z)=U(Z)/E(Z)得出差分方程:
U(K)=b1U(K-1)+b2U(K-N-1)+a0E(K)-a1E(K-1) (2-4)
其中
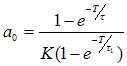
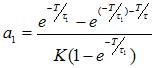
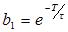
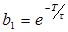
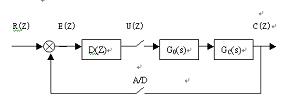
图6 控制系统方框图
2.2 dahlin算法参数的整定
(1)由系统的飞升曲线(如图7)确定对象的纯滞后时间参数θ和被控对象的时间参数τ1。

图7 被控对象的飞升曲线
(2)综合控制精度、超调量等指标选取合适的采样周期T。若T偏大,则取样稀疏,单位时间内控制点过少,势必造成较大的过冲量以及系统控制误差;若T偏小,则对采样量化字长要求过高,对于有限字长的控制系统过密的采样周期会使系统控制失败。
(3)由N=θ/T确定N值。
(4)对象放大系数K的确定。K可由下列公式确定:

(5)τ一般与T取同量级,不断调整τ值,观察系统的响应图,使得闭环系统的指标达到最佳。
3 系统应用
从该温度自动控制系统的软硬件构成可以看出,这种设计具有比较好的开放性,便于在软硬件方面进行功能扩展和重新配置,同时应用系统的构造也比较灵活。由于采用了高容量低成本的CPLD器件 MAX7128,将本系统的控制部分的核心电路的硬件资源进行了整合集成,提高了系统硬件的可靠性。针对不同的控制对象,只要适当的改变一下前端的信号处理电路,并采用满足要求的控制算法,即可胜任面对各种对象的控制任务。因此系统具备结构开放、性能可靠、灵活方便等特点,可以灵活地胜任不同对象的温度自动控制任务。
温度自动控制系统的软件算法通常是根据对象的纯滞后时间τ与对象的惯性时间常数Tm之比来确定,一般来说,当τ/Tmm>0.5时,可采用达林算法控制。在本系统中,针对不同的被控对象,可加载不同的软件算法,因此大大提高了本控制系统的灵活性。由于在工业控制过程中,大量的被控对象具有非线性、纯滞后性,采用PID控制很难获得良好的控制性能,因此本文重点讨论达林算法,用它来控制非线性、纯滞后对象具有良好的效果(被控对象一般为带有滞后的一阶惯性环节)。
2.1 dahlin算法的数学模型
被控对象为带有滞后的一阶惯性环节,其传递函数为
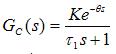
,θ=NT (2-1)
式中:
τ1 -----对象的时间参数
θ -----对象的纯延迟时间,为了简化,设其为采样周期的整数倍,即N为正整数。
K -----对象放大系数
达林算法的设计目标是使整个闭环系统所期望的传递函数Φ(s),相当于一个延时环节和一个惯性环节相串联,即
Φ(s)=

,θ=NT (2-2)
如图6所示,根据控制理论易得到带有一阶惯性对象的达林算法的基本形式:
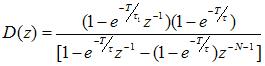
×

(2-3)
式中:
K -----对象放大系数
T ------ 为采样周期;
τ1 ------为被控对象时间参数;
τ ------为闭环系统的时间参数。
根据D(Z)=U(Z)/E(Z)得出差分方程:
U(K)=b1U(K-1)+b2U(K-N-1)+a0E(K)-a1E(K-1) (2-4)
其中
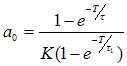
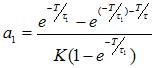
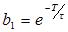
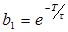

图6 控制系统方框图
2.2 dahlin算法参数的整定
(1)由系统的飞升曲线(如图7)确定对象的纯滞后时间参数θ和被控对象的时间参数τ1。

图7 被控对象的飞升曲线
(2)综合控制精度、超调量等指标选取合适的采样周期T。若T偏大,则取样稀疏,单位时间内控制点过少,势必造成较大的过冲量以及系统控制误差;若T偏小,则对采样量化字长要求过高,对于有限字长的控制系统过密的采样周期会使系统控制失败。
(3)由N=θ/T确定N值。
(4)对象放大系数K的确定。K可由下列公式确定:

(5)τ一般与T取同量级,不断调整τ值,观察系统的响应图,使得闭环系统的指标达到最佳。
3 系统应用
从该温度自动控制系统的软硬件构成可以看出,这种设计具有比较好的开放性,便于在软硬件方面进行功能扩展和重新配置,同时应用系统的构造也比较灵活。由于采用了高容量低成本的CPLD器件 MAX7128,将本系统的控制部分的核心电路的硬件资源进行了整合集成,提高了系统硬件的可靠性。针对不同的控制对象,只要适当的改变一下前端的信号处理电路,并采用满足要求的控制算法,即可胜任面对各种对象的控制任务。因此系统具备结构开放、性能可靠、灵活方便等特点,可以灵活地胜任不同对象的温度自动控制任务。
CPLD 单片机 电路 传感器 51单片机 电压 放大器 电路图 总线 CMOS 可控硅 变压器 比较器 相关文章:
- 基于DSP高精度伺服位置环设计(06-21)
- 双目三维定位的视频运动检测控制系统设计(01-21)
- 图像采集系统的Camera Link标准接口设计(01-16)
- 激光微加工系统及基于DSP+FPGA的控制单元的研究(03-05)
- 基于USB2.0技术的高速双路数据采集系统(03-07)
- 基于MATLAB用于谐波检测的数字低通滤波器的设计(03-11)
