基于有限状态机的自动售货机控制器
时间:03-29
来源:互联网
点击:
引言
售货机上除基本自动售货功能外,增加了诸多功能,如GPRS短信模块以加强安全监控,在售货机上播放视频广告以提高运营商的经济效益等。这就使得存在于售货机内部的控制器(Vencling Machine Controller,VMC)的复杂程度也迅速增加,先前的一套用于小规模嵌入式系统的分析设计方法、应用程序结构、运行效率与易维护程度在当前的售货机需求面前显得有些力不从心了。有限状态机理论在计算机应用领域有着广泛的应用,状态机对处理一些复杂情况也大有裨益。在设计阶段,开发人员可以利用状态机模型来描述复杂的系统,从而大大缩短项目的开发周期,且系统易于维护。魏先民提出了有限状态机在嵌入式领域应用的一个基本框架,但是在这个框架中,系统中的所有状态都是互斥的关系,尽管有些状态之间存在着紧密的关系。V.Ayvazyan等论述了状态之间不仅存在互斥关系,还存在包含关系(父状态与子状态)。本文应用有限状态机的这些特性,提出一个层次型有限状态机(Hierarchical FSM,HFSM)模型,对售货机控制器(VMC)进行改进。
1 有限状态机
有限状态机是一种具有离散输入输出系统的模型,在任何时刻都处于一个特定的状态。对于事件驱动的程序设计,它是非常有用的设计模型。在某一个状态下有事件发生时,根据当前状态和输入事件的不同,选择如何处理该事件以及是否需要转换到下一个状态。一个有限状态机(FSM)是一个五元组,M=(K,E,T,S,Z)。其中,K是一个有限的状态集合,它的每个元素称为“状态”;E表示该系统能接收的所有事件的集合,它的每个元素称为一个“事件”;T是状态转换函数,是K×E→K上的映射;S 是系统的一个特殊状态,一般是系统启动时的初始状态;Z是K的一个子集,是一个终态集。
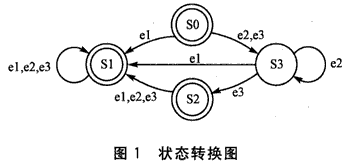
有限状态机一般有2种表示方式:状态转移表和状态转移图。通常用有向图来表示有限状态机,其节点代表状态。如图1所示,若在状态SO接收到某个输入事件 e1后转向S1状态,就在图中画一条从SO到Sl的带箭头的弧线,并在弧线上标记e1。
2 基本思想
2.1 必要性分析
有限状态机是通过事件来触发状态的转变的,其事件来源主要有2个:其一是外部触发事件,如响应用户键盘的输入;其二是内部触发事件,如系统所发出来的各种命令。有限状态机这种事件驱动的特性具有良好的开放性,可以根据用户的要求方便地增加相应的状态与事件,完成系统功能的扩展。本文所研究的自动售货机配有1个5×5的管理键盘和1个3×7用户键盘,二者复用了部分的键盘扫描线;另外有37个外部事件源,加上几条内部命令,可能触发的事件达45 个。如此多的事件,当某个事件发生时,如果采用if…else或switch…case语句进行一一判断,将非常复杂。而采用有限状态机,每个状态维护一张事件表,无需比较,大大提高了响应速度;并且就扩展需求较为频繁的自动售货机而言,有限状态机也是便于维护的。
2.2 实现方式
根据系统中各个状态之间是否存在包含关系,有限状态机可以分为常规状态机与层次型状态机(hierarchicalstate machine)。对于前者,系统中各个状态是独立的、互斥的,适合应用于那些存在状态数量不多的简单系统;而对于后者,系统中的状态除了互斥关系以外,还存在真包含的关系。
分析自动售货机这样一个状态机,图2为自动售货机的状态图(不完整)。
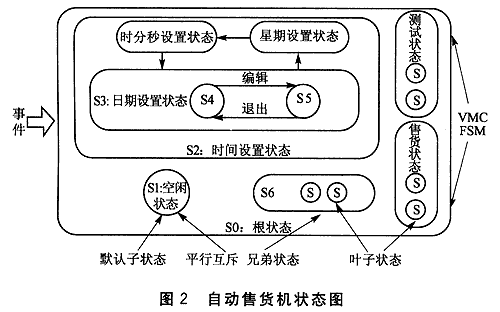
从图中可以看出,自动售货机控制器存在的状态数量是比较多的,但是无论何时,自动售货机总处于空闲、售货、商品价格设置、时间设置、测试等诸多状态之中的一个.这些状态之间是互斥的。同时,上面列举的所有状态都包含子状态,例如:状态S2(时间设置状态)包括日期设置、时分秒设置、星期设置等子状态,而对于S3(日期设置状态)又包括S4(日期显示状态)和S5(日期编辑状态)两个子状态。因此,对于自动售货机控制器这样一个系统,其内部的状态机是一种层次型状态机。本文根据层次型状态机的互斥与包含的双重特性,提出层次型有限状态机模型,并且用来实现自动售货机控制器。模型使用树结构来描述状态集,包含其他状态的状态称为“树枝节点”,不包含其他状态的状态称为“叶子节点”。为方便用单树结构描述,总是设计一个状态包含所有的状态节点,称为“根节点”,它是一个虚拟的节点,在系统中没有状态与其对应。状态机只能停留在叶子节点,而不能停留在树枝节点,每个树枝节点需指定一个子节点为它的默认子节点,以便状态机进入树枝节点时能停留到叶子节点。
3 层次型有限状态机模型
3.1 数据结构定义
HFSM模型采用树结构实现有限状态机,树上的每一个节点都对应了自动售货机状态机的一个状态。其中根节点是一个特殊的节点,它对应的是一个虚拟的并不存在的状态,其目的是为了构造一棵单树,而不是每一个功能对应一棵树。节点的数据结构如下:

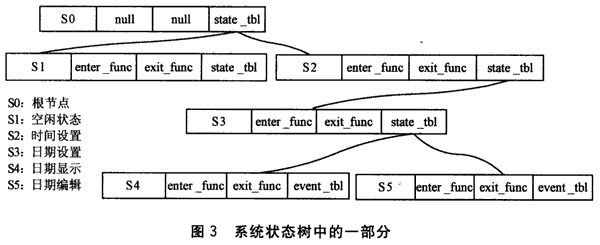
其中,id为状态编号,每个状态编号在整个系统状态机中是唯一的;name为状态名;enter_func为状态进入操作;exit_func为状态退出操作;event_table为事件表;sub_state_table为子状态表。因为叶子节点没有子状态,而树枝节点没有状态事件表,所以结构中的事件表与子状态可以共享一段存储空间。事件表中每个元素是另外一个结构FSM_STATE_EVENT,它有事件id(与事件源一一对应)、事件操作 (func)和下一状态编号(next_state_id)三个成员。图2所示的状态图子集经过处理形成图3所示的状态树,它是整个自动售货机状态树的一部分。
3.2 状态转换算法
在有限状态机中,是通过事件的驱动而进行状态转换的。状态转换算法的关键就在于查找下一状态在状态树中的位置,也就是在状态树中查找下一状态的时间复杂度的问题。与常规状态机不同,层次型状态机中的各个状态不仅存在互斥关系,还存在包含关系,特别是当前状态与下一状态关系就更为紧密了,不仅存在局部相关性,而且在很多情况下,它们之间在状态树中表现为兄弟节点关系。因此,要在状态树查找下一状态,需先查找当前节点的兄弟节点,再查找父节点的兄弟节点。如此循环,直到找到下一状态或试图查找根节点的兄弟节点(根节点没有父节点,所以要查找的下一状态是不存在的)。
状态查找算法如下:

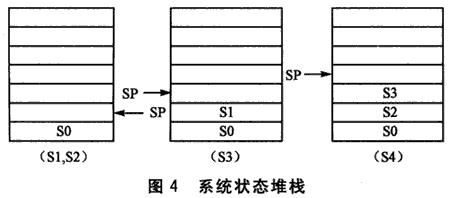
有限状态机的一般状态转换过程是:系统首先执行exit_func退出当前状态,然后执行驱动此次状态转换的事件操作func,最后执行 enter_func进入新状态。为了便于遍历状态树,系统为层次型有限状态机建立一个状态堆栈,堆栈中记录的数据是当前状态在状态树中对应的节点路径上所有节点(自身除外,因为没有必要人栈)的地址。堆栈的初始状态如图4所示,此时系统处于空闲S1状态,栈中只有根节点信息。在某个事件或一系列事件的驱动下(比如通过按键显示系统的当前日期),系统将要从空闲状态转换到日期显示状态S4。从图3的自动售货机状态树可以看出,系统需要经过S1一S2一S3 一S4的过程,中间的S2和S3是不可停留的状态。当按下管理键盘的“Time”键时,系统先执行exit_idle函数退出S1(空闲状态),然后根据空闲状态的事件表得到下一状态编号,再通过状态查找算法搜索状态树,最后到达目的状态S4。S2与S3是两个中间状态,但是这两个状态节点的地址需要入栈。
3.3 模型评价
(1)扩展性
为层次型有限状态机模型增加新功能,只需在其根节点下增加一个子节点,因为新的子节点与其他兄弟节点是互斥的,所以模型可以很方便地进行系统功能扩展。
(2)查找算法时间复杂度
假设系统中存在的状态数量为n。如果不采用层次型有限状态机模型,那么系统中的各个状态都是相互独立、互斥的,相当于所有的状态都是一个虚拟根节点的子节点。这样的话,查找下一状态的时间复杂度为:

然而,上面的情况忽略了状态之间的相关性,很有可能当前状态与下一状态是兄弟关系,此时的比较次数就会明显减少。如果采用层次型状态机,假设系统子功能数目为m(m>1),那么平均每个子功能的状态数目为n/m,当前状态与下一状态为兄弟节点的概率为p(0<p<1)。这种情况下的时间复杂度为:
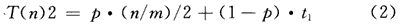
其中,t1为当前状态与下一状态不是兄弟节点的查找时间,与状态树的平均深度^有关。但是由于存在局部相关性,并且这种相关性越大(即p值越大),平均时间复杂度就越集中在前面部分(p·n)/(m·2),后面的表达式值可以忽略不计,即:
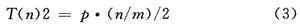
显然,T(n)2<T(n)1。因此,该模型对于查找下一状态在时间复杂度上也是有优势的。
售货机上除基本自动售货功能外,增加了诸多功能,如GPRS短信模块以加强安全监控,在售货机上播放视频广告以提高运营商的经济效益等。这就使得存在于售货机内部的控制器(Vencling Machine Controller,VMC)的复杂程度也迅速增加,先前的一套用于小规模嵌入式系统的分析设计方法、应用程序结构、运行效率与易维护程度在当前的售货机需求面前显得有些力不从心了。有限状态机理论在计算机应用领域有着广泛的应用,状态机对处理一些复杂情况也大有裨益。在设计阶段,开发人员可以利用状态机模型来描述复杂的系统,从而大大缩短项目的开发周期,且系统易于维护。魏先民提出了有限状态机在嵌入式领域应用的一个基本框架,但是在这个框架中,系统中的所有状态都是互斥的关系,尽管有些状态之间存在着紧密的关系。V.Ayvazyan等论述了状态之间不仅存在互斥关系,还存在包含关系(父状态与子状态)。本文应用有限状态机的这些特性,提出一个层次型有限状态机(Hierarchical FSM,HFSM)模型,对售货机控制器(VMC)进行改进。
1 有限状态机
有限状态机是一种具有离散输入输出系统的模型,在任何时刻都处于一个特定的状态。对于事件驱动的程序设计,它是非常有用的设计模型。在某一个状态下有事件发生时,根据当前状态和输入事件的不同,选择如何处理该事件以及是否需要转换到下一个状态。一个有限状态机(FSM)是一个五元组,M=(K,E,T,S,Z)。其中,K是一个有限的状态集合,它的每个元素称为“状态”;E表示该系统能接收的所有事件的集合,它的每个元素称为一个“事件”;T是状态转换函数,是K×E→K上的映射;S 是系统的一个特殊状态,一般是系统启动时的初始状态;Z是K的一个子集,是一个终态集。
有限状态机一般有2种表示方式:状态转移表和状态转移图。通常用有向图来表示有限状态机,其节点代表状态。如图1所示,若在状态SO接收到某个输入事件 e1后转向S1状态,就在图中画一条从SO到Sl的带箭头的弧线,并在弧线上标记e1。

2 基本思想
2.1 必要性分析
有限状态机是通过事件来触发状态的转变的,其事件来源主要有2个:其一是外部触发事件,如响应用户键盘的输入;其二是内部触发事件,如系统所发出来的各种命令。有限状态机这种事件驱动的特性具有良好的开放性,可以根据用户的要求方便地增加相应的状态与事件,完成系统功能的扩展。本文所研究的自动售货机配有1个5×5的管理键盘和1个3×7用户键盘,二者复用了部分的键盘扫描线;另外有37个外部事件源,加上几条内部命令,可能触发的事件达45 个。如此多的事件,当某个事件发生时,如果采用if…else或switch…case语句进行一一判断,将非常复杂。而采用有限状态机,每个状态维护一张事件表,无需比较,大大提高了响应速度;并且就扩展需求较为频繁的自动售货机而言,有限状态机也是便于维护的。
2.2 实现方式
根据系统中各个状态之间是否存在包含关系,有限状态机可以分为常规状态机与层次型状态机(hierarchicalstate machine)。对于前者,系统中各个状态是独立的、互斥的,适合应用于那些存在状态数量不多的简单系统;而对于后者,系统中的状态除了互斥关系以外,还存在真包含的关系。
分析自动售货机这样一个状态机,图2为自动售货机的状态图(不完整)。

从图中可以看出,自动售货机控制器存在的状态数量是比较多的,但是无论何时,自动售货机总处于空闲、售货、商品价格设置、时间设置、测试等诸多状态之中的一个.这些状态之间是互斥的。同时,上面列举的所有状态都包含子状态,例如:状态S2(时间设置状态)包括日期设置、时分秒设置、星期设置等子状态,而对于S3(日期设置状态)又包括S4(日期显示状态)和S5(日期编辑状态)两个子状态。因此,对于自动售货机控制器这样一个系统,其内部的状态机是一种层次型状态机。本文根据层次型状态机的互斥与包含的双重特性,提出层次型有限状态机模型,并且用来实现自动售货机控制器。模型使用树结构来描述状态集,包含其他状态的状态称为“树枝节点”,不包含其他状态的状态称为“叶子节点”。为方便用单树结构描述,总是设计一个状态包含所有的状态节点,称为“根节点”,它是一个虚拟的节点,在系统中没有状态与其对应。状态机只能停留在叶子节点,而不能停留在树枝节点,每个树枝节点需指定一个子节点为它的默认子节点,以便状态机进入树枝节点时能停留到叶子节点。
3 层次型有限状态机模型
3.1 数据结构定义
HFSM模型采用树结构实现有限状态机,树上的每一个节点都对应了自动售货机状态机的一个状态。其中根节点是一个特殊的节点,它对应的是一个虚拟的并不存在的状态,其目的是为了构造一棵单树,而不是每一个功能对应一棵树。节点的数据结构如下:

其中,id为状态编号,每个状态编号在整个系统状态机中是唯一的;name为状态名;enter_func为状态进入操作;exit_func为状态退出操作;event_table为事件表;sub_state_table为子状态表。因为叶子节点没有子状态,而树枝节点没有状态事件表,所以结构中的事件表与子状态可以共享一段存储空间。事件表中每个元素是另外一个结构FSM_STATE_EVENT,它有事件id(与事件源一一对应)、事件操作 (func)和下一状态编号(next_state_id)三个成员。图2所示的状态图子集经过处理形成图3所示的状态树,它是整个自动售货机状态树的一部分。

3.2 状态转换算法
在有限状态机中,是通过事件的驱动而进行状态转换的。状态转换算法的关键就在于查找下一状态在状态树中的位置,也就是在状态树中查找下一状态的时间复杂度的问题。与常规状态机不同,层次型状态机中的各个状态不仅存在互斥关系,还存在包含关系,特别是当前状态与下一状态关系就更为紧密了,不仅存在局部相关性,而且在很多情况下,它们之间在状态树中表现为兄弟节点关系。因此,要在状态树查找下一状态,需先查找当前节点的兄弟节点,再查找父节点的兄弟节点。如此循环,直到找到下一状态或试图查找根节点的兄弟节点(根节点没有父节点,所以要查找的下一状态是不存在的)。
状态查找算法如下:

有限状态机的一般状态转换过程是:系统首先执行exit_func退出当前状态,然后执行驱动此次状态转换的事件操作func,最后执行 enter_func进入新状态。为了便于遍历状态树,系统为层次型有限状态机建立一个状态堆栈,堆栈中记录的数据是当前状态在状态树中对应的节点路径上所有节点(自身除外,因为没有必要人栈)的地址。堆栈的初始状态如图4所示,此时系统处于空闲S1状态,栈中只有根节点信息。在某个事件或一系列事件的驱动下(比如通过按键显示系统的当前日期),系统将要从空闲状态转换到日期显示状态S4。从图3的自动售货机状态树可以看出,系统需要经过S1一S2一S3 一S4的过程,中间的S2和S3是不可停留的状态。当按下管理键盘的“Time”键时,系统先执行exit_idle函数退出S1(空闲状态),然后根据空闲状态的事件表得到下一状态编号,再通过状态查找算法搜索状态树,最后到达目的状态S4。S2与S3是两个中间状态,但是这两个状态节点的地址需要入栈。

3.3 模型评价
(1)扩展性
为层次型有限状态机模型增加新功能,只需在其根节点下增加一个子节点,因为新的子节点与其他兄弟节点是互斥的,所以模型可以很方便地进行系统功能扩展。
(2)查找算法时间复杂度
假设系统中存在的状态数量为n。如果不采用层次型有限状态机模型,那么系统中的各个状态都是相互独立、互斥的,相当于所有的状态都是一个虚拟根节点的子节点。这样的话,查找下一状态的时间复杂度为:

然而,上面的情况忽略了状态之间的相关性,很有可能当前状态与下一状态是兄弟关系,此时的比较次数就会明显减少。如果采用层次型状态机,假设系统子功能数目为m(m>1),那么平均每个子功能的状态数目为n/m,当前状态与下一状态为兄弟节点的概率为p(0<p<1)。这种情况下的时间复杂度为:
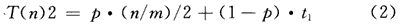
其中,t1为当前状态与下一状态不是兄弟节点的查找时间,与状态树的平均深度^有关。但是由于存在局部相关性,并且这种相关性越大(即p值越大),平均时间复杂度就越集中在前面部分(p·n)/(m·2),后面的表达式值可以忽略不计,即:
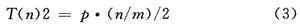
显然,T(n)2<T(n)1。因此,该模型对于查找下一状态在时间复杂度上也是有优势的。
- 基于ARM与DSP的嵌入式运动控制器设计(04-25)
- 多核及虚拟化技术在工业和安全领域的应用(05-23)
- 基于ARM核的AT75C220及其在指纹识别系统中的应用(05-24)
- 基于FPGA安全封装的身份认证模型研究(05-27)
- 基于nRF2401智能无线火灾监控系统设计(04-01)
- 智能视频多媒体技术的应用(05-31)
