DSP滤波器用于扩展数字化仪器性能分析
时间:09-25
来源:互联网
点击:
DSP滤波器的应用范围
DSP在数字化测量系统中有多种功能获得广泛采用,它们可改善有限取样率引起的频率响应、相位响应、噪声性能、带宽扩展等指标。
数字化测量系统(如数字化仪、数字示波器)的DSP配置如图1所示,DSP对A/D转换后的模拟信号数据流进行数字处理,最常用的功能有快速傅立叶变换(FFT)、数字调制、增益控制、编码/解码等在数字通信中广为人知的运算,而在数字化测量系统中最重要的功能是数字滤波器,DSP滤波器作为软件滤波器能够提供比硬件滤波器更优异的特性。数字化测量系统对被测波形的数学运算即可使用有限冲激响应(FIR)滤波器,亦可使用无限冲激响应(IIR)滤波器,DSP滤波器可视为一种修改波形形状的数学程序。根据要求我们可设计出特定的滤波器,把波形变换成所希望的任何形状。因为从广义上来看,处理信号的任何系统都可视为滤滤器,以数字示波器为例,它的DC输入通道是低通滤波器,3dB滚降点就是它的频率带宽,在AC输入情况下它就是带通滤波器。DSP滤波器的主要应用如下:
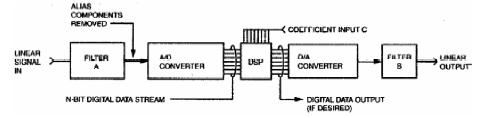
DSP滤波器用于扩展数字化仪器
波形重建
数字示滤器受A/D转换器取样率的限制,波形的取样点是有限的和非连续的,为了便于观察,必须对变换后的离散样点作波形重建,亦即在样点之间添加数据点,使数字化后的波形具有更好的可视性和测量精度。在实时数字示波器中,对被测信号只有单次数据采集,采用软件波形重建是唯一的选择。
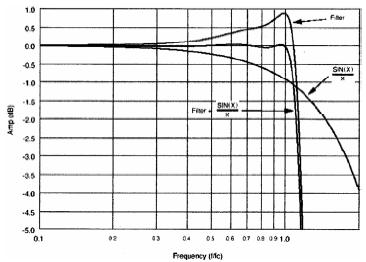
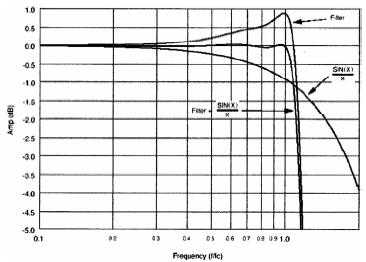
最简单的波形重建是线性内插滤波器,显然将两取样点作直线连接后的重建波形不够平滑,在波形突变段的可视性更差。更精确的波形重建采用Sinx函数的内插滤波器,Sin(x)/X内插滤波器可获得平滑的波形重建和更准确的绝对值,而且不会引入混淆频率。根据取样原理,定义取样频率fs=2fN,fN是奈奎斯特频率,亦即fN是数字化后的最高频率,需要采用砖墙型滤波器抑制fN以上频率,否则将引入混淆频率,产生不可接受的测量误差。例如数字示滤器采用20GS/s的取样率的,fN等于10GHz。为了保证获得最高10GHz的带宽,必须采用10GHz的砖墙型硬件滤波器。如图2所示,红线(右)表示10GHz的fN砖墙型滤波器,这种理论滤波器实际上无法用硬件来实现的。传统上模拟示波器采用高斯型滚降特性,用绿线(左)表示的-3dB带宽是5GHz,由于滚降曲线的下降段非常缓慢,在-3dB点后面还有超过奈奎斯特频率的高频分量,如图中斜线部分所示。因此,数字示波器不采用高斯响应滤波器而采用最大平滑响应滤波器,用篮线(中)表示的-3dB带宽达到8GHz。这种高防最大平滑响应滤波器使数字示波器的带宽接近奈奎斯特频率,在A/D转换器的取样率是20GS/s下,通过Sin(x)/x滤波器使波形重建和DSP滤波处理后,可获得8GHz的-3dB带宽。亦即,采用Sin(x)/x滤波器的波形重建能够获得0.4倍取样频率fs的带宽。
DSP滤波器用于扩展数字化仪器
幅度平滑
数字化测量系统由于硬件的不均匀性,导导致频率特性在通带内不够平滑,数字示波器的频率响应特性曲线在低频段具有一致的幅度,然后进入高频的滚降段,如图2的绿线所示。实际上,频率响应曲线在中频段开始变差,在某些频点上硬体会衰减或建峰信号,特别是接近带宽限值时出现频率响应的异常峰值。按照频率带宽的定义,只提及-3dB滚降点,故电路设计工程师为了扩展带宽,在高频段加入建峰补偿。图3是某种数字示波器的实测频率响应曲线,红线(上)表明具有6GHz的实时带宽,但同时可见在3.5GHz和5.5GHz分别出现+1dB和+2dB的建峰响应。由于示波器供应商不提供频率响应的不平整度数据,只按-3dB确定实时带宽,这样必然引入幅度测量的严重误差。
DSP滤波器用于扩展数字化仪器
采用DSP幅度平滑滤波器能够明显改善数字示波器的频率响应幅度误差,篮线(下)是修正后的频率响应,幅度偏差控制在±1dB以内,带宽仍然保持6GHz,而原来从3 GHz至5 GHz的建峰得到平滑。这种从硬件滤波器达到使频率响应建峰,再从软件滤波器使频率响应平滑,对具有高取样率的数字示波器来说,它是十分有效的硬件/软件相结合的扩展带宽和提高幅度平整度的方法。
相位校正
数字信号通常由基波和大量谐波组成,数字测量系统除了保证被测信号的幅度—频率响应之外,对于相位—频率响应亦不应引入相位延迟。由于数字示波器的硬件往往使高频谐波产生相移,结果是信号的群延迟增加。为了消除群延迟导致信号失真,只有提高仪器的带宽或由DSP滤波器作相位校正,显然后者是最经济有效的办法。借助与幅度平整使用的FIR滤波器的相似设计,不难使重建波形的群延减小,使被测高速数字波形的瞬态失真保持在最低限值以内。
DSP在数字化测量系统中有多种功能获得广泛采用,它们可改善有限取样率引起的频率响应、相位响应、噪声性能、带宽扩展等指标。
数字化测量系统(如数字化仪、数字示波器)的DSP配置如图1所示,DSP对A/D转换后的模拟信号数据流进行数字处理,最常用的功能有快速傅立叶变换(FFT)、数字调制、增益控制、编码/解码等在数字通信中广为人知的运算,而在数字化测量系统中最重要的功能是数字滤波器,DSP滤波器作为软件滤波器能够提供比硬件滤波器更优异的特性。数字化测量系统对被测波形的数学运算即可使用有限冲激响应(FIR)滤波器,亦可使用无限冲激响应(IIR)滤波器,DSP滤波器可视为一种修改波形形状的数学程序。根据要求我们可设计出特定的滤波器,把波形变换成所希望的任何形状。因为从广义上来看,处理信号的任何系统都可视为滤滤器,以数字示波器为例,它的DC输入通道是低通滤波器,3dB滚降点就是它的频率带宽,在AC输入情况下它就是带通滤波器。DSP滤波器的主要应用如下:

DSP滤波器用于扩展数字化仪器
波形重建
数字示滤器受A/D转换器取样率的限制,波形的取样点是有限的和非连续的,为了便于观察,必须对变换后的离散样点作波形重建,亦即在样点之间添加数据点,使数字化后的波形具有更好的可视性和测量精度。在实时数字示波器中,对被测信号只有单次数据采集,采用软件波形重建是唯一的选择。
最简单的波形重建是线性内插滤波器,显然将两取样点作直线连接后的重建波形不够平滑,在波形突变段的可视性更差。更精确的波形重建采用Sinx函数的内插滤波器,Sin(x)/X内插滤波器可获得平滑的波形重建和更准确的绝对值,而且不会引入混淆频率。根据取样原理,定义取样频率fs=2fN,fN是奈奎斯特频率,亦即fN是数字化后的最高频率,需要采用砖墙型滤波器抑制fN以上频率,否则将引入混淆频率,产生不可接受的测量误差。例如数字示滤器采用20GS/s的取样率的,fN等于10GHz。为了保证获得最高10GHz的带宽,必须采用10GHz的砖墙型硬件滤波器。如图2所示,红线(右)表示10GHz的fN砖墙型滤波器,这种理论滤波器实际上无法用硬件来实现的。传统上模拟示波器采用高斯型滚降特性,用绿线(左)表示的-3dB带宽是5GHz,由于滚降曲线的下降段非常缓慢,在-3dB点后面还有超过奈奎斯特频率的高频分量,如图中斜线部分所示。因此,数字示波器不采用高斯响应滤波器而采用最大平滑响应滤波器,用篮线(中)表示的-3dB带宽达到8GHz。这种高防最大平滑响应滤波器使数字示波器的带宽接近奈奎斯特频率,在A/D转换器的取样率是20GS/s下,通过Sin(x)/x滤波器使波形重建和DSP滤波处理后,可获得8GHz的-3dB带宽。亦即,采用Sin(x)/x滤波器的波形重建能够获得0.4倍取样频率fs的带宽。

DSP滤波器用于扩展数字化仪器
幅度平滑
数字化测量系统由于硬件的不均匀性,导导致频率特性在通带内不够平滑,数字示波器的频率响应特性曲线在低频段具有一致的幅度,然后进入高频的滚降段,如图2的绿线所示。实际上,频率响应曲线在中频段开始变差,在某些频点上硬体会衰减或建峰信号,特别是接近带宽限值时出现频率响应的异常峰值。按照频率带宽的定义,只提及-3dB滚降点,故电路设计工程师为了扩展带宽,在高频段加入建峰补偿。图3是某种数字示波器的实测频率响应曲线,红线(上)表明具有6GHz的实时带宽,但同时可见在3.5GHz和5.5GHz分别出现+1dB和+2dB的建峰响应。由于示波器供应商不提供频率响应的不平整度数据,只按-3dB确定实时带宽,这样必然引入幅度测量的严重误差。

DSP滤波器用于扩展数字化仪器
采用DSP幅度平滑滤波器能够明显改善数字示波器的频率响应幅度误差,篮线(下)是修正后的频率响应,幅度偏差控制在±1dB以内,带宽仍然保持6GHz,而原来从3 GHz至5 GHz的建峰得到平滑。这种从硬件滤波器达到使频率响应建峰,再从软件滤波器使频率响应平滑,对具有高取样率的数字示波器来说,它是十分有效的硬件/软件相结合的扩展带宽和提高幅度平整度的方法。
相位校正
数字信号通常由基波和大量谐波组成,数字测量系统除了保证被测信号的幅度—频率响应之外,对于相位—频率响应亦不应引入相位延迟。由于数字示波器的硬件往往使高频谐波产生相移,结果是信号的群延迟增加。为了消除群延迟导致信号失真,只有提高仪器的带宽或由DSP滤波器作相位校正,显然后者是最经济有效的办法。借助与幅度平整使用的FIR滤波器的相似设计,不难使重建波形的群延减小,使被测高速数字波形的瞬态失真保持在最低限值以内。
DSP 滤波器 示波器 低通滤波器 电路 安捷伦 频谱分析仪 二极管 放大器 泰克 电压 模拟前端 电子 数字电视 相关文章:
- F1aSh存储器在TMS320C3X系统中的应用(11-11)
- 基于PIC18F系列单片机的嵌入式系统设计(11-19)
- DSP在卫星测控多波束系统中的应用(01-25)
- 基于PCI总线的双DSP系统及WDM驱动程序设计(01-26)
- 利用Virtex-5 FPGA实现更高性能的方法(03-08)
- DSP与单片机通信的多种方案设计(03-08)
