基于声卡的QPSK信号的实时软解调

引言

目前，调制解调器产品大都采用专用DSP芯片作为核心处理器件，这是因为DSP是专门的数字信号处理芯片，其处理速度快，实时性好。但另一方面，也存在一些弊端，如开发周期长、价格昂贵，不能存入和读取数据，必须要与PC机配合使用等。近几年来，PC机的各项技术得到了迅速发展，CPU的计算速度、内存容量都大幅度提高，其数字信号处理能力已经完全可以满足对常规通信信号的实时解调。将调制解调器设计在声卡上而不是DSP芯片上，有很多好处：首先，声卡廉价易得，充分利用卡上的line in、mic in、line out、spk out等端口，可以实现多路信号的实时解调，一卡多用；其次，优化后的解调软件占用CPU的时间很少，可以在接收数据的同时从事其他工作；第三，不受存储空间的限制，用高级语言编程，设计周期短。另外，这种设计方案与硬件平台无关，软件升级周期短。本文正是基于这种思想，抛开DSP器件，以PC机为硬件平台，实现对QPSK信号的实时解调，系统框图如图1所示。



图1中，接收机输出的基带信号经PC机声卡采样后得到离散化的数字序列。对信号的采样可调用Windows的API函数对声卡进行控制，包括采样频率、缓存大小、每次读入的字节数等，具体实现可参看相关资料，本文不再赘述。图1中的解调软件部分是本文讨论的重点，它完成对信号的数字化实时解调功能，其数字化解调原理如图2所示。



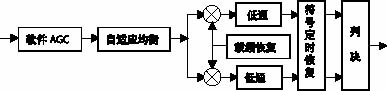
软件AGC

软件AGC用于跟踪信号外包络变化实现对衰落的补偿。本文采用图3所示对数AGC。



图3中的对数AGC用软件实现时，A(n)的计算采用下式。

log{A(n+1)}=log{A(n)}+α[log{R}-log{｜A(n)x(n)｜}]

图中，x(n)是软件AGC的输入信号，y(n)是输出信号；A(n)是AGC的增益控制变量；α和R为常量，取值根据设计要求在补偿速度和稳定性之间取折中，当要求补偿速度迅速时，取较大的值，反之，取较小的值。

DFPLL载波频率恢复

在位同步点附近，存在信号的码间串扰问题。DFPLL的基本思想就是，对于每个码元，利用位同步附近的采样点计算码元的相位，并根据基带信号码元的相位特点，计算出参考载波与信号载波的差值，利用此差值调整VCO的相位，进行载波恢复。

设QPSK信号的第n个码元在位同步点处的相位信息为：，其中，i=0,1,2,3,θ(n)为第n个码元的相位偏移。要得到相位误差，需要去除相位信息中的信息分量πi/2，通过观察QPSK星座图可以发现，相邻星座点间的相差总在π/2附近，于是用如下方法可以去除信息分量。令，并令，其中，mod表示求余，ξ(n)是单个码元的相位误差。如果采样频率为Fs，码元速率为fb，则该码元每个采样点的平均相位误差为e(n)=ξ(n)/(Fs/fb)。平均相位误差送入环路滤波器，滤波结果由系数k调整后，送入VCO进行相位增量调整，当e(n)稳定在一个较小值附近时，DFPLL处于锁定状态。环路滤波器采用一阶RC低通滤波器。由于其输入为相位估计器，考虑来自相位估计器的相位差值信号以码元速率fb变化，其截止频率应在fb附近，用冲激不变法设计归一化系统函数为：。滤波器的截止频率和增益k对捕获时间和环路的稳定性都有影响，调整这两个参数，使之达到最佳状态。

DTTL符号定时恢复

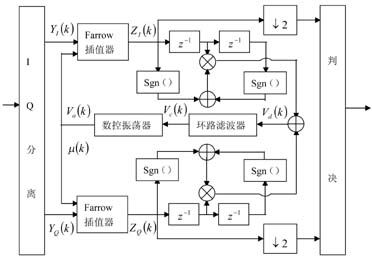
QPSK调制的DTTL符号定时恢复算法原理如图4所示。该算法由Farrow插值器、定时误差检测器、数字环路滤波器及数控振荡器等四部分组成。可以看出，它实际上是一个带锁相环的反馈定时误差同步器。符号定时恢复主要是通过不断调整Farrow插值器的参数，使得输出的样点值抽样在每个符号周期的最大值上。该算法工作在2个样点/符号。

图4中的Farrow插值器使用线性插值公式Z1(k)=(1-μ(k))Y1(k-1)+μ(k)Y1(k)，其中0≤μ(k)<1。调整μ(k)的值，即可使样值采样在最佳时刻。误差检测器可表示如下。



Vd(k)=Z1(k-1)[sgn(Z1(k))-sgn(Z1(k-2))]+ZQ(k-1)[sgn(ZQ(k))-sgn(ZQ(k-2))]

环路滤波器采用二阶数字环路滤波器，其输入输出关系可表示如下。

Vc(k)=Vc(K-1)+KpVd(k)+(Ki-Kp)Vd(k-1)

关于比例增益常量Kp和积分增益常量Ki的选择，可以参考文献4。数控振荡器的控制字Vo按照下式每个符号调整一次。

Vo(k)=Vo(k-1)+KoVc(k)

式中Ko为数控振荡器灵敏度增益常量。最后，分数索引μ(k)可按下式更新。

μ(k)=mod(μ(k-1)+Vo(k-1),1)

式中mod表示取余。

Kalman DFE自适应均衡器

Kalman DFE自适应均衡器的均衡原理如图5所示。


     
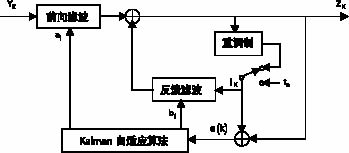
由图5可以看出，DFE均衡器包含两个横向滤波器，一个横向滤波器用于线性的前向滤波处理，其判决结果反馈给另一个横向滤波器。如果前面的判决是正确的，则反馈滤波器就能消除由前面码元所造成的串扰。反馈滤波器的抽头系数由包括前向滤波器所造成的信道冲激响应拖尾所决定。不难理解，只要误码率小于1/2，原则上就能保证收敛。

图中前向滤波器为M阶，反馈滤波器为N阶；tn为训练序列；YK为前向滤波器的输入，ai为其抽头系数；IK为反馈滤波器的输入，bi为其抽头系数；ZK为DFE的输出；e(k)为误差信号。均衡器工作时，总是先由接收到的同步序列或训练序列tn等已知序列进行训练。在训练期间，DFE均衡器将内部产生的理想信号作为反馈输入信号，由LMS或RLS算法对信道进行估计，同时调整前向与反馈滤波器的抽头系数，收敛到均方误差最小。当残差足够小时，均衡器被切换到直接判决模式，即由判决符号重调制生成的参考信号作为反馈输入，均衡器将继续工作在均方误差最小状态。

由图5可知，

令XT(k)=YK,YK+1,...,YK+M-1,IK-1,IK-2,...,IK-N)

WT(k)=(a1,a2, ..., aM,b1,b2, ...,bN)

其中，T表示转置，则误差信号e(k)表示如下。

e(k)=IK-ZK=IK-WT(k-1)X(k)

Kalman算法的精髓在于，已知W(k-1)，递推计算W(k)，其递推步骤如下。

初始化：0<ω<1；W(0)=0；P(0)=I，I表示单位矩阵。

for k=1 to n do ：e(k)=I(k)-XT(k)W(k-1)
K(k)= P(k-1)X*(k)
ω+XT(k)P(k-1)X*(k)
P(k)= [p(k-1)-K(k)XT(k)P(k-1)]
W(k)=W(k-1)+K(k)e(k)

其中，K(k)为卡尔曼增益向量，P(k)为X(k)的协方差矩阵。均衡器系数随时间改变的量等于误差e(k)乘以卡尔曼增益向量K(k)。因为是M+N维的，所以每一个抽头系数实际上受到K(k)的一个元素的控制，从而获得快速收敛。