基于DSP的实时数据无损压缩实现

数据压缩技术能减少传输所用的时间和存储空间，在有限的信道容量内传输更多的有用信息，有助于降低功率和带宽要求，改善通信效率。反之，如果不进行数据压缩，则无论传输或存储都很难实用化[1]。

1 硬件及实现原理

结合本设计的实际情况，由于压缩算法比较复杂，计算量大，在压缩数据时必须采用浮点型运算。另一方面，由于处理精度要求高，所以需要选择浮点型DSP。基于上述考虑，选用TI公司的一款性价比非常高的浮点芯片TMS320C6713。其主频225MHz，每周期执行8条32bit指令，最高定点运算能力为 1800MIPS，浮点运算能力为1350MFLOPS，32位指令集，而且内部自带256KB的RAM，4KB程序缓冲器和4KB的数据缓冲器，可以通过外部存储器接口EMIF(External Memory Inter Faces)扩展SDRAM和Flash[2]。在本设计中，对原始数据按照每2 048B为一组进行压缩。压缩的最小单位是2 048B，且压缩率不固定，对于某组特定数据压缩后可能比原来的数据还要大。压缩前后的数据都需要放到DSP的RAM中进行处理，其256KB的RAM不能满足本设计存储要求，需要通过EMIF扩展存储空间。SDRAM选用Micron公司的MT48LC2M32B2。其数据总线为32位，存储空间为 64Mbit。工作电压为3.3V，内部流水线结构保证了芯片的高速运行。SDRAM可以与EMIF无缝接口。EMIF的CE0连入片选引脚CS，将 SDRAM映射到CE0地址空间（0x80000000－0x80800000）。Flash是系统在断电后用来保存程序和初始化数据的存储器，系统上电时，由引导程序将DSP的应用程序从该存储器引导到系统的高速存储器RAM中。本设计用AMD公司生产的1M×8bit/512K×16bit AM29LV800-70 Flash存储器，其数据宽度为8位、16位可选，采用3.3V供电，访问时间仅70ns。EMIF的CE1连入片选引脚CE，将Flash映射到CE1 地址空间地址范围为0x90000000～0x90100000，寻址空间为1MB[3]。

通常在高速数据采集系统中，数据处理速度及数据传输速度与前端A/D转换器的采集速度不一致。为了协调它们之间工作，可以加入数据存储器或者数据缓存器（FIFO）进行数据缓冲，使得前端数据采集和后级数据处理能够协调工作。在本设计中，前端的采样速度为27Kb/s；且数据流是连续的。DSP的主频为 225MHz，经过锁向环分频后其读取数据的速度为38Mb/s左右。DSP若一直等待读数据，会大大降低其数据的处理能力。DSP读入数据后，马上对数据进行压缩，压缩后把相应的数据写到输出FIFO。同理，发送模块的处理速度为18Kb/s。DSP写输出FIFO的速度也在38Mb/s左右。显然，前端与DSP及DSP与发送模块的处理速度不是一个数量级。所以在前端与DSP之间，DSP与发送模块间分别加了两个FIFO。本设计中FIFO1、 FIFO2均选用IDT72V19160，其存储空间为128KB，16位并行数据总线，可达到100MHz的操作时钟。原理框图如图1所示。



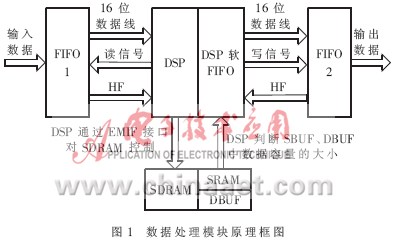
前端通过16位数据总线将数据写入到输入FIFO1中。在程序中通过控制其半满（HF）信号，即当数据超过32KB时（32768+1）， HF信号低电平有效，就会触发一次中断通知可编程逻辑和DSP，DSP进入中断后把2KB的数据从输入FIFO1中读入到SBUF所指向的SDRAM空间中，在进行高速压缩以后，被压缩的数据放到DBUF中。SBUF的数据要与DBUF的数据进行比较，若DBUF中存储数据的容量小于SBUF中的存储数据的容量，就把DBUF中相应的数据写到DSP的软FIFO中，否则，就把SBUF中相应的数据写到DSP的软FIFO中。最终，DSP把压缩后的数据通过其软FIFO写入到输出FIFO2中，等待发送模块把数据读走。

在上述过程中，如果DSP没有等待到中断信号，则返回继续等待，直到检测到中断信号，才读取FIFO1中的数据。在DSP对SBUF中的数据帧压缩的同时，前端以固定的采样率对模拟信号进行采样，并写入到输入FIFO1中。同时DSP把压缩后的数据按每次小于2KB左右的速度写入到输出FIFO2。当输出FIFO2半满，发送模块控制器会把其HF信号通过GPIO口指向DSP。本设计中用GP10实现相应的操作。DSP的GPIO口可以设为输入引脚，在中断向量表中定义后，其本身可以当作中断使用。这样DSP可以把采集到的实时数据源源不断地写入到FIFO2。整个信号处理模块的不同子模块都处于并行工作状态，较好地实现了数据的实时压缩，提高了压缩效率。

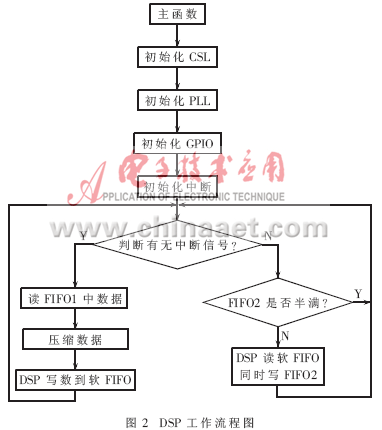
设备上电DSP复位后，由其内部固化的自引导程序(BOOT)将存于Flash存储器的程序和数据搬移至内部 RAM中，然后DSP即可以开始读取压缩算法的应用程序，继续运行。DSP的工作流程图如图2所示。上电以后，首先初始化DSP的CSL函数库，然后初始化PLL、GPIO及关中断寄存器，等待中断信号的来临。




2 算法的选择

无损压缩就是对信源信息进行压缩编码后在解压缩时能够完全恢复，也即在压缩和解压缩过程中对信源信息没有丝毫损失。常用的无损压缩方法有Shannon- Fano编码、Huffman编码、游程(Run-length)编码、LZW(Lempel-Ziv-Welch)编码和算术编码(ARC)等。对许多信息而言，没必要完全保留全部特征。在允许一定精度损失的情况下，可以获得更高的压缩编码效率。这类压缩编码方法成为有损压缩。本设计采用无损压缩，不再讨论有损压缩。

无损数据压缩算法可以分为统计方法和词典编码方法。统计方法当以Huffman编码和算术编码(ARC)为代表。这种方法需要统计信源符号的概率分布情况，并根据统计结果产生压缩码。算术编码是一种高效清除字串冗余的算法。仙侬信息论把字符aj出现的自信息量定义为I(aj)=-logpj I(aj)亦称自信息函数，其含义实际是随机变量X取值为aj时所携带信息的度量。自信息量的概率平均值，即随机变量I(aj) 的数学期望值，称做信息熵或简称熵。算术编码从全序列出发，采用递推形式连续编码。它不是将单个的信源符号映射成一个码字，而是将整个输入符号序列映射为实数轴上[0，1)区间内的一个小区间，其长度等于该序列的概率，再在该小区间内选择一个有代表性的二进制小数，而且是一个介于0和1之间的二进制小数作为实际的编码输出，从而达到了高效编码的目的。例如算术编码对某条信息的输出为1010001111，它表示小数0.1010001111，也即十进制数 0.64。不论是否为二元信源，也不论数据的概率分布如何，其平均码长均能逼近信源的熵。算术编码的过程实际上也就是信源编码试图将任意的信息流与0、1 之间的间隔建立一一对应关系的过程。这样要表示的信息流越长，则表示它的间隔就越小，用于表示这一间隔所需的二进制位就越多。

算术编码在编码前要求预先统计各信源符号概率，但无须排序，只要编、解码端使用相同的符号顺序即可。建立合理的信源概率模型是进行算术编码的关键。信源概率模型的建立方法一般有两种：一种是自适应的模型，是在不断输入信源的过程中对信源符号出现的概率进行统计，模型是在编码过程中逐步建立起来并不断更新；另一种是事先统计的模型，是在编码前就对所有输入信源符号的出现频率进行事先统计，而编码过程中模型不再改变。基于两种模型算法的不同之处：事先统计模型在编码之前就己经建立，编码过程中不再更新，故压缩效率与输入字节数关系不大；而自适应模型是在编码过程中建立并不断更新，当输入信源的数据量较大时，出现概率大的字符编码位数较少的优越性才能得以体现。在复杂度上，由于后者需要不断对模型进行更新，故运算量较大。

词典编码方法则是基于数据中许多结构频繁重复再现这一事实，人们可以对相同符号串分配同一码字、通过索引或者其他诸如此类的方法编码。LZW算法可以在对数据统计特性一无所知的前提下，使压缩率接近己知统计特性时所能够达到的压缩率，其运算速度快。LZW算法压缩的原理在于用字典中词条的编码代替被压缩数据中的字符串。字典中的词条越长越多，压缩率就越高。所以加大字典的容量可以提高压缩率。但从字典中查找词条是算法中最费时的工作，其字典的容量受到计算机内存限制，且字典也存在被填满的可能。当字典不能再加入新词条后，过老的字典就不能保证高的压缩率。

不同的压缩算法有不同的优点和缺点，不同算法的复杂性对空间的要求及压缩率也不同。压缩算法不仅仅依赖于压缩方法本身，也依赖于被压缩文本的特点。在本文中，由于是对实时数据的压缩，对压缩过程的时间性能要求高，所以采用事先统计模型的ARC。实验证明，采用事先统计模型的ARC，其运算速度与LZW算法速度相近。而ARC算法在压缩速度和压缩去除率上都优于LZW算法。