基于比时法的晶振频率测量建模与分析

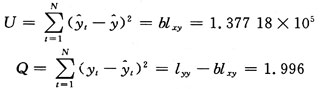
式中：U称为回归平方和，它反映了在y的总变差中由于x和y的线性关系而引起的y变化的部分；Q称为残余平方和，即所有测量点距回归直线的残余误差平方和。

若总的平方和由N项组成，其自由度就为N-1，总的离差平方和的自由度可分为回归平方和的自由度υU和残余平方和的自由度υQ之和，即：

在一元线性回归中，υU=1，υS=N-1，则Q的自由度υQ=N-2。由回归平方和与残余平方和的意义可知，一个回归方程是否显著，也就是y与x的线性关系是否密切，取决于U及Q的大小，U愈大Q愈小，说明y与x的线性关系愈密切。通常可以采用F检验法来对方程进行显著性检验。对于一元线性回归，将U及Q的值代入上式得到统计量F：

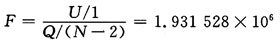
由F分布表可以查出，F≥F0.01(1，28)=7.64。可认为回归是高度显著的。

残余平方和Q除以它的自由度υQ所得商：

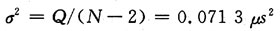
称为残余方差，它可以看作排除了x对y的线性影响后，衡量y随机波动大小的一个估计量。残余方差的平方根：

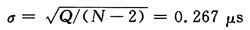
称为残余标准差，它可用来衡量所有随机因素对y一次性测量平均变差的大小，σ愈小，则回归直线的精度愈高。

把平方和及自由度进行分解的方差分析数据结果归纳在一个表格中，如表3所示。

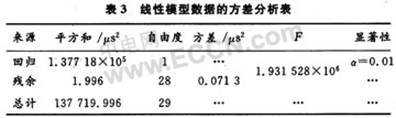
从表3可以看出，在30 s时间内，晶振实际频率与其标称频率的相对偏差引起的误差平方和为1.377 18×105μs2，其他各种随机因素引起的误差的平方和为1.996μs2。晶振相对频偏引起的误差远远大于其他因素引起的误差，表明了晶振频率误差贡献主要来源于实际频率与标称频率之间的频偏。通过频率修正即可得到一种高稳定度的频标源。

5 结语

以上分析结果表明，该晶振频率误差主要来源于实际频率与标称频率的相对偏差，随机误差对晶振整体误差的贡献很小。通过对晶振标称频率值进行在线补偿可以消除其相对频偏，从而获得一种具有较高稳定度的频率源，可为需要时间显示的场所提供高精度的时间服务。