实现放大器与ADC之间的共模融合

        当我们拼命折腾自己，藐视摩尔定律，不断实现更小的几何尺寸和IC工艺时，供电或偏置轨也要走这条路了。大部分器件都用单边电源给元件供电，但我们可以看到大部分信号仍是双极性形式。为了给放大器和转换器建立新“零”点或中心码，需要在两者之间定义一个共模(CM)电压。否则，您的设计基本上无法工作。
两个器件之间的公共地有时比较隐蔽。对于放大器和模数转换器(ADC)，在指定新型信号链应用时经常会忽视这些需求，这一般是因为数据手册被忽略太久了！两个器件当然都会有些限制规定，以便适应输入/输出范围和电源。所以要小心谨慎，不管怎么样，都应读一下数据手册。
共模定义
现在，您已经选好了放大器和高速ADC，还会有什么不妥吗？您已经进行了大量的噪声分析，并找到了符合当前应用技术规格的设计。您是否考虑过两个相连器件之间的CM电压规格？问倒您了吧！
客户在不了解规定两个器件处理性能的这一参数时，就会向技术支持人员提出疑问。如果采用交流耦合设计，并且不需要任何直流内容，您读到这里就可以了。否则，对于交流耦合应用，需在放大器/转换器之间使用一个耦合电容来打破这种CM不匹配。这样，设计才能够优化放大器输出和转换器输入的CM偏置。
如果属于直流耦合应用，就需要保留信号的直流内容。CM在这里非常重要，它能使信号精确分解成数字位、代码和最低有效位(LSB)。
CM电压只是信号移动（图1）的中点。如果您是一个转换器迷，您还可以将它看作是新中点或零代码。作为放大器，通常通过一个VOCM引脚或某种类似的器件，在输出端建立CM。不过要小心，这些引脚也有特定的电流和电压范围要求。



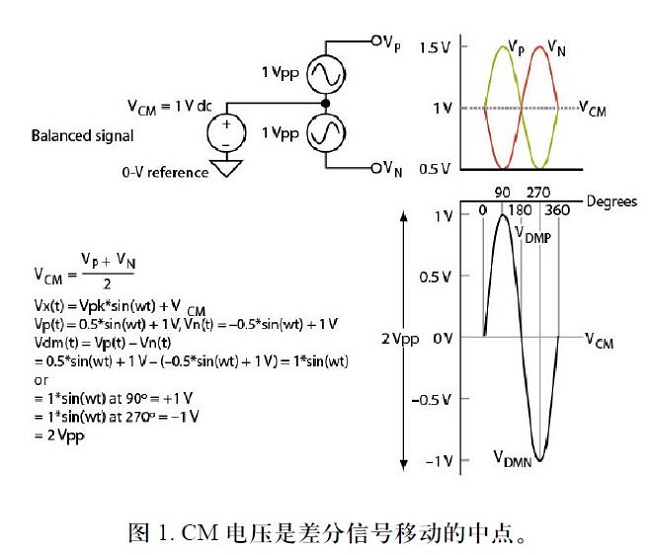
最好是查阅放大器数据手册，并且/或者使用不会使电路内部的任何相邻电路或基准点负荷过重的稳定偏置点。不要只是提取一个转换器的基准电压引脚(VREF)，它通常是转换器满量程的一半，可能无法提供充分的高精度偏置。
谨慎起见，也应查阅转换器数据手册上的引脚技术规格。一般而言，电阻容差1%的简单分压器和/或缓冲器驱动器之类，不能正确设置放大器的CM偏置。


       
转换器一侧需要在模拟输入端具有确定的CM偏置，以便将此基准电压建立于地之上。但在我们继续插拔之前，看看自己是否用的是缓冲或无缓冲转换器。如果是无缓冲转换器（又称开关电容型），则需要在模拟输入端提供一个外部CM偏置。
缓冲转换器一般通过转换器的内部缓冲进行设置，具有自偏置模拟输入。此电平一般是电源电压的一半加上（AVDD/2+0.7V）之上的二极管压降，而无缓冲转换器没有内部缓冲和自偏置，需要AVDD/2或模拟电源电压一半的CM偏置。因此，设计人员必须从外部提供此CM偏置，这可通过各种方式进行。
部分转换器具有一个VCM或CML引脚，它允许设计人员通过多个与模拟输入相连的端接电阻来提供偏置。设计人员还可以使用一个变压器的中心抽头，或仅在模拟输入的每个端脚上提供多个电阻分压器，将其连在AVDD和地之间。
同样，要远离VREF引脚或查看数据手册。大部分具有此类标注的引脚并不用于供应CM偏置，除非通过一个放大器从外部对其进行缓冲。请记住，VREF引脚在转换器内设置所有内部基准电压偏置。这也是转换器输入满量程的一个功能。
如果VREF引脚使用不当（即，负荷过重），实际上可能无意间偏移转换器的输入满量程范围。因此，可能会限制系统的总动态范围。或者，更糟的是，降低转换器的性能。图2为一些正确的电路示例。



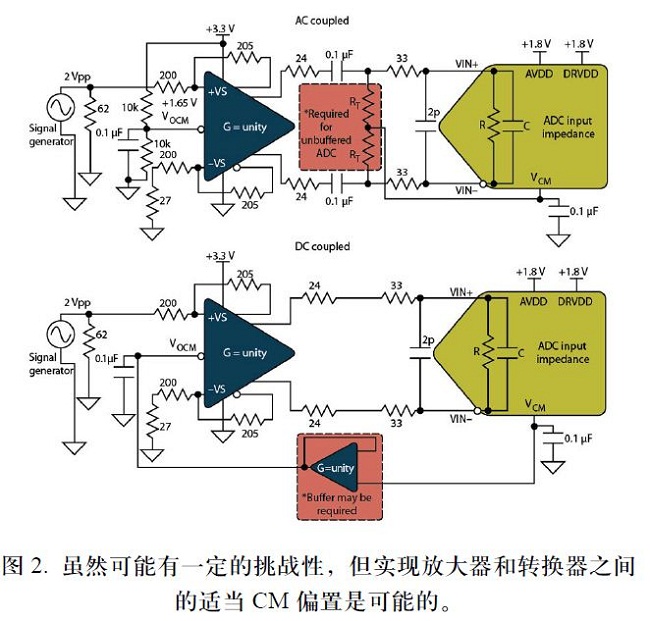
打破共模
如果未提供或保持CM偏置，转换器将产生增益和失调误差，使获取的总体测量性能下降。您的转换器输出将如图3所示或有某些变动。输出频谱将与一个过载满量程输入非常相似。这意味着转换器的“零”点偏离中心，没达到最优。



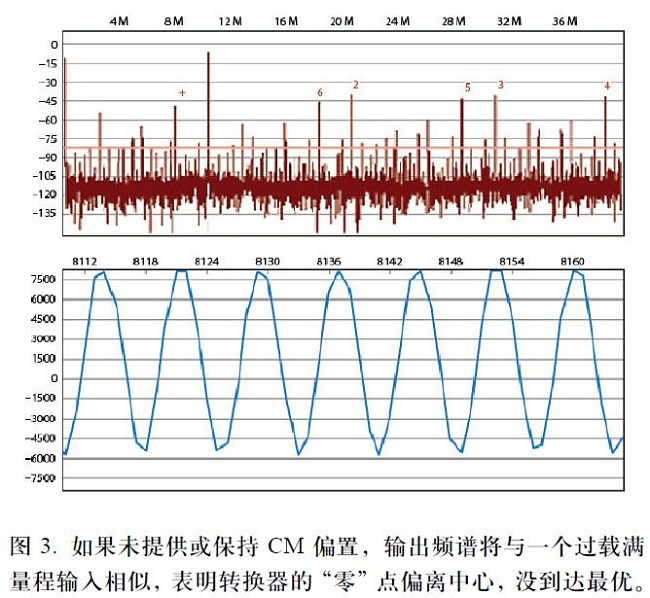
设计人员可能会发现转换器会较早“削波”或者达不到满量程。近年来，由于转换器开始使用1.8V电源，这一问题变得更为严重。这意味着模拟输入的CM偏置为0.9V或AVDD/2。并非所有的单电源放大器都能支持如此低的CM电压，同时还能保持相对较好的性能。
但是，许多新型放大器已经适应此类电压，并在市场上出售。因此，需查看哪些放大器可以用于您的新设计。并不是任何旧款放大器都能使用，因为裕量可能非常有限，并且内部晶体管可能开始老化。
如果将双电源与放大器配合使用，大多数情况下应该会有充足的裕量来实现适当的CM偏置。缺点是增加了一个额外的电源，这意味着设计中需要更多的器件、更高的成本以及更大的功耗。简单的反相器电路有助于解决这一问题，但设计人员及其管理者需要就折衷方案达成一致。