了解高速ADC的交流特性

        在消费、医疗、汽车甚至工业领域，越来越多的电子产品利用高速信号技术来进行数据和语音通信、音频和成像应用。尽管这些应用类别处理的信号具有不同带宽，且相应使用不同的转换器架构，但比较候选ADC（模数转换器）及评估具体实施性能时，这些应用具有某些共同特性。具体而言，从事这些不同应用类别的设计师需要考虑许多常见的转换器交流性能特征，这些特征可能决定系统的性能限制。
量化
所有ADC 接收在时间和幅度上连续的输入信号，并输出量化的离散时间样本。ADC 的双重功能（量化和采样）提供从模拟到数字信号域的有效转换，但每种功能对转换器交流性能均有影响。
由于数字转换器用于分析连续输入信号的代码数量有限，其输出会在锯齿波形上产生误差函数。锯齿边沿对应于ADC 的码字跃迁。
为了测量量化误差的最佳情况下的噪声作用，假设将满量程正弦波输入完美数字转换器：



其中q 是LSB 的大小，N 是位数。该波形的均方根幅度即为幅度除以2 的平方根。



均方根量化噪声为



均方根满量程信号与均方根量化噪声之比为ADC 提供了理想SNR，可用分贝表示：


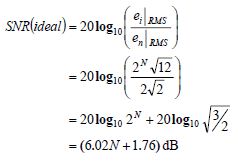
（公式1）
请记住，该公式给出的是N 位转换器的理论限制。真实量化器无法达到这一性能水平，同时真实转换器还有其他噪声源，但这一数字可以作为判断候选ADC 的参考。
采样
在采样器特性中，最为人熟悉的是在大于采样速率一半的频率(fs/2)下混叠信号能量的特性。这一半采样速率限制称为奈奎斯特频率，用于将频谱分割为大小相等的区段，即奈奎斯特区。第一奈奎斯特区范围从DC 至fs/2。第二奈奎斯特区占据fs/2 至fs 之间的频谱，依此类推。
现实中，采样器混叠所有奈奎斯特区上的信号。例如，频率fa下的基带信号镜像呈现为fs ± fa、2fs ± fa，依此类推（图1a）。同样，出现在采样频率附近的信号将向下混叠至第一奈奎斯特区。该信号的镜像也将出现在第三及第四奈奎斯特区内（图1b）。因此输入信号能量不在所需奈奎斯特区内的采样器在混叠作用下将产生该信号在所需奎斯特区内的镜像。
显示为fa（图1b）的带外信号能量不一定来自预期信号源。相反，该能量可能源自噪声源、带外干扰源或采用预期输入信号工作的电路元件产生的失真积。当为您的应用决定必要的失真性能时，这是一项重要的考虑因素。


a的镜像）与采样频率fs 及其谐波(A)出现偏移。频谱偏移等于±fa。出现在采样速率附近的信号、噪声和干扰频谱向下混叠至基带(B)内。镜像也将出现在较高奈奎斯特区内。">
图1：采样器导致基带信号fa的镜像）与采样频率fs 及其谐波(A)出现偏移。频谱偏移等于±fa。出现在采样速率附近的信号、噪声和干扰频谱向下混叠至基带(B)内。镜像也将出现在较高奈奎斯特区内。

通过在信号链内采样器输入之前加入基带抗混叠滤波器，可以减小采样器可用的带外信号能量。虽然理论上可以仅在需要数字化的最高频率到达两倍时采样，模拟域内不存在所谓的砖墙式滤波器，即零过渡带的滤波器。过采样，即在大于2fs 的频率下采样，为抗混叠滤波器过渡带提供一些频谱空间。
如果ADC 量化噪声与交流输入信号无关，则噪声分布于第一奈奎斯特区中。在这种情况下，过采样还会通过加宽奈奎斯特区减少有效量化噪声，从而在采样速率每次加倍时将SNR（信噪比）增加3 dB。这相当于具有固定通带的抗混叠滤波器。如果进行充分过采样，抗混叠滤波器可削弱带外信号成分，使其混叠镜像保持在本底噪声以下。
应注意，如果输入信号锁定在采样频率的整数约数处，量化噪声将不再表现为奈奎斯特区中的均匀能量分布。这种情况下，量化噪声将表现为关于信号谐波的群集。为此，在选择采样速率时，应仔细考虑应用信号的频谱特性。


       
SINAD 和ENOB
如果失真积和带外频谱成分混叠无法保持在本底噪声以下，则会形成SINAD（信号-噪声和失真比）。转换器在输入信号额定条件下将以dB 表示SINAD。转换器ENOB（有效位数）可能是ADC 最常提到的交流规格，它便是以位而非dB表示的SINAD：


（公式2）
如果失真积和混叠信号能量保持在本底噪声以下，则SINAD= SNR。在此情况下，公式2 只是公式1 对N 求解的调整形式。更常见的情况是SINAD n(i)是来自起作用源的噪声，作用源处于由m 个不相关源组成的系统内。
起作用噪声源之一来自采样时钟边沿时序的不确定性，产生孔径抖动噪声。可以说，该噪声得出采样器正在针对移动目标捕捉交流信号的事实。采样边沿时序的变化导致采样器捕捉幅度的统计分布，即噪声（图3）。信号频率越高，信号斜率或压摆率越大，因此边沿时序既定变化导致的幅度误差越大。这样，既定孔径抖动量的效果便取决于信号频率。


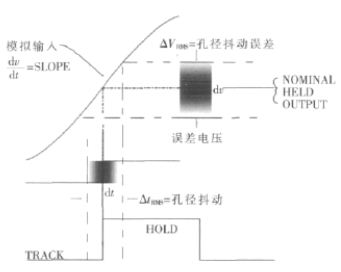
图3：孔径抖动（采样时间上的不确定性）产生噪声幅度，由于抖动时间内的信号压摆，该幅度取决于信号频率。

由孔径抖动引起的SNR 为


（公式3）
其中f 是信号频率，tj 是均方根孔径抖动。通常在挑选ADC时，问题在于目标应用在既定频率信号的SNR 要求下可以容忍的最大幅度抖动。整理公式3 得出


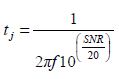
（公式4）
请注意，除了转换器内的抖动源外，您的应用电路内也有抖动源。因此，电路实现的净性能与转换器选择和设计其他方面（通常是时钟产生电路和电路板布局）的品质都有关系。
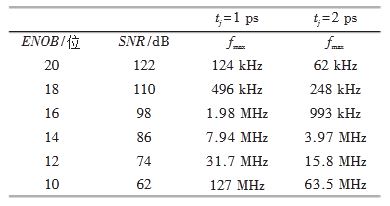
为了解抖动影响既定ENOB 最大信号频率的程度，可分别来看1 ps 和2 ps 抖动噪声远超其他性能限制参数的两个系统。整理公式4，我们可以针对既定抖动计算产生指定ENOB（或SNR）的最大信号频率。
表1. 对比抖动时间相差两倍的系统




       
失真积
信号链内的非线性造成了许多失真积，通常是HD2（第二谐波失真）、HD3（第三谐波失真）、IMD2（二阶交调失真）和IMD3（三阶交调失真）。线性电路内的失真倾向于随信号接近有源元件线性工作范围的极限而逐渐增加。在代码空间突然结束的ADC 内则不是这样。
因此，重要的是输入跨度内有足够的范围容纳您要进行低失真量化的预期输入幅度，特别是在处理复杂宽带信号时。最终，选择标称输入幅度是为了平衡信号跨度余量，避免限制优化SNR 的需要。
顾名思义，谐波失真会产生数倍于信号频率的信号伪像。相比之下，交调失真源自包含两个或两个以上频率信号（事实上是任何复杂波形）的信号处理非线性，从而产生输入频率之和或差。
在窄带应用中，严格调谐的抗混叠滤波器可削弱某些谐波失真积，甚至IMD2 的加性分量（图4）。另一方面，出现在2f2 - f1 和2f1 - f2 的IMD3 减性分量由于可出现在信号频谱内而较为不利。


图4：5 MHz 和6 MHz 双音输入信号说明了HD2（10 MHz 和12 MHz 下）、HD3（15 MHz 和18 MHz 下）、IMD（1 MHz和11 MHz 下）和IMD3（4 MHz 和7 Mhz 下）。其中，IMD3 积由于接近源信号，最难通过抗混叠滤波器削弱。

无杂散动态范围(SFDR)
SFDR（无杂散动态范围）衡量的只是相对于转换器满量程范围(dBFS)或输入信号电平(dBc)的最差频谱伪像。比较ADC时，请务必确定两种基准电平以及工作和信号条件。在数据手册规格间直接进行比较需要基准和信号相匹配（图5）。


图5：转换器制造商可以就转换器满量程(dBFS)或具体输入信号幅度(dBc)规定SFDR 性能。在进行数值对比前，请确保候选转换器是以相似方式进行性能规定的。

虽然SFDR 表现为转换器规格表内的数值，该测量值本身只是采样速率、信号幅度、信号频率和共模工作点的参数。只有考察候选转换器的特性曲线，才能深入了解转换器在近似于目标应用的工作和信号条件下的性能。