运放稳定性连载7：环路稳定性主要技巧与经验（1）

ZI 和 ZF 幅度十倍频程准则

我们从本系列的第2 部分了解到ZI 和ZF 网络。图4.9 详细给出了ZI 输入网络中的幅度 “十倍频程准则”。如果我们标定Rn = RI/10（Rn 在数值上比RI 小“十倍”），则我们可以确定在高频情况下，当Cn 阻抗短路时，Rn将把高频设置为RF/Rn。这样标定使我们能更容易地绘出1/β 曲线中起主要作用的一阶结果。幅度十倍频程准则的另一个优势是它迫使我们加入极点/零点对——fp 与fz，这样在其彼此一个十倍频程以内，以及因此在fp 与fz之间，相移将保持平坦。


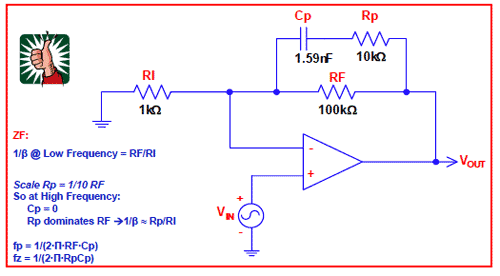
图4.9：ZI 幅度十倍程准则

图字：
ZI：低频处1/β=RF/RI
标定Rn = RI/10
这样在高频处：
Cn=0
Rn 比 RI 占优势 →1/β≈RF/RI
fp=1/(2⋅π ⋅Rn ⋅Cn )
fz=1/(2⋅π ⋅RI ⋅Cn )

图4.10 给出了ZF 反馈网络中的幅度“十倍频程准则”。如果我们标定Rp = RF/10（Rp 在数值上比RF 小“十倍”），则我们可以确定在高频情况下，当Cp 的阻抗短路时，Rp 将把高频设置为Rp/RI。这样标定使我们更容易绘出1/β 图中起主要作用的一阶结果。正如在输入网络ZI 中一样，幅度十倍频程准则的另一个优势是它迫使我们加入一个极点/零点对fp 和fz，这样在其彼此一个十倍频程以内，以及因此在fp 与fz 之间，相移将保持平坦。


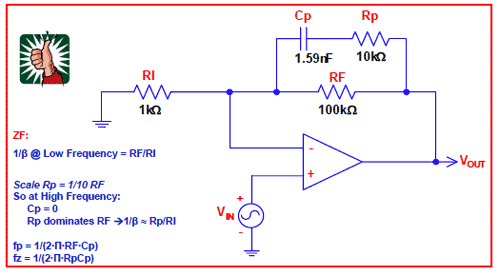
图4.10：ZF 幅度十倍频程准则

图字：
ZF：低频处1/β=RF/RI
标定Rp = 1/10RF
这样在高频处：
Cn=0
Rp 比 RF 占优势 →1/β≈Rp/RI
fp=1/(2⋅π ⋅RF⋅Cp )，fz=1/(2⋅π ⋅Rp⋅Cp )
双反馈路径

随着本系列的不断深入，我们将看到，常常运用反馈电路来确保获得良好的运放稳定性，需要使用一个以上的反馈路径。为更方便地分析和综合此类多级反馈，我们将使用叠加原理。图4.11 定义了叠加原理。在此，我们将先单独分析每个影响，然后再将主要影响作为我们反馈的最终结果。


图4.11：叠加原理

摘自：Smith,Ralph J，“电路、器件与分析”，John Wiley&Sons 公司，1973 年第三版，纽约。

图字：
叠加原理：如果起因和影响线性相关，则同时起作用的几个起因造成的总的影响就等同于单个起因每次单独作用的影响之和。

在图4.12 中，我们看到一个使用了两条反馈路径的运放电路。第一条反馈路径FB#1，位于运放的外部，经过Riso和CL后返回，并经过RF和RI回到运放的输入端。第二条反馈路径FB#2，位于运放的外部，经过CF然后返到运放的输入端。这里分别绘制了与这些反馈等效的1/β曲线。此推导的详细过程将在本系列的后续部分给出。当围绕运放使用一个以上反馈路径时，为运放提供最大反馈电压的反馈路径就成为主要的反馈路径。这意味着如果为每个反馈都绘制了1/β图，则在给定频率处，1/β最小的反馈就将在该点起主要作用。请记住，最小的1/β即最大的β，而由于β=VFB/VOUT，因此最大的β即表明反馈到运放输入端的电压最大。请记住一个简单的类比，即：如果两个人对着你的同一只耳朵讲话，那么哪个你听得更清楚一些呢——当然是讲话声较大的那个！所以运放将会“听”具有最大β或最小1/β的反馈路径。在FB#1 或 FB#2 的任何频率上，运放所看到的的净1/β曲线应该是较低的那个。


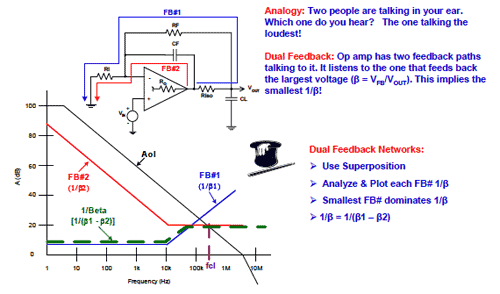
图4.12：双反馈网络

图字：
类比：两个人同时对着你的耳朵讲话。你更能听见哪个呢？当然是讲话声大的那个！

双反馈：有两条反馈路径在对运放“讲话”，它主要倾听反馈电压较大的路径 (β = VFB/VOUT)，这意味着最小的1/β值！

双反馈网络：
- 采用叠加原理
- 分析每个FB#1/β 并绘图、
- 最小FB# 决定了1/β
- 1/β=1/(β1-β2)。

当围绕一个运放使用双反馈路径时，有一个极其重要的情况必须避免，即“BIG NOT”。如图4.13 所示，其中的运放电路导致反馈路径中产生BIG NOT 现象，该现象在1/β 曲线中可看到，图中1/β 斜率从+20db/decade 突然变成了-20dB/decade。这种改变意味着，在1/β 曲线上有中一个复共轭极点，这样相应地在环路增益曲线上即有一个复共轭零点。复零点与极点在其对应的频率上引起一个 +/-90 度的相移。此外，复零点/复极点的相位斜率，在其出现频率位置附近的一个狭窄频带内可从+/-90 度变化至+/-180 度。复零点/复极点的产生在闭环运放响应中可能会引起严重的增益尖峰，这是很不希望看到的情况，尤其在功率运放电路中。


图4.13：双反馈与BIG NOT

图字：警告：这对你的电路可能很危险！

双反馈和BIG NOT：
1/β 斜率从+20db/decade 变成-20dB/decade
- 表明在1/β 曲线上有一个“复共轭极点”
- 表明在Aolβ（环路增益）曲线上有一个“复共轭零点”
- 在复零点/复极点的频率处有+/-90 度的相移
- 在复零点/复极点所出现频率位置附近的一个狭窄频带内，相位频率可以从+/-90°/decade 变化至+/-180°，这取决于不同的阻尼系数
- 复零点/复极点在闭环响应中可能会引起严重的增益尖峰

图4.14 给出了不同阻尼系数情况下复共轭极点的幅度图。不论阻尼系数如何，极点都表现为双极点且斜率为-40dB/decade。但相位将给出不同的情况。


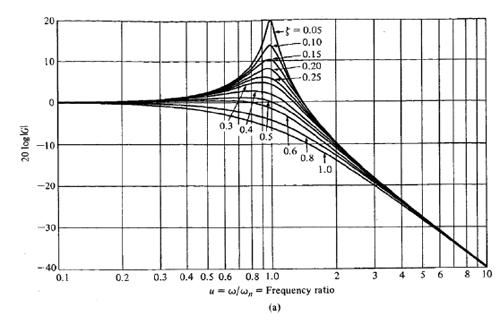
图 4.14：复共轭极点幅度举例

摘自：Dorf, Richard C.，“现代控制系统”，Addison-Wesley 出版公司，麻省雷丁，第三版，1981年。

图4.15 给出了复共轭极点的相位图。很明显，由于阻尼系数不同，故相移相对于单纯双极点而言可能会有极大的不同。在双极点情况下，我们预计在该频率处的相移为 -90 度，斜率为-90 degree/decade（阻尼系数 =1）。


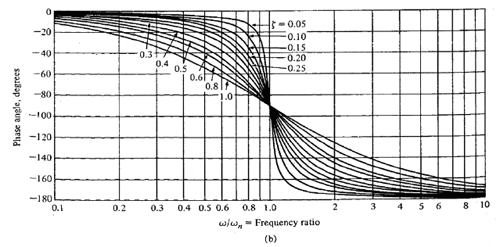
图4.15：复共轭极点相位举例

摘自：Dorf, Richard C.，“现代控制系统”，Addison-Wesley 出版公司，麻省雷丁，第三版，1981年。