计算电磁学在电磁兼容仿真中的应用

随着电子技术的发展，电子、电气设备越来越广泛地应用于航空飞行器上，恶劣的电磁环境往往使电子或电气设备不能正常工作，导致航空通信、控制系统性能的降低。因此，电磁兼容性就成为工程设计中的一个重要课题。只有在整个系统的初期设计时，对系统的电磁兼容性进行预测，对不满足电磁兼容要求的部分进行优化处理，才能最终实现整个系统的高可靠性。

　　近年来，计算电磁学发展迅速，理论日趋成熟和完善，并广泛应用在电磁兼容领域。利用计算电磁学理论解决工程中电磁兼容问题，不仅提高了计算的准确性，而且降低了成本，为在研发初期掌握产品可能出现的电磁兼容问题提供了有效的手段和途径。因此，仿真计算对于那些利用实验和测试方法难以解决的电磁兼容问题是一种很好的解决方法。

　　本文介绍了几种常用的数值算法，并对各种算法进行了分析。针对航空用电设备常见的电磁兼容问题，利用计算电磁学理论进行分析和数值仿真，实现了对用电设备电磁兼容性有效的预测，为系统的初期电磁兼容性设计提供了理论依据。

　　1 电磁场数值方法的介绍和比较

　　计算电磁学是现代电磁场理论、现代数学方法和现代计算机技术相结合而产生的一门新兴交叉学科。其主要任务是通过大型计算解决各相关领域中提出的各种极复杂的电磁场问题。

　　当前电磁学中使用较多的数值方法主要有两类，一类是以电磁场问题的微分方程为基础的数值方法，如有限元法(FEM)、时域有限差分法(FDTD)等;另一类是以电磁场问题的积分方程为基础的数值方法，如矩量法(MOM)、多层快速多极子法(MLFMM)等。

　　1.1 有限元法

　　有限元方法是近似求解数理边值问题的一种数值技术，最早于20世纪40年代提出，在六七十年代被引进到电磁场问题的求解中。该方法的原理是用许多子域来代表整个连续区域，在子域中未知函数用带有未知系数的简单插值函数来表示，利用里兹变分法或伽略金方法得到一组代数方程，最后通过求解这组方程得到原边值问题的近似解。原边值问题可表示为：

　　有限元法可以方便地分析具有复杂几何结构和非均匀介质材料的电磁问题，因此，这种方法在各种复杂的静态场问题、导波问题、电磁辐射和散射问题中得到了广泛的应用。

1.2 矩量法

　　自从20世纪60年代Harrington提出矩量法基本概念以来，它在理论上日臻完善，并广泛用于工程之中，特别是在电磁兼容领域，矩量法更显示出 其独特的优越性。它的思想是将待求的积分或微分问题转化为一个矩阵方程问题，借助于计算机，求得其数解。很多电磁场问题都归结为这样一个算子方程：

　　式中：L为算子;g为已知激励函数;f为未知响应函数。展开未知函数f为有限个线性无关的已知简单函数fn之和：

　　式中：an是展开系数;f1，f2，…，fn为展开函数或基函数。将式(8)代入式(7)，再应用算子L的线性，可以得到：

　　选一组线性无关的函数ωm(m=1，2，…，N)，分别与式(9)两边作内积。

　　因为m=1，2，…，N，所以得到N个方程，解出f。

　　矩量法就是这样一种将算子方程转化为矩阵方程的一种离散方法。

　　矩量法更适合于求解具有表面电流分布的各种几何体，如计算天线远、近场辐射场强、方向图等。它的算法简单，不需要设置边界条件，而且对于适当的尺寸，求解速度较快。

　　1.3 时域有限差分法

　　K.S.Yee于1966年提出求解电磁问题的时域有限差分法，其原理非常简单，即直接将时域Maxwell方程组的两个旋度方程中关于空间变量和时间变量的偏导数用差商近似，从而转换为离散网络节点上的时域有限差分方程。

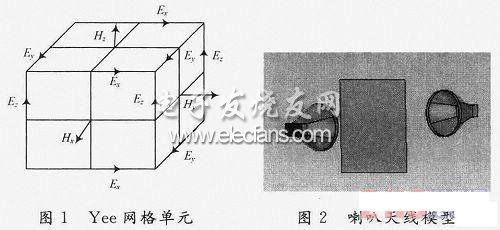
　　为了建立差分方程，首先要将求解空间离散化。通常是以一定形式的网格来划分求解空间，Yee提出了如图1所示的差分网格单元，其特点是在同一网格中，E和H的各分量在空间取值点交叉放置，使每个坐标面上的的四周由分量环绕，同时每个场四周由场环绕。这样，配置符合Maxwell方程的基本要求，也符合电磁波空间的传播规律，使电磁波的时域特性被直接反映出来，直接给出非常丰富的电磁场问题的时域信息。

　　时域有限差分法在天线辐射特性计算、微波电路分析、散射体雷达散射截面等方面有广泛的应用，对于计算孔缝对屏蔽效能的影响具有优越性。

　　1.4 几种方法的比较

　　矩量法既要面对繁难的积分方程，又要注意基函数的恰当选取;既要耐心处理奇异点，又要巧妙构思快速求解技术。相对而言，实施有限元要容易些，只需要注意基函数选取及稀疏矩阵存储方式即可。至于时域有限差分就更容易了。因此一般说来矩量法实施最难，有限元次之，时域有限差分法最易。

就通用性而论，有限元与时域有限差分相近，都很通用，矩量法则稍差。