一种毫米波测速雷达系统的工作原理

将t1，t2，…，tm时刻测得的速度v1，v2，…，vm表示为vi=v0+αTI+βt2 i+εi，i=1， 2，…，m，式中，εi是随机测量误差 ［2］ ，它是一个随机变量，v0、α、β是待定参量，而v0正是要求的初速。根据最小二乘法，求出一组参数^v0、^α、^β，使速度测量值的残差平方和Q= ∑ mi=1 ［vi -（^v0+^αTI+^βt2i）］2 为最校为此推导如下：

由5Q/5v0=0，5Q/5α=0，5Q/5β=0，可得：

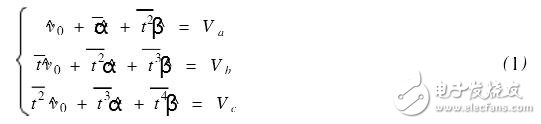
式中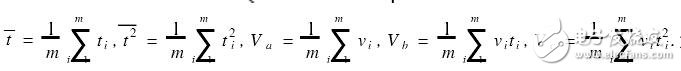，。将（1）式写成矩阵形式则为：

S^θ=B

式中，。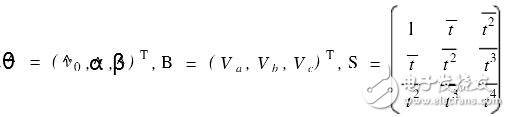

解方程（2），得：^θ=S -1 B。

当随机变量qi相互独立，且服从正态的N（0，σ2 ）分布时，最小二乘估计^θ将有如下优 良统计特性，即（1）^θ是θ的无偏估计;（2）^θ是θ的最小方差估计;（3）VAR（^θ）=（σ2/m）S-1.无偏性说明多次估计的统计平均接近真值。最小方差是指在各种估计中，这种 估计可以使方差达到最小，方差小意味着估计值偏离真值的程度小。因此，VAR（^θ）的大小 可以作为^θ好坏的标准。设C=S-1/m相应的^v0的偏差E（^v0-E^v0）=C11σ2 ，其中C11是矩阵C中对应的元素。为了分析计算方便，设测点间隔为等距，即t2-t1=t3-t2=… =tm-tm-1=Tz，而t1=αpTz=Ty，则矩阵S中的元素成为???? t=Z1Tz，t2 =Z2T2 z，t3 =Z3T3z，t4=Z4T4z.其中，Z1=αp+（m-1）/2，Z2=α2p+αp（m-1）+（m-1）（2m-1）/6，Z3=α3p+3α2p（m-1）/2+αp（m-1）（2m-1）/2+m（m-1）2/4，Z4=α4p+2α3p（m-1）+α2p（m-1）（2m-1）+αpm（m-1）2+（m-1）（2m-1）（3m2-3m-1）/30.根据 线性代数中矩阵求逆的方法可得：

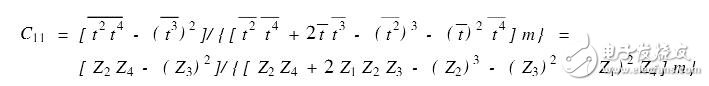
可见估计值^v0的方差E（^v0-E^v0）=C11σ2 与αp及m有关，不同的αp和m有不同的方差。方差越小越好，通常是与测量数据的误差εi的方差进行比较，因此定义η0=E［^ v0-E^v0］2/σ2 =C11为初速v0的方差压缩系数。当η0>1时，说明外推初速的误差大于测量误差;当η0=1时，说明外推初速的误差与测量误差相等;当η0<1时，说明外推初速的误差平均小于测量误差。由前面关系可知η0=C11只与外推步长αp和测量点数m有关，这样可通过选择αp和m来达到所要求的外推精度。表1给出了使η0≈1时，不同步长αp所对应的测点数m，由表可见，外推步长αp越大，则所需测点数越多。毫米波测速雷达通常取m=32.此时要使η0≤1，则可使αp≤6.例如，当测点间隔约为5ms时，则延迟时间要小于30ms才能保证外推初速的精度与测点精度相当。

如果令m=32，则可根据前述公式计算出外推步长αp与外推v0的方差压缩系数η0的关系，如表2所示。

可见，从提高外推精度的观点出发，希望αp取得小一些（m已定），即延迟时间t1取得短一些，但t1也不可取得过短，否则无法避开膛口火焰、冲击振动的影响。根据实际测试需要，测速雷达可以安装在火炮的摇架上，雷达的观测方向与弹丸飞行方向一致，不存在角度修正。若架设在三角架上，此时雷达的观测方向与弹丸飞行方向有一定夹角γ，雷达所测速度，只是弹丸速度在γ方向的分速度，如图2所示。为减小这一测速误差，应尽量减小D，增大 L（即增大延迟时间t1）。

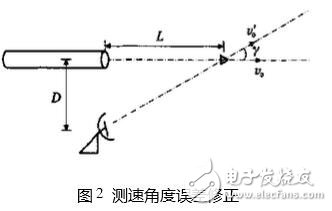
毫米波测速雷达为减小这一测速误差，一般取D=0.2～0.5m，L≥25D，此时有L ≈v0t1，v′0=v0/cosγ，γ=arctan（D/L），测速的相对误差σ=（v0-v′0）/v0=1-v′0/v0= 1-v0cosγ/v0=1-cosγ。例如，测试某式7.62mm步枪，可取D=0.2m，设初速v0=760m/s，则要求t1≥L/v0≥25&TImes;0.2/760=6158ms.取t1=7ms，此时测速精度为σ=1-cos［arctan（D/L）］=1-cos{arctan［012/（760&TImes;7×10-3）］}=711×10-4。

3 结束语

毫米波测速雷达现已成功应用于国内多家靶场，其测试精度达0.1%.经与国外582雷达及丹麦的伟伯尔雷达进行比对试验，测试结果一致。 在实际应用中，发现数据采集的延迟时间参数（外推步长）对测试的初速值精度的影响与理论分析一致，但外推步长的设定也与其它很多因数有关，如它随不同的弹种、环境温度等而变化。对于延迟时间选定的机理和有关理论还需进一步研究或通过大量实验论证，以进一步提高测试精度。

参考