IIR滤波器零相位数字滤波实现及应用

信号（采样点数1024，采样频率4KHz）。从信号的波形可以看出，它具有一定的周期性，主要是以发动机周期性排气产生的噪声为主。

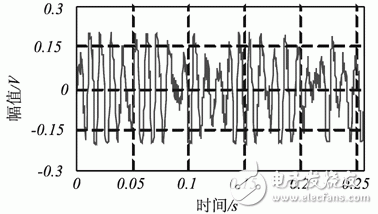
　　图2某型坦克发动机噪声信号

　　采用窗函数（Hanning窗）法设计出某200阶FIR低通滤波器，截止频率为200Hz，分析频率为2KHz，其幅频曲线及相频曲线如图3所示。

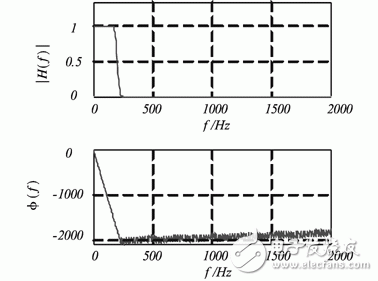
　　图3低通滤波器的幅频特性和相频特性

　　利用该FIR低通数字滤波器对图2所示发动机噪声信号进行差分滤波，滤波后的波形如图4所示

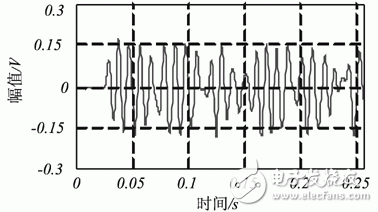
　　图4差分滤波后的发动机噪声信号

　　对比图3和图4所示波形可以看出，差分滤波后，信号变得"光滑"了许多，原来的"毛刺"被滤掉了。但同时也可以看出差分滤波方法存在两个问题：一是滤波后的信号相对与原信号而言，发生了相移；二是滤波后的信号在起始部分，波形畸变较为严重。在信号处理中，如果对信号的相位有特殊的要求，相移问题需要引起高度的注意。而起始部分的畸变是由于叠代过程中，没有考虑滤波器的初始条件，刚开始点数少，没能用到滤波器全部系数的缘故。大多情况下，这种畸变可以接受，但当数据较短，而滤波器的阶数又较高时，这种畸变会带来较大的负面影响。

　　如果输入信号为一单位脉冲信号，即

　　x（n）=1，n=1

　　0，n≠1

　　那么，滤波器的输出为其脉冲响应。本文所用200阶FIR低通数字滤波器的脉冲响应如图5所示。

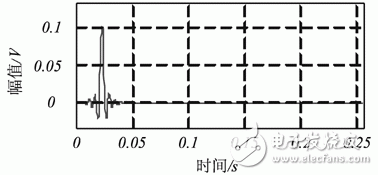
　　图5滤波器的脉冲响应3零相位数字滤波算法及其实现

　　3.1 零相位数字滤波的算法

　　为了克服差分数字滤波中存在的上述两个问题，可以采用一种零相位滤波的方法，该方法的基本思路是：先确定出滤波器的初始条件，然后将原序列的首尾进行扩展，把扩展后序列通过滤波器，将所得结果反转后再次通过滤波器，最后将所得结果再反转，并去掉首尾的扩展部分，即可得到零相位滤波后的输出序列。本文采用四次差分滤波方式给出一种便于实现的详细算法，假设输入信号为x（n），n=0，1，…，P.

　　（1） 编写差分滤波函数DiffFilter（b，a，x），调用参数如前所述。

　　（2） 对于IIR滤波器通常有M=N，求滤波器的初始条件e（q），q=0，1，…，N-1，这里记E=［e（0），e（1），…，e（N-1）］T，则有

　　E=1+a（1）1-1…0

　　a（2）01…0

　　MMMOM

　　a（N）00…-11× b（1）-b（0）a（0）

　　b（2）-b（0）a（1）

　　M

　　b（Nn）-b（0）a（N）（3）

　　（3） 对原输入序列x（n）的首尾进行扩展，在x（n）的前面添加3N个数，在后面添加3N个数，扩展后的序列记为x′（n），n=0，1，…，P+6N.

　　x′（n）=2x（0）-x（3N-n）

　　x（n-3N）

　　2x（P）-x（P-1-（n-P-3N-n））

　　n<3N

　　3N?n《P+3N

　　P+3N?n?P+6N（4）

　　（4） 进行正向滤波：先用b，a和x′（n）调用DiffFilter（b，a，x）函数，计算x′（n）通过

　　H（z）=∑Mm=0b（m）z-m/（1+∑Mm=1a（m）z-m）（5）

　　的输出y′（n），然后生成一长度为P+6N+1的单位脉冲信号h（n），用z，a和h（n）调用DiffFilter（b，a，x）函数，计算h（n）通过

　　H（z）=∑M-1m=0y′（0）e（m）z-m/（1+∑Mm=1a（m）z-m）（6）

　　的输出y′（n），并记y（n）=y′（n）+y″（n）。

　　（5） 进行反向滤波：将正向滤波结果反转，记x′（n）=y（P+6N-n），重复步骤4°，得到反向滤波后的结果。

　　（6） 将反向滤波的结果反转，并删除首尾的扩展部分，即可得到最后的滤波结果。

　　3.2 零相位数字滤波的实现

　　Borland公司推出的Delphi编程语言，具有合理的单元化结构、优化的编译环境，开发速度快、编程效率高。在实现同样功能的情况下与其它语言相比，不仅编写的代码量少、程序可移植性强，而且还有许多优秀的组件包可供使用。最为方便的是可以使用动态数组，随时能够改变数组的长度，这一点非常适合数字信号处理。

　　作者利用Delphi7编写了利用双线性Z变换法设计Butterworth型IIR滤波器和利用窗函数法设计FIR滤波器，以及差分数字滤波算法和零相位数字滤波算法应用程序，并作为集成测试软件平台的一个虚拟仪器。其中零相位数字滤波算法程序设计流程如图6所示。

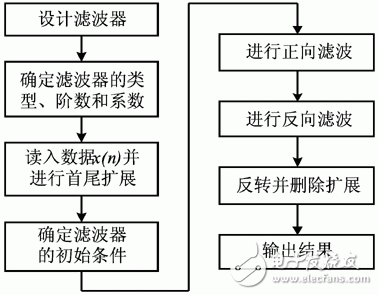
　　图6零相位数字滤波算法的流程图

图7所示为图2所示信号零相位数字滤波后的波形，通过与原信号（图2）和差分滤波后的信号（图 4）对比不难看出：零相位数字滤波后的输出与原信号中的相位基本一致，并且起始部分没有畸变。但不可否认，零相位数字滤波算法相对于普通差分滤波算法计算量要大许多，但以目前计算机