理解ADC误差对系统性能的影响

虽说不被作为一项关键性的ADC参数，微分非线性（DNL）误差还是进入我们视野的第一项指标。DNL揭示了一个输出码与其相邻码之间的间隔。这个间隔通过测量输入电压的幅度变化，然后转换为以LSB为单位后得到（图1）。值得注意的是INL是DNL的积分，这就是为什么DNL没有被我们看作关键参数的原因所在。一个性能优良的ADC常常声称"无丢码"。这就是说当输入电压扫过输入范围时，所有输出码组合都会依次出现在转换器输出端。当DNL误差小于±1LSB时就能够保证没有丢码（图1a）。图1b、图1c和图1d分别显示了三种DNL误差值。DNL为-0.5LSB时（图1b），器件保证没有丢码。若该误差值等于-1LSB （图1c），器件就不能保证没有丢码，值得注意的是10码丢失。然而，当最大DNL误差值为±1时，大多数ADC都会特别声明是否有丢码。由于制造时的测试界限实际上要比规格书中所规定的更为严格，因此这种情况下通常都能够保证没有丢码。对于一个大于-1LSB （图1d中为-1.5LSB）的DNL，器件就会有丢码。

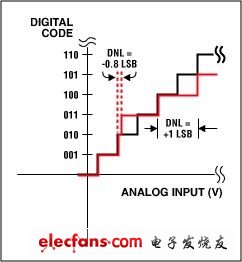
图1a. DNL误差：没有丢码。

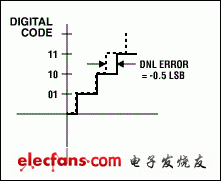
图1b. DNL误差：没有丢码。

图1c. DNL误差：丢失10码。

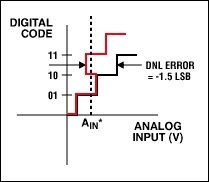
图1d. DNL误差：AIN*数字输入是三种可能数值之一，扫描到输入电压时，10码将会丢失。

随着DNL误差值的偏移（也就是说-1LSB，+2LSB），ADC转换函数会发生变化。偏移了的DNL值理论上仍然可以没有丢码。关键是要以-1LSB作为底限。值得注意的是DNL在一个方向上进行测量，通常是沿着转换函数向上走。将造成码［N］跳变所需的输入电压值和码［N+1］时相比较。如果相差为1LSB，DNL误差就为零。如果大于1LSB，则DNL误差为正值；如果小于1LSB，DNL误差则为负值。

有丢码并非一定是坏事。如果你只需要13位分辨率，同时你有两种选择，一个是DNL指标≤ ±4LSB的16位ADC （相当于无丢码的14位），价格为5美元，另一个是DNL ≤ ±1LSB的16位ADC，价格为15美元，这时候，购买一个低等级的ADC将大幅度地节省你的元件成本，同时又满足了你的系统要求。

积分非线性

积分非线性（INL）定义为DNL误差的积分，因此较好的INL指标意味着较好的DNL。INL误差告诉设计者转换器测量结果距离理想转换函数值有多远。继续我们的举例，对于一个12位系统来讲，±2LSB的INL误差相当于2/4096或0.05%的最大非线性误差（这已占去ADC误差预算的2/3）。因此，有必要选用一个1LSB （或更好）的器件。对于±1LSB的INL误差，等效精度为0.0244%，占ADC误差预算的32.5%。对于0.5LSB的指标，精度为0.012%，仅占ADC误差预算的16% （0.0125%/0.075%）。需要注意的是，无论是INL或DNL带来的误差，都不太容易校准或修正。

失调和增益误差

失调和增益误差很容易利用微控制器（μC）或数字信号处理器（DSP）修正过来。就失调误差来讲，如果转换器允许双极性输入信号的话，操作将非常简单。对于双极性系统，失调误差只是平移了转换函数，但没有减少可用编码的数量（图2）。有两套方法可以使双极性误差归零。其一，你可以将转换函数的x或y轴平移，使负满度点与单极性系统的零点相对准（图3a）。利用这种方法，可以简单地消除失调误差，然后，通过围绕"新"零点旋转转换函数可以对增益误差进行调节。第二种技术采用了一种迭代法。首先给ADC输入施加一个0V电压并执行一次转换；转换结果反映了双极性零点失调误差。然后，通过围绕负满度点旋转转换曲线实现增益调节（图3b）。注意此时转换函数已绕A点转过一定角度，使零点偏离了期望的转换函数。因此还需要进一步的失调误差校正。

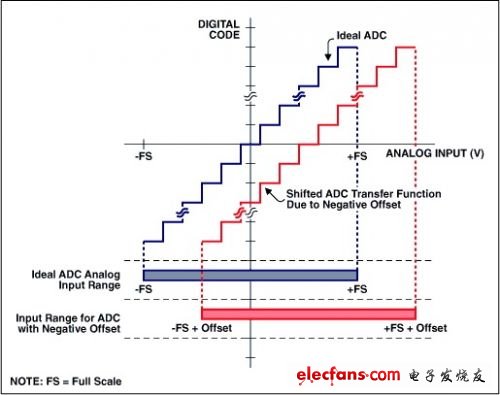
图2. 双极性系统的失调误差

图3a和3b. 校正双极性失调误差（注意：阶梯状转换函数已被一条直线取代，因为该图中包含所有码，而台阶已经小得无法分辨，看上去成为一条直线）。

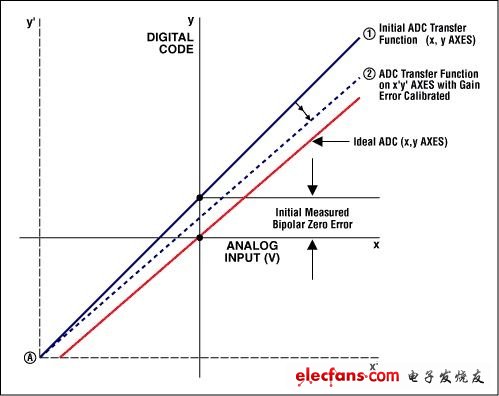
图3a和3b. 校正双极性失调误差（注意：阶梯状转换函数已被一条直线取代，因为该图中包含所有码，而台阶已经小得无法分辨，看上去成为一条直线）。

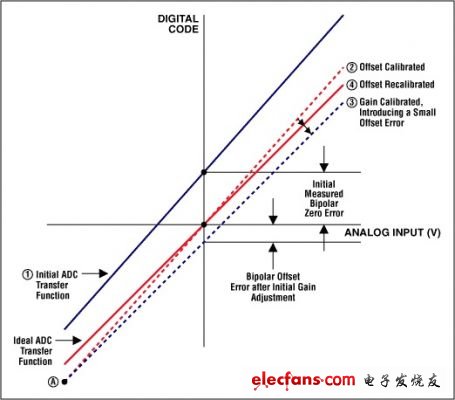
图3a和3b. 校正双极性失调误差（注意：阶梯状转换函数已被一条直线取代，因为该图中包含所有码，而台阶已经小得无法分辨，看上去成为一条直线）。

单极性系统还要复杂一些。如果失调为正值，可采用和双极性系统相似的处理方法。不同之处在于你将失去一部分ADC量程（见图4）。如果失调为负值，你将无法简单地通过一次转换测得失调误差。因为在零点以下，转换器只能显示出零。这样，对于一个负失调误差的转换器，你必须缓慢地增加输入电压，以确定在什么地方ADC结果出