传导式EMI的测量技术解析

　　利用简单的数学公式，就可以将于L和N线路上所测得的电流，区分为CM电流和DM电流。但是为了避免发生代数计算的错误，必须先对电流的「正方向」做一定义。可以假设若电流由右至左流动，就是正方向，反之则为负方向。此外，必须记住的是：一个电流I若在任一线路中往一个方向流动时，这是等同于I往另一个方向流动的（Kirchhoff定律）。

　　例如：假设在一条线路（L或N）上，测得一个由右至左流动的电流2μA。并在另一条线路上，测得一个由左至右流动的电流5μA。CM电流和DM电流是多少呢？就CM电路而言，假设它的E连接到一个大型的金属接地平面，因此无法测量出流过E的电流值（如果可以测得，那将是简单的Icm）。这和一般离线的（off-line）电源供应器具有3条（有接地线）或2条（没有接地线）电线不同，我们将会发现对那些接地不明的设备而言，其实它们具有一些泄漏（返回）路径。

　　以图一为例，假设第一次测量的线路是L（若选择N为首次测量的线路，底下所计算出来的结果也是一样的）。由此可以导出：

　　IL = Icm/2 + Idm= 2μA

　　IN = Icm/2 - Idm= -5μA

　　求解上面的联立方程式，可以得出：

　　Icm = -3μA

　　Idm = 3.5μA

　　这表示有一个3μA的电流，流过E（这是共模的定义）。而且，有一个3.5μA的电流在L和N线路中来回流动。

　　再举一个例子：假设测得一个2μA的电流在一条线路中由右至左流动，而且在另一条线路中没有电流存在，此时，CM电流和DM电流为多少？

　　IL = Icm/2 + Idm= 2μA

　　IN = Icm/2 - Idm= 0μA

　　对上面的联立方程式求解，可得出：

　　Icm = 2μA

　　Idm = 1μA

　　这是「非对称模式」的例子。从此结果可以看出，「非对称模式」的一部分可以视为「不对称（CM）模式」，而它的另一部分可视为「对称（DM）模式」。

　　传导式EMI的测量

　　为了要测量CE，我们必须使用线路阻抗稳定网络（Line Impedance Stabilization Network；LISN）。如图三所示一个简易的LISN电路图。

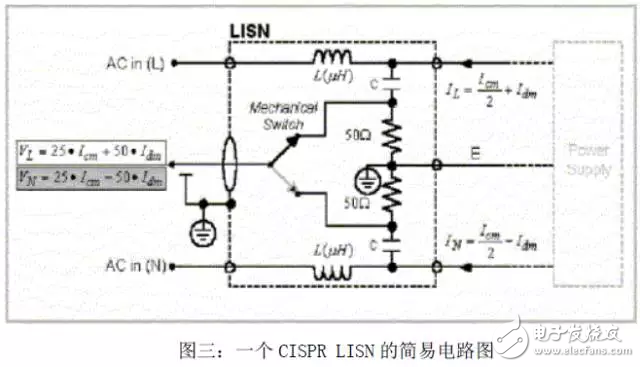
　　使用LISN的目的是多重的。它是一个「干净的」交流电源，将电能供应给电源供应器。接收机或频谱分析仪可以利用它来读出测量值。它提供一个稳定的均衡阻抗，即使噪声是来自于电源供应器。最重要的是，它允许测量工作可以在任何地点重复进行。对噪声源而言，LISN就是它的负载。假设在此LISN电路中，L 和C的值是这样决定的： 电感L小到不会降低交流的电源电流（50/60Hz）；但在期望的频率范围内（150 kHz to 30MHz），它大到可以被视为「开路（open）」。电容C小到可以阻隔交流的电源电压；但在期望的频率范围内，它大到变成「短路（short）」。

　　在图三中，主要的简化部分是，缆线或接收机的输入阻抗已经被包含进去了。测量传导时，将一条典型的同轴缆线连接到一台测量仪器（分析仪或接收机或示波器…等）时，对一个高频讯号而言，此缆线的输入阻抗是50欧姆（因为传输线效应）。所以，当接收机正在测量这个讯号时，假设在L和E之间，LISN使用一个「继电/切换（relay/switch）电路」，将实际的50欧姆电阻移往相反的配对线路上，也就是在N和E之间。如此就能使所有的线路在任何时候都能保持均衡，不管是测量VL或VN。

　　选择50欧姆是为了要仿真高频讯号的输入阻抗，因为高频讯号所使用的主要导线之阻抗值近似于50欧姆。此外，它可以让一般的测量工作，在任何地点、任何时间重复地进行。值得注意的是，电信设备的通讯端口是使用「阻抗稳定网络」，它是使用150欧姆，而不是50欧姆；这是因为一般的「数据线路（data line）」之输入阻抗值近似于150欧姆。

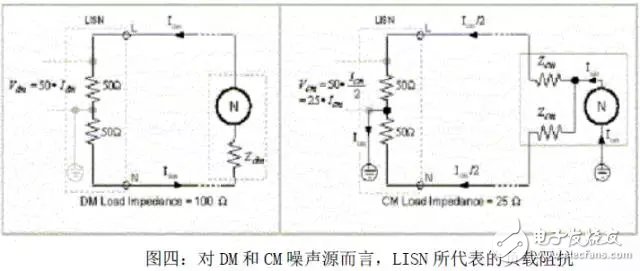
　　为了了解VL和VN，请参考图四。共模电压是25Ω乘以流向E的电流值（或者是50Ω乘以Icm/2）。差模电压是100Ω乘以差模电流。因此，LISN提供下列的负载阻抗给噪声源（没有任何的输入滤波器存在）：

　　CM负载阻抗是25Ω，DM负载阻抗是100Ω。

　　当LISN切换时，可以由下式得出噪声电压值：

　　VL=25*Icm+50*Idm 或 VN=25*Icm – 50*Idm

　　这是否意味着只要在L-E和N-E上做测量，就可以知道CM和DM噪声的相对比例大小？

其实，许多人常有这样的错误观念：「如果来自于电源供应器的噪声大部分是属于DM的，则VL和VN的大小将会相等。如果噪声是属于CM的，则VL和VN的大小也会相等。但是，如果CM和DM的辐射大小几乎相等时，则VL和VN的测量值