滤波器功率与灵敏度矛盾解决方法

采用适当的组件值的情况下，我们可以让所有功率在特定的频率上全部到达负载上，而不用管负载的值是多少。

　　如果我们可以使用变压器或者变压器的等效LC线路，我们可以计算出50欧姆信源和3.3K欧姆负载之间能够获得的最大电压增益。需要的电压变换等于阻抗比的平方根，在本例中为8.12倍。将该比例与我们在等电阻端接例子中的电压增益0.5相乘。所以在任意LC值下可以得到的最大增益为4.06 倍，或者大约12.2dB。图10显示的是用我们自制的变压器任意选择1,000种不同的L和C值得到的结果。响应曲线的峰值从未超过预计值。至于为什么不是每个频率下所有功率都耗散在负载上，是因为部分功率被反射回了信源。　　

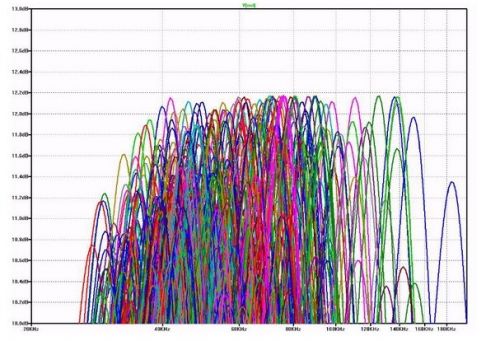
图10：响应曲线的峰值从未超过预计值

　　所有射频工程师都开始不耐烦地打哈欠了，因为这是你们的常识。设计LC网络，确保让所有信源的功率传输到负载，是一项称之为阻抗匹配的核心射频技术。这确实像两个不等电阻之间的滤波器设计(每种设计方案都有其伴随的虚部需要加以考虑)。一般是用L和C来完成的，而非体积庞大、成本高昂的变压器。除微波频段外，其中的变压器体积不大、价格也不高，不过当导体靠得太近的时候，会造成谐振波峰。

　　现在回到我们最初讨论的问题。为什么一个(设计合理的)双端接滤波器有如此出色的"灵敏度"属性?这是因为对滤波器通带内的一个或者有时多个频率，它工作在功率传输的最大可能点上。请再次观察图6和图7。在双端接滤波器情况下，组件值的任何变化只会让功率传输(随之为电压增益)下降而非上升。在被称之为反射零点的特定关键频率上，滤波器响应的"灵敏度"与网络中每个无功部分呈抛物线函数的下行段关系。这样就很难让网络的响应比没有应用功率传输约束的时候更差。后者状况指的是单端接的时候，或者任何滤波器的设计响应未能满足最大功率增益值的时候。要得到最大功率增益值，可以抛开滤波器，使用变压比较为合适的理想变压器。

　　还有一个问题。我们在开始的时候曾经比较过两种滤波器，其中一种滤波器的负载电阻与信源电阻相等，另一个则没有负载电阻。我们能否在尽可能大的给定信源电阻和负载电阻比率下成功设计出低灵敏度、等频率响应的滤波器?有时候是可以的，但具体到我们的低通滤波器则不能。对于具体的响应，我们要求平坦的响应，让DC增益与那些"触点"最大值相等。这就意味着在该极低灵敏度滤波器中，信源电阻和负载电阻必须等值。对于更加普遍的情况，如果不需要对通过的 0频率或者无穷频率施加特定的衰减，通常可以设计出任意两个阻抗间的最低灵敏度(即理想匹配)滤波器。至于如何实现，足够写上几本书，不过初学者就不用看了。