SIW带通滤波器仿真设计

　0 引言

　　滤波器在无线通信、军事、科技等领域有着广泛的应用。而微波毫米波电路技术的发展，更加要求这些滤波器应具有低插入损耗、结构紧凑、体积小、质量轻、成本低的特点。传统用来做滤波器的矩形波导和微带线已经很难达到这个要求。而基片集成波导(SIW)技术为设计这种滤波器提供了一种很好的选择。

　　SIW的双膜谐振器具有一对简并模式，可以通过对谐振器加入微扰单元来使这两个简并模式分离，因此，经过扰动后的谐振器可以看作一个双调谐电路。分离的简并模式产生耦合后，会产生两个极点和一个零点。所以，双膜滤波器在减小尺寸的同时，也增加了阻带衰减。而且还可以实现较窄的百分比带宽。可是，双膜滤波器又有功率损耗高、插入损耗大的缺点。为此，本文提出了一种新型SIW腔体双膜滤波器的设计方法。

　　该SIW的大功率容量、低插入损耗特性正好可以对双膜滤波器的固有缺点起到补偿作用。而且输入／输出采用直接过渡的转换结构，也减少了耦合缝隙的损耗。

　　l 双膜谐振原理及频率调节

　　SIW是一类新型的人工集成波导，它是通过在平面电路的介质层中嵌入两排金属化孔构成的，这两排金属化孔构成了波导的窄壁，图1所示是基片集成波导的结构示意图。这类平面波导不仅容易与微波集成电路(MIC)以及单片微波集成电路(MMIC)集成，而且，SIW还继承了传统矩形波导的品质因数高、辐射损耗小、便于设计等优点。

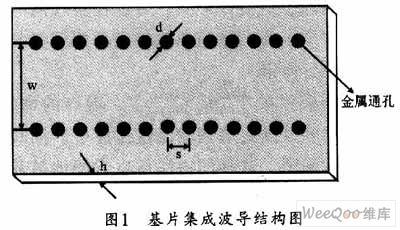
1．1 基片集成波导谐振腔

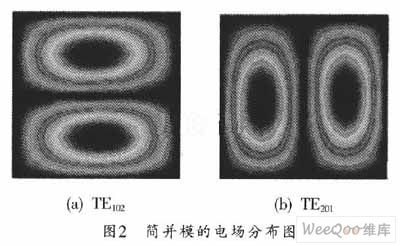
　　一般情况下，两个电路的振荡频率越接近，这两个电路之间的能量转换需要的耦合就越小。由于谐振腔中的无数多个模式中存在着正交关系，故要让这些模式耦合发生能量交换，必须对理想的结构加扰动。但是，为了保持场结构的原有形式，这个扰动要很小。所以，本文选择了SIW的简并主模TE102和 TE201，它们的电场分布图如图2所示。因为TM和TEmn(n10)不能够在SIW中传输。因此，一方面可以保证在小扰动时就可以实现耦合，同时也可以保证场的原有结构。

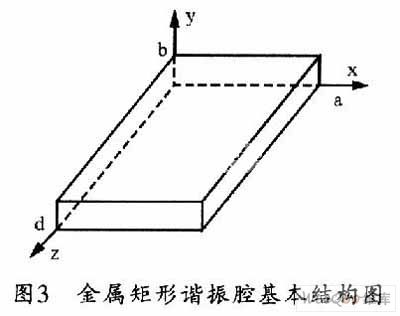
假设图3所示的矩形腔体的长、宽、高分别为a、b、d。因为TEmn(n10)不能在SIW中传输，所以对于SIW谐振腔来说，其谐振频率的计算公

　　式如下：

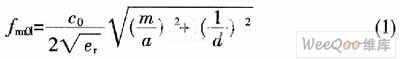
　　对于具有相同谐振频率的两个模式来说，则有如下关系：

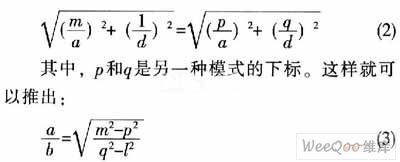
选定的工作简并模式，利用公式(1)、(2)、 (3)来确定矩形波导谐振腔的初始尺寸，然后再结合有关文献，就可以确定SIW腔体的尺寸。图3所示是其金属矩形谐振腔的基本结构。

　　1．2 双膜SIW谐振腔及其频率调节

　　圆柱形波导、矩形波导和微带线都可以用来做双膜滤波器。然而，一些典型的双膜设计方法(如加调节螺钉、内角加工、在微带贴片上加入十字槽等)并不适用于SIW腔体。有文献提到采用切角、打孔、馈电扰动等扰动方式来应用于SIW腔体。故此，本文选取了在SIW腔体对称的角上切两个相同的方形切角作为微扰方式。扰动腔体的谐振频率被分成f1和f2两个高低不同的频率，这两个频率的平均值(f1+f2)／2和原有腔体的谐振频率f0往往不相等。类似地，输入／输出部分的耦合也会造成谐振频率的平移。这样就会造成两种情况：一是(f1+f2)／2>f0；二是(f1+f2)／2< P>

　　是大于还是小于取决于耦合结构。对于第一种情况，可以通过加大谐振腔尺寸来调节频率移动；而对于第二种情况，则可以通过减小谐振器尺寸或者在谐振腔上开个缝来减少谐振腔等效尺寸等方法来调节。当然也可以不调节，分别针对这两种情况加以利用。在实际的工程应用中。要求 s<λ／20，当SIW工作在高频段时，为了满足上述条件，往往要求金属柱半径以及它们之间的间距很小，以至于加工非常困难。而此时就可以利用第一种情况，以较大的尺寸在较高频率处实现良好的滤波性能，降低加工难度；而对于第二种情况，可以以更小的尺寸在较低的谐振频率处实现良好的滤波性能，从而实现滤波器的小型化。本文就是有效地利用了第二种情况，从而设计出性能好、尺寸小的滤波器。

　　2 双膜滤波器的实现与仿真

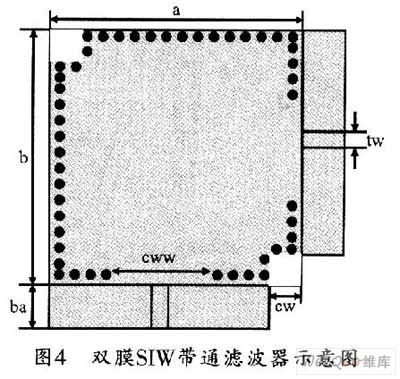
　　图4所示是双膜SIW腔体带通滤波器的结构示意图。在谐振腔的对角线上挖去两个相同的立方体，输入／输出采用直接过渡的转换结构。滤波器选用 Rogers RO3010作为介质基板，其相对介电常数εr=10．2，损耗角正切tan d为0．0035；谐振腔长度a为21．5 mm，宽b为21．5 mm，高h为0．5mm；切去的立方体边长cw为2．2 mm；中心馈线的宽度tw为0．72 mm。输入／输出采用无缝耦合的直接转换结构，这样可减少输入／输出结构的耦合损耗。

3 仿真结果分析

仿真可采用电磁仿真商业软件HFSS来完成。通过仿真介质谐振腔滤波器(滤波器源型)可以发现，不同的耦合输入／输出窗口宽度影响着滤波器中心频率的位置，同时