模数混合型FIR噪声滤波器设计

相位偏移△φi。

　　考虑到这些因素后，式(2)所示的FIR滤波器传递函数将转变为：

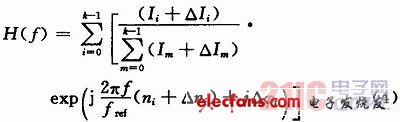
　　其中，作为模拟模块的电荷泵，电流镜失配引起的各支路电流的改变是不可避免的，因此是影响FIR滤波器传递系数的主要因素。通过在上电初始化时对并行各支路加以同步复位后影响因素(3)，将与影响因素(2)一样，由于相关的电路模块为寄存器链、分频器以及鉴频鉴相器等离散时间域工作的数字模块，因此主要受时钟抖动影响，从而相对△Ii而言，△ni和△φi可以忽略。

　　基于以上考虑，假设电流失配、延时失配以及非同步引起的附加相差分别满足3σ=15%，3σ=1%和3σ=0.01π的正态分布。对由式(3)给出的混合型FIR滤波器的频域响应做Monte-Carlo分析，可以得到如图6所示的结果。

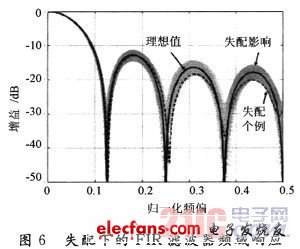
　　对于其他纯模拟的量化噪声抑制技术，比如采用数/模转换器补偿量化误差的方法，失配将造成整个频带上噪声抑制效果的恶化。从图6可以看到，混合型FIR噪声滤除技术中，失配主要影响传递函数的零点位置。在远离零点的频偏处，滤波器增益的变化在±3 dB以内;而在预期的零点位置处，即便有失配存在，仍然能保证有至少25 dB的抑制，这通常已经足以把量化噪声降低到不再影响整体性能的水平。此外，从图中虚线给出的不失一般性的个例可以看到，尽管失配使得在一些频偏处的噪声抑制程度不如预期值，但也使得在其他频偏处的噪声抑制要优于预期值。这个特性进一步使得量化噪声的总体改善对失配不敏感。

　　3 并行支路间的准同步

　　传统△-∑锁相环或△-∑延时锁定环中只有一个鉴相器，其输入端的参考时钟和环路反馈回来的信号时钟之间在锁定后只存在由式(4)给出的瞬时相位误差，这决定了电荷泵的开启时间和对应的噪声注入。而在采用混合型FIR噪声滤除技术的结构中，存在并行多支路鉴相器。它们一方面共享同一个参考时钟，另一方面则是由各自对应的分频器或相位选择器产生各自的信号时钟，因此存在是否需要对这些信号时钟加以同步的问题。

　　支路间处于异步状态时将造成的问题如图7所示。

　　为不失一般性，此处假设要实现一个简单的2抽头FIR滤波器，其传递函数为(1+z-1)/2，因此环路中将需要用到2个支路的鉴相器。如图7所示，在环路建立后，参考时钟沿将被锁定在2个信号时钟沿的中间。因此，如果两个信号时钟沿的相位差为△φ，则对于每个鉴相器而言，输入端的瞬时相位误差比原来增加了△φ/2。此外，为了保持环路的锁定，2个电荷泵支路需要在每个鉴相周期内交替充放电。支路间的相位差△φ越大，也就意味着电荷泵开启时阊以及噪声注入时间越长，从而严重恶化带内相位噪声以及参考杂散性能。另一方面，支路间异步引入的附加相位偏移还将影响所要实现的混合型FIR滤波器的传递函数。

　　为了避免这些性能上的恶化，混合型FIR噪声滤除技术在电路实现上需要保证并行支路间处于准同步状态，即各信号时钟的相位差应满足：
　

　　式中：φi和φj分别为第i和j路信号相位;Ni和Nj为支路对应的控制字;φstep为相位量化步长。可见，这里的“准同步”包含2个含义：一方面，由于各支路的信号时钟受控于不同的控制字，因此不可能实现零相位差的完全同步;另一方面，各支路信号时钟的相位差应当仅由量化控制字的差异引起，无任何附加相位差。

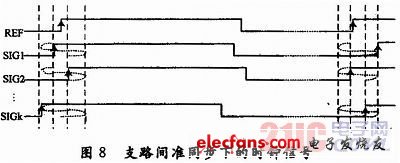
　　图8是4电平量化下支路准同步后的时钟信号示例。各支路信号时钟在同样的4个备选相位间切换，从而对于任何一个支路而言，其工作状态都和传统结构完全一致，这就实现了真正意义上并行操作和离散时间域的信号合成。

　　就电荷泵本身而言，由于其总电流与传统结构一致，这使得所用的有源器件总体尺寸保持不变，从而贡献的噪声也就不变。惟一的差别是多输入电荷泵中需要多用若干个开关管，其带来的噪声恶化几乎可以忽略。

     4 电荷泵非线性的改善

　　在△-∑锁相环或△-∑延时锁定环里，电荷泵的非线性将造成高频量化噪声被折叠到低频，从而影响带内相位噪声性能。采用了混合型FIR噪声滤除技术后，由于环路中并行的鉴相器和电荷泵支路是由△-∑调制器的输出经过不同时钟周期延时后依次控制的，因此会对各支路受数字控制的相位误差有类似“桶形移位”的效果。如图9所示，尽管该结构没有像模/数转换器设计中的桶形移位技术一样存在控制字的卷绕，但多支路的并行工作配合依序的控制，使得所有相位误差电荷在电荷泵中合成后，各支路数控相位到模拟域电荷的非线性映射可以得到平均和改善。

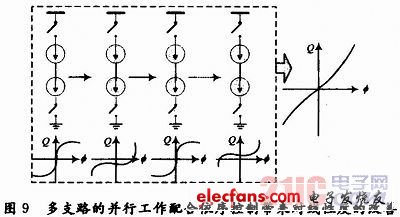
这种结构对电荷泵非线性的改善还可以从另一个角度来解释，即造成电荷泵非线性的一个重要原因是其上下电流存在和输出电