详解LED灯具的功率因数

因数

　　我们知道白炽灯因为是一个纯电阻，它的功率因数当然等于1。但是使用越来越多的日光灯和最近国家大力推广的节能灯就不是这样了。长期以来，日光灯都是用一个大电感和一个起辉器来启动。点亮以后大电感就串联在电路里，所以它基本上是一个感性负载，它的功率因数只有0.51-0.56。以后改用电子镇流器，功率因数要好一些，但是因为电子镇流器很容易烧毁，所以用得最多的还是电感镇流器。

　　而节能灯的功率因数也是只有0.54左右，而且也是感性负载。

　　四。 LED灯具的功率因数

　　因为LED是一个半导体二极管，它需要直流供电，如果用市电供电的话，就一定会有一个整流器，通常是二极管整流桥。为了得到尽可能平滑的直流避免出现纹波闪烁，通常都需要加上一个大电解电容。而后面的LED可以近似为一个电阻，所以整个电路如图3所示。

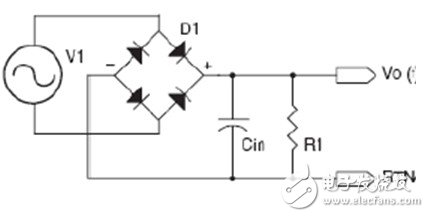
　　图3. LED灯具的等效电路

　　其各种电流电压如图4所示。

　　【字体：大 中 小】

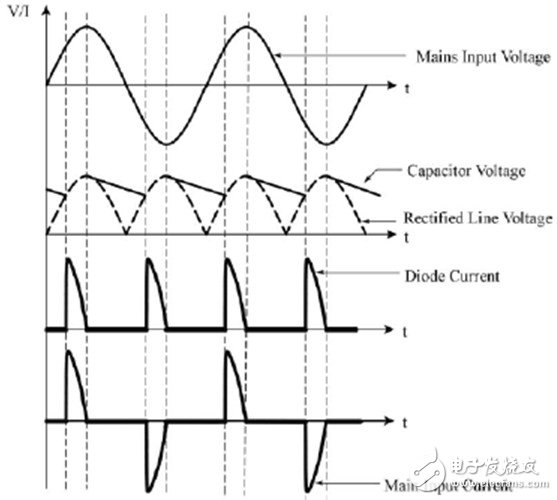
　　图4. 桥式整流加电容滤波后的电压电流波形

　　整流后的电压电流波形都不是正弦波，而且虽然整流前的电压波形是正弦波，但是其电流波形也不是正弦波。所以整个系统是一个非线性系统。而本来功率因数是针对线性系统定义的，而且要求输入输出电压电流都是同频率的正弦形，否则的话无法采用Cosφ。但是在非正弦系统中，因为电压电流波形都不是正弦波，是没有什么相位角可以说的。所以非线性系统中的功率因数必须重新定义。

　　如前所述功率因数的另一个定义是有功功率和视在功率之比。有功功率是指实际输出的功率，而视在功率是指输入电压有效值和输入电流有效值的乘积。这个在正弦波系统里是完全可以和Cosφ等效的，所以是没有问题的。但是在非线性系统里，什么是有功功率什么是视在功率就很值得探讨的了。

　　因为在非线性系统里，其电流波形有很多高次谐波（见图5），

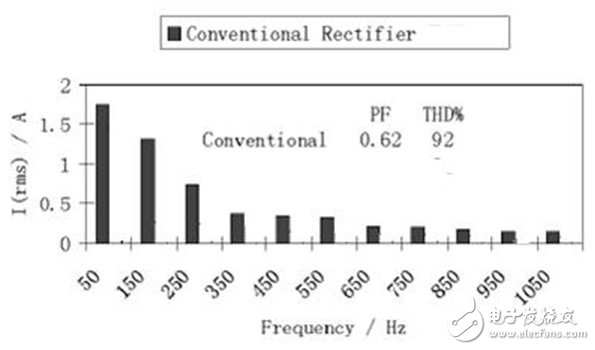
　　图5. 普通桥式整流器的电流高次谐波

　　所以到底拿什么来作为其视在功率，就是一个很大的问题。现在有各种做法。

　　1. 将电流的基波有效值和正弦电压有效值相乘来作为其视在功率，或是把基波电流相位的余弦作为功率因数，或是把电流波形的过零点相位的余弦作为功率因素。有些仪器就是这样来测量的。由这个电流的波形图中就可以看出，这种波形的高次谐波非常丰富，其基波很小，如果用基波电流来乘基波电压，那么是得到的功率相比有功功率就很小，这样它的功率因数就会很高甚至有可能大于1。

　　例如在一些指针式的功率因素计就是如此。

　　2. 采用电压的有效值和电流的有效值相乘来作为视在功率。

　　现在很多数字式功率因数仪是采用电压有效值和电流有效值的乘积来作为视在功率的。

　　对于非正弦波电流的有效值可以用各次谐波电流的均方根值来表示：

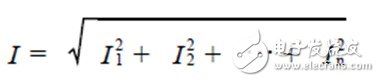
　　如果定义功率因数等于实际功率和视在功率之比

　　通常把谐波失真定义为：

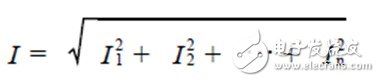
　　现在的很多数字式功率因素计基本上都是用这种方法来定义的。

　　但是功率的定义必须是相同频率正弦波的电压有效值和电流有效值的乘积。电流高次谐波有效值和基波电压有效值的乘积不能认为是功率，因为其频率不一样，所以是没有意义的数字。所以用这种方法来定义视在功率是有问题的。遗憾的是，现在很多数字仪表都是这样来测量的。

　　实际上，这个问题在学术界是一直存在争议的，所以美国的硕士论文和瑞典的博士论文都还在研究这个问题。

　　例如瑞典的Stefan Svensson在他的博士论文里就指出，在非线性的情况下，现在对于功率因数就已经有人提出了7种不同的定义，同样一个非线性系统在不同的定义下，就可能得出完全不同的功率因数值。而且不管是哪种定义它都不符合当初在线性系统里提出功率因数的初衷。例如。在线性系统里，只要采用纯电容或纯电感就可以补偿感性或容性的负载。这在非线性系统里显然是无效的。所以这些定义的功率因数完全失去了原来功率因数的含义。

　　其实，在非线性负载时，最大的问题是谐波电流，因为虽然谐波电流不能和基波电压形成视在功率，但是谐波电流的平方乘以线路电阻就会引起热损耗。而且这种谐波电流是无法采用简单的电容或电感加以补偿的。所以真正需要限制的是谐波电流值。而不是所谓的"功率因数"。

　　五。 现在的有关规定是否合理

就算我们接受现有的普通功率因数测量仪所测得的LED灯具的功率因数值，但是到底是多少是允许的。按照美国能源之星规定凡是功率小于5瓦的LED灯具不要求功率因数。而大于5瓦则要求功率因数必须高于0.7。中国现在采用和美国一样的规定。但深圳市LED产业标准联盟的标准规定《10W，