基于 GNU Radio 和 USRP 的频谱检测方法
时间:12-17
来源:新浪科技
点击:
1 频谱检测方法介绍
1.1 认知无线电频谱感知原理
目前,在认知无线电领域用于检测某频段内是否有信号存在、有哪些信号存在的方法有多种。以检测类型划分,可分为信号存在性检测和信号覆盖范围检测两类;以检测节点个数划分,可分为单节点检测和多节点联合检测;以检测方法划分,主要分为匹配滤波、能量检测、周期特性检测三类[23]。总结归纳各种方法如图所示:
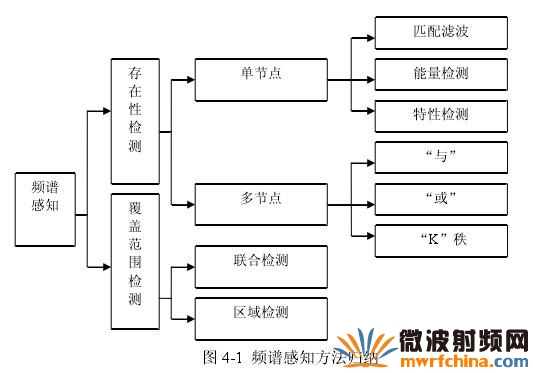
信号存在检测,是指在经过对某特定频段内信号的进行观测之后,做出该频段上是否有信号存在的判断,这种探测原理的基本模型可以用下面的公式表示:
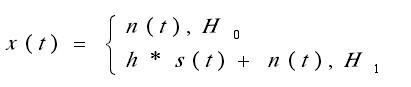
其中,x(t)是认知无线电接收到的信号,s(t)是第一用户传输的信号;n(t)是加性白高斯噪声;h 是信道的增益;Ho 是未被占用的假设,表明了目前在这一确定频段上没有第一用户;H1 是另一种假设,表明目前存在第一用户。
下面将对单节点检测的几种方法进行介绍、分析:
(1)匹配滤波器探测
当认知无线电获悉了第一用户的信号后,静态高斯噪声理想探测器就是匹配滤波器,原因在于它能使接收到的信号的信噪比(SNR)最大化。匹配滤波器的主要优点是它只需很短的时间就可以获得高处理增益。然而,它必须有效地对第一用户的信号进行解调,这就意味着它需要第一用户的先验知识,比如解调方式和阶数、数据包格式等。
上述信息可以预存在认知无线电的内存中,然而,对解调来讲,认知无线电必须通过时间和载频同步甚至信道同步来获得第一用户的相关性。如果这些信息是不准确的,那么,匹配滤波器的性能就会变得很差。匹配滤波器探测的一个明显缺点在于,认知无线电对每一类型的第一用户都要有一个专门的接收器。
(2)能量探测
如果接收机不能够收集到第一用户信号的足够的信息,此时的最佳探测器就是能量探测器。为了测量接收信号的能量,需要对带宽为 W 的带通滤波器的输出信号进行平方运算并在观测时间段 T 内进行积分,并将积分器的输出 Y 与门限值进行比较,从而判定合法用户是否出现。检测过程示意图如下所示:
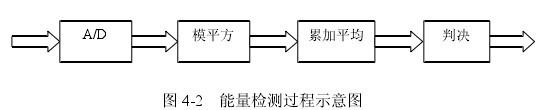
能量探测器的门限很容易受到噪声功率的变化的影响。为了解决这个问题,已经有文献提出通过第一用户发射机的导频音(Pilot Tone)来提高认知无线电能量探测器的准确性。另外,即使能够适应性的设定门限值,带内干扰的出现也会扰乱能量探测器。能量探测器的另外一个缺点是它只能探测到有用信号出现,而不能够区分信号的类型,即它不能区分已调制信号 、噪声及干扰。因此,能量探测器容易被不明信号误导而产生误判决。
(3)静态循环特征探测
调制信号一般都经过了载波、脉冲序列、重复性扩展、跳频及循环前缀等耦合处理,使已调信号具有了内在的周期性。虽然数据是静态随机的,但是这些调制后的信号的均值和自相关函数都具有周期性,因而称其具有循环性。通过分析频谱自相关函数可以探测出这些特征。频谱自相关函数的最主要的优点是它能够把噪声能量和已调信号的能量区分开来,这是因为噪声是一个宽带的、静态的、没有相关性的信号,而已调信号具有频谱相关性和周期性。静态循环特征探测器具有更强的抵抗噪声功率中不确定性的能力,因而能够比能量探测器更好地分辨出噪声信号。不过,它就比能量探测器更加复杂并且需要更长的观测时间。
4.1.2 感知任务
综合比较上述三种检测方法的优缺点,我们可以得到下面的对比:

在本认知无线电实验平台中,我们选择能量检测的方式做频谱感知。因为匹配滤波需要授权用户的信号模型,只能针对某种信号进行检测,而能量检测的方法对任意信号都适用。而且匹配滤波需要重构到某种调制解调方式,解码成型需要花费大量的计算时间。而周期特性检测复杂度太高,时间也较长,作为初步实验并不需要如此复杂的检测技术。
本次实验采用能量检测的方法。感知任务如下:
在选取子板所能接收的频率范围内,可以对任意的频段进行能量检测,比如针对RFX400 子板,它的接收范围是 400M-500MHz,可以在 400M-500M 内选定任意范围进行检测,对所检测频段使用情况,能在可控制的时间内记录到文件中,并可通过图形显示出来。
4.2 能量检测 FFT 方法
FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用 FFT 变换的原因。另外,FFT 可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。得到了信号的频域变换后,就可以对其进行模值运算得出某频率值下的幅度特性。
一个模拟信号,经过 ADC 采样之后,就变成了数字信号。采样得到的数字信号,就可以做 FFT 变换了。N 个采样点,经过 FFT 之后,就可以得到 N 个点的 FFT 结果。为了方便进行 FFT 运算,通常 N 取 2 的整数次方。假设采样频率为 Fs,信号频率 F,采样点数为 N。那么 FFT 之后结果就是一个为 N 点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为 A,那么 FFT 的结果的每个点(除了第一个点直流分量之外)的模值就是 A 的 N/2 倍。而第一个点就是直流分量,它的模值就是直流分量的 N 倍。而每个点的相位,就是在该频率下的信号的相位。第一个点表示直流分量(即 0Hz),而最后一个点 N 的再下一个点(实际上这个点是不存在的,这里是假设的第 N+1 个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率 Fs,这中间被N-1 个点平均分成 N 等份,每个点的频率依次增加。例如某点 n 所表示的频率为:Fn=(n-1)*Fs/N。由上面的公式可以看出,Fn 所能分辨到频率为为 Fs/N,如果采样频率Fs 为 1024Hz,采样点数为 1024 点,则可以分辨到 1Hz。1024Hz 的采样率采样 1024 点,刚好是 1 秒,也就是说,采样 1 秒时间的信号并做 FFT,则结果可以分析到 1Hz,如果采样 2 秒时间的信号并做 FFT,则结果可以分析到 0.5Hz。如果要提高频率分辨力,则必须增加采样点数,也即采样时间。频率分辨率和采样时间是倒数关系。
假设 FFT 之后某点 n 用复数 a+bi 表示,那么这个复数的模就是
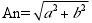 ,相位就是 Pn=atan2(b,a)。根据以上的结果,就可以计算出 n 点(n≠1,且 n<=N/2)对应的信号的表达式为:An/(N/2)*cos(2*pi*Fn+Pn),即 2*An/N*cos(2*pi*Fn+Pn)。对于 n=1 点的信号,是直流分量,幅度即为 A1/N。
,相位就是 Pn=atan2(b,a)。根据以上的结果,就可以计算出 n 点(n≠1,且 n<=N/2)对应的信号的表达式为:An/(N/2)*cos(2*pi*Fn+Pn),即 2*An/N*cos(2*pi*Fn+Pn)。对于 n=1 点的信号,是直流分量,幅度即为 A1/N。
由于 FFT 结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果,即可以是前向 FFT 也可以是后向 FFT,前向、后向各一半结果。
由此可知:假设采样频率为 Fs,采样点数为 N,做FFT 之后,某一点 n(n 从 1 开始)表示的频率为:Fn=(n-1)*Fs/N;该点的模值除以 N/2 就是对应该频率下的信号的幅度(对于直流信号是除以 N);该点的相位即是对应该频率下的信号的相位。相位的计算可用函数 atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值,范围从-pi 到 pi。要精确到 xHz,则需要采样长度为 1/x 秒的信号,并做 FFT。要提高频率分辨率,就需要增加采样点数,这在一些实际的应用中是不现实的,需要在较短的时间内完成分析。解决这个问题的方法有频率细分法,比较简单的方法是采样比较短时间的信号,然后在后面补充一定数量的 0,使其长度达到需要的点数,再做 FFT,这在一定程度上能够提高频率分辨力。
1.1 认知无线电频谱感知原理
目前,在认知无线电领域用于检测某频段内是否有信号存在、有哪些信号存在的方法有多种。以检测类型划分,可分为信号存在性检测和信号覆盖范围检测两类;以检测节点个数划分,可分为单节点检测和多节点联合检测;以检测方法划分,主要分为匹配滤波、能量检测、周期特性检测三类[23]。总结归纳各种方法如图所示:

信号存在检测,是指在经过对某特定频段内信号的进行观测之后,做出该频段上是否有信号存在的判断,这种探测原理的基本模型可以用下面的公式表示:
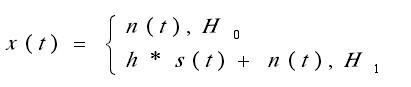
其中,x(t)是认知无线电接收到的信号,s(t)是第一用户传输的信号;n(t)是加性白高斯噪声;h 是信道的增益;Ho 是未被占用的假设,表明了目前在这一确定频段上没有第一用户;H1 是另一种假设,表明目前存在第一用户。
下面将对单节点检测的几种方法进行介绍、分析:
(1)匹配滤波器探测
当认知无线电获悉了第一用户的信号后,静态高斯噪声理想探测器就是匹配滤波器,原因在于它能使接收到的信号的信噪比(SNR)最大化。匹配滤波器的主要优点是它只需很短的时间就可以获得高处理增益。然而,它必须有效地对第一用户的信号进行解调,这就意味着它需要第一用户的先验知识,比如解调方式和阶数、数据包格式等。
上述信息可以预存在认知无线电的内存中,然而,对解调来讲,认知无线电必须通过时间和载频同步甚至信道同步来获得第一用户的相关性。如果这些信息是不准确的,那么,匹配滤波器的性能就会变得很差。匹配滤波器探测的一个明显缺点在于,认知无线电对每一类型的第一用户都要有一个专门的接收器。
(2)能量探测
如果接收机不能够收集到第一用户信号的足够的信息,此时的最佳探测器就是能量探测器。为了测量接收信号的能量,需要对带宽为 W 的带通滤波器的输出信号进行平方运算并在观测时间段 T 内进行积分,并将积分器的输出 Y 与门限值进行比较,从而判定合法用户是否出现。检测过程示意图如下所示:

能量探测器的门限很容易受到噪声功率的变化的影响。为了解决这个问题,已经有文献提出通过第一用户发射机的导频音(Pilot Tone)来提高认知无线电能量探测器的准确性。另外,即使能够适应性的设定门限值,带内干扰的出现也会扰乱能量探测器。能量探测器的另外一个缺点是它只能探测到有用信号出现,而不能够区分信号的类型,即它不能区分已调制信号 、噪声及干扰。因此,能量探测器容易被不明信号误导而产生误判决。
(3)静态循环特征探测
调制信号一般都经过了载波、脉冲序列、重复性扩展、跳频及循环前缀等耦合处理,使已调信号具有了内在的周期性。虽然数据是静态随机的,但是这些调制后的信号的均值和自相关函数都具有周期性,因而称其具有循环性。通过分析频谱自相关函数可以探测出这些特征。频谱自相关函数的最主要的优点是它能够把噪声能量和已调信号的能量区分开来,这是因为噪声是一个宽带的、静态的、没有相关性的信号,而已调信号具有频谱相关性和周期性。静态循环特征探测器具有更强的抵抗噪声功率中不确定性的能力,因而能够比能量探测器更好地分辨出噪声信号。不过,它就比能量探测器更加复杂并且需要更长的观测时间。
4.1.2 感知任务
综合比较上述三种检测方法的优缺点,我们可以得到下面的对比:

在本认知无线电实验平台中,我们选择能量检测的方式做频谱感知。因为匹配滤波需要授权用户的信号模型,只能针对某种信号进行检测,而能量检测的方法对任意信号都适用。而且匹配滤波需要重构到某种调制解调方式,解码成型需要花费大量的计算时间。而周期特性检测复杂度太高,时间也较长,作为初步实验并不需要如此复杂的检测技术。
本次实验采用能量检测的方法。感知任务如下:
在选取子板所能接收的频率范围内,可以对任意的频段进行能量检测,比如针对RFX400 子板,它的接收范围是 400M-500MHz,可以在 400M-500M 内选定任意范围进行检测,对所检测频段使用情况,能在可控制的时间内记录到文件中,并可通过图形显示出来。
4.2 能量检测 FFT 方法
FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用 FFT 变换的原因。另外,FFT 可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。得到了信号的频域变换后,就可以对其进行模值运算得出某频率值下的幅度特性。
一个模拟信号,经过 ADC 采样之后,就变成了数字信号。采样得到的数字信号,就可以做 FFT 变换了。N 个采样点,经过 FFT 之后,就可以得到 N 个点的 FFT 结果。为了方便进行 FFT 运算,通常 N 取 2 的整数次方。假设采样频率为 Fs,信号频率 F,采样点数为 N。那么 FFT 之后结果就是一个为 N 点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为 A,那么 FFT 的结果的每个点(除了第一个点直流分量之外)的模值就是 A 的 N/2 倍。而第一个点就是直流分量,它的模值就是直流分量的 N 倍。而每个点的相位,就是在该频率下的信号的相位。第一个点表示直流分量(即 0Hz),而最后一个点 N 的再下一个点(实际上这个点是不存在的,这里是假设的第 N+1 个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率 Fs,这中间被N-1 个点平均分成 N 等份,每个点的频率依次增加。例如某点 n 所表示的频率为:Fn=(n-1)*Fs/N。由上面的公式可以看出,Fn 所能分辨到频率为为 Fs/N,如果采样频率Fs 为 1024Hz,采样点数为 1024 点,则可以分辨到 1Hz。1024Hz 的采样率采样 1024 点,刚好是 1 秒,也就是说,采样 1 秒时间的信号并做 FFT,则结果可以分析到 1Hz,如果采样 2 秒时间的信号并做 FFT,则结果可以分析到 0.5Hz。如果要提高频率分辨力,则必须增加采样点数,也即采样时间。频率分辨率和采样时间是倒数关系。
假设 FFT 之后某点 n 用复数 a+bi 表示,那么这个复数的模就是
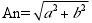 ,相位就是 Pn=atan2(b,a)。根据以上的结果,就可以计算出 n 点(n≠1,且 n<=N/2)对应的信号的表达式为:An/(N/2)*cos(2*pi*Fn+Pn),即 2*An/N*cos(2*pi*Fn+Pn)。对于 n=1 点的信号,是直流分量,幅度即为 A1/N。
,相位就是 Pn=atan2(b,a)。根据以上的结果,就可以计算出 n 点(n≠1,且 n<=N/2)对应的信号的表达式为:An/(N/2)*cos(2*pi*Fn+Pn),即 2*An/N*cos(2*pi*Fn+Pn)。对于 n=1 点的信号,是直流分量,幅度即为 A1/N。由于 FFT 结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果,即可以是前向 FFT 也可以是后向 FFT,前向、后向各一半结果。
由此可知:假设采样频率为 Fs,采样点数为 N,做FFT 之后,某一点 n(n 从 1 开始)表示的频率为:Fn=(n-1)*Fs/N;该点的模值除以 N/2 就是对应该频率下的信号的幅度(对于直流信号是除以 N);该点的相位即是对应该频率下的信号的相位。相位的计算可用函数 atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值,范围从-pi 到 pi。要精确到 xHz,则需要采样长度为 1/x 秒的信号,并做 FFT。要提高频率分辨率,就需要增加采样点数,这在一些实际的应用中是不现实的,需要在较短的时间内完成分析。解决这个问题的方法有频率细分法,比较简单的方法是采样比较短时间的信号,然后在后面补充一定数量的 0,使其长度达到需要的点数,再做 FFT,这在一定程度上能够提高频率分辨力。
- 基于GNU Radio和USRP的认知无线电平台研究(11-07)
- 认知无线电中频谱感知技术的研究进展(11-11)
- 认知无线电在军事中的应用(11-11)
- 认知无线电的频谱占用度研究(01-02)
