频谱分析基本原理：快速完成高效率测量

依据选定的频距、RBW和VBW，来自动选择所允许的最快扫描时间。此外，不同的频谱分析仪，其扫描速度也各不相同。

　　˙灵敏度

　　接收器的灵敏度代表仪器在某些测试环境下能够接收微小讯号的能力。所有接收器（包括频谱分析仪）多多少少都会有一些内部产生的杂讯，而频谱分析仪的灵敏度以RBW设为最低时之显示平均杂讯位準（DANL）来表示，单位为dBm。

　　DANL亦即仪器在特定频宽下的杂讯位準。如果输入讯号低于杂讯位準时，我们就无法用频谱分析仪量这个微小讯号。一般而言，频谱分析仪的灵敏度约在-135 dBm到-165 dBm之间。如欲获得最佳灵敏度，请将RBW设为最低、充分进行平均处理、将射频输入衰减设到最小，并且使用前置放大器。不过提高频谱分析仪的灵敏度，可能会与降到失真或是增加动态範围等其他量测需求相衝突。

　　˙失真

　　叁阶交互调变与谐波失真等失真量测是惯用的元件特性分析方法，但需注意频谱分析仪本身也会产生失真，因而导致量测误差。如果频谱分析仪内部失真的程度与DUT之外部失真不相上下，量测误差便会增加。在最糟状况下，内部失真可能会完全盖过DUT的失真。仪器製造商可直接设定频谱分析仪的失真程度，或是与动态範围规格整併在一起。

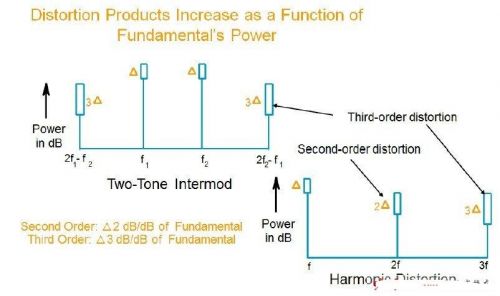
图叁 二阶失真会以基础讯号增量的平方增加，而叁阶失真则以立方增加。

叁阶截断点（TOI）是评量频谱分析仪是否能够处理大讯号而且不会失真的指标。TOI较高的分析仪，通常可以提供绝佳动态範围与準确度，以便量测失真与杂讯

　　在进行量测之前，使用者须先确认分析仪产生的失真是否会影响量测结果。例如，在执行双音调测试时，指定仪器的失真产物（叁阶失真）大于50 dB，而二阶失真（谐波失真）大于40 dB。这些数值可作为分析仪必备的最低规格。为减少内部失真所导致的量测误差，内部失真必须比测试规格小很多。

　　图叁显示非线性元件的失真。为了确认失真到底是由分析仪内部所产生，亦或是DUT所导致，我们需进行衰减测试。首先将射频输入讯号衰减10dB，如果萤幕中失真产物的大小没变，那就可确定是DUT所产生的失真。但如果萤幕显示的讯号大小改变了，那么失真可能有一部分是讯号分析仪内部所产生的，而非完全是DUT所致。

动态范围

　　频谱分析仪的动态範围是指在一次量测中可测得的最大与最小讯号的差值，因而可量测到更小的不确定性，如图四所示。动态範围的单位为dB。分析仪的动态範围是指可以可靠地执行讯号量测的範围。动态範围经常被误解与误判，因为仪器的显示範围、量测範围、杂讯位準、相位杂讯，以及突波响应，都对于动态範围影响甚鉅，如图五所示。

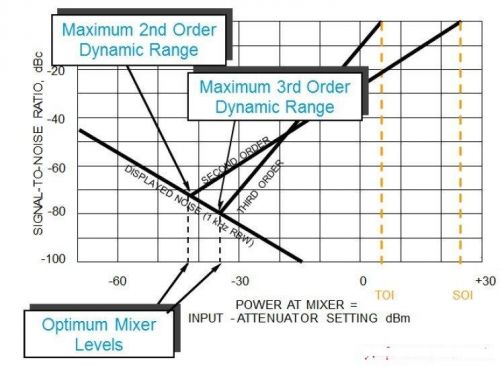
　图四 您可用图形方式呈现动态範围。

本图显示在同一动态範围图中的讯号对杂讯（signal-to-noise）和讯号对失真（signal-to-distortion）曲线。当不同曲线相交时，亦即内部产生的失真位準等于显示平均杂讯位準（DANL），则动态範围最大。这一点同时也是最大混频器位準。

　　为了获得最佳的动态範围，请选择具备最佳灵敏度的分析仪，亦即具有最窄RBW、最小输入衰减，并彻底执行平均处理的机型。请持续衰减输入讯号并查看讯号大小是否改变，以确认分析仪的失真情形。接着，请在不改变讯号大小的状况下将衰减器设为最低。

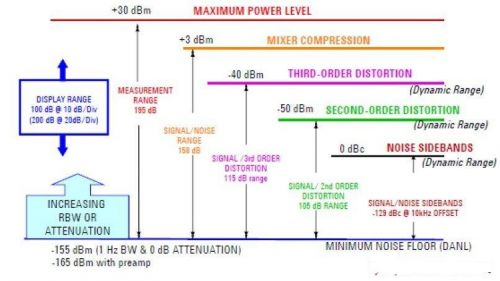
图五 图中显示各个动态範围的定义，

　　藉此工程师可得知道哪一种动态範围最适合哪一个特定应用

现代讯号分析仪

　　传统的频谱分析仪无法因应现代数位调变无线系统的测试需求，而新型分析仪的问市，则满足了

　　这类系统的通道功率测试、解调变量测等新型态测试需求。此外，新式频谱分析仪拥有齐备的功

　　能，可支援更广泛的标準与特性，例如出色的振幅準确度、频距和频率準确度、修正係数，以及

　　限制线（limit line）、测试余裕，及通过/不通过指示等等，因此可有效执行前述测试。有些机型甚至

　　提供即时讯号撷取功能，以便在一段时间内，撷取与某一讯号相关之所有资讯。

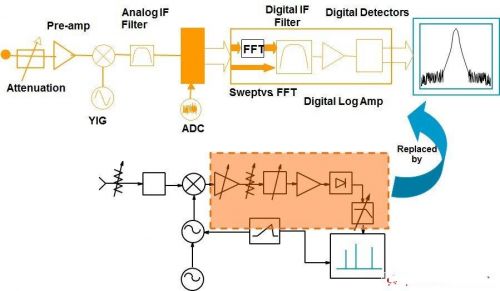
图六 现代频谱分析仪之基本架构方块图，本图为Agilent X 系列讯号分析仪之方块图

　　相较于传统的频谱分析仪，新型分析仪配备各种不同的元件，并且重新安排了功能模组，并且将ADC的位置移到处理流程的前端，如图六所示。新型分析仪的全数位化IF滤波器可用崭新方式处理讯号，进而大幅提昇準确度、动态範围及速度。

　　其内建的数位讯号处理器（DSP）让分析仪能够量测日益复杂的讯号，同时也进一步增加动态範围与準确度，并且加快扫描速度。在需要更大动态範围时，可透过扫描分析模式处理讯号，但如需在窄小频宽中快速进行扫描的话，则可使用FFT分析模式处理讯号。

更重要的是，新型频谱分析仪提供内