转子振动信号的盲源分离研究

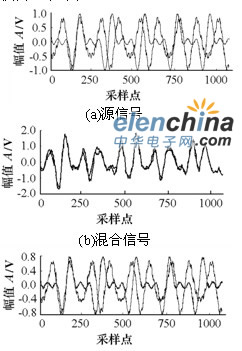
　　　　　　　　　　　　　　　　　　　　　图4 两个谐波信号的分离

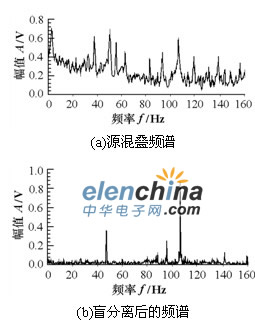
　　　　　　　　　　　　　　　　　　　　图5 实际振动信号的盲分离

4.3 基于峭度的快速定点算法

　　经典的测量非高斯方法是峭度(kurtosis)或称四阶累积量。有关研究用基于峭度的快速定点算法对真实的转子振动信号进行了盲源分离研究。在转子振动试验台上安装4个加速度传感器，三个加速度传感器是安装在轴承座上的，另一个安装在垂直于转子轴的连接盘上以便测量轴向的振动情况。试验时的转速为525转/分。由此得到4个采集信号。

　　值得注意的是，实际采集的信号一般就是混合后的信号。所以前述数值仿真分析方法中，"信号混合"这一步就不需要了，可以在直接对采集的信号进行预白化处理后，再用基于峭度的快速定点抽取算法进行分离。

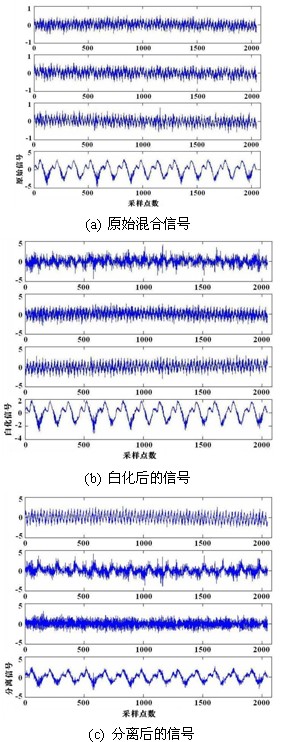
　　　　　　　　　　　　　　　　　　　　图6 转子振动信号的盲源分离

　　由传感器测得的4个振动源信号如图6(a)所示；预白化处理后的信号、分离后的信号分别如图6(b)、(c)所示。从图6(a)可看出，从原始的转子振动信号中只能分辨出轴向冲击信号，而其他3个信号波形十分相近，无法识别出哪个信号是哪个振动源产生的。从图6(c)中能够清晰地分离出不同的振动信号源。第四个信号是明显的轴向冲击信号，第二个信号是转子旋转的信号，第一个信号是轴承滚子的冲击信号，第三个信号是噪声信号。这说明用基于峭度的快速定点算法对转子振动信号的盲源分离是十分有效和成功的。

4.4 改进的基于Jacobi优化的极大似然估计方法

　　在传统的Jacobi优化算法的基础上，文献[10]探索了一种具有初始化四阶矩矩阵的优化算法，来提高算法的收敛速度和计算效率。

　　用6个模拟源信号进行混合，分别用FastICA算法、JADE算法来与改进Jacobi优化算法进行比较，采取采样点数从5000变化到30000，来依次统计各个算法的计算时间。3种算法的计算效率如图7所示。可以看出JADE算法的计算时间相比于其它两个算法要长，这在大采样点情况下表现更为明显，而基于初始化四阶矩矩阵的算法与FastICA算法有着接近的计算时间(相差3%左右)

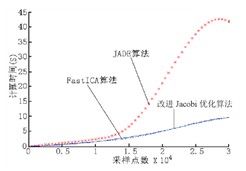
　　　　　　　　　　　　　　　　　　　　　图7 三种算法的计算效率

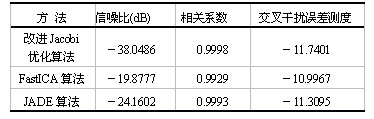
　　利用仿真试验来分析各个算法分离信号的信噪比、相关系数以及交叉干扰误差测度，如表1所示。这三个指标的值越大表明算法实现的分离信号就越逼近源信号，分离的性能就越优良。从表1可以看出，该算法可以得到优于其它两个算法的信噪比、相关系数以及交叉干扰误差测度。所提出的算法在分离信号的性能指标上远优于FastICA算法。

4.5 鲁棒的二阶非平稳源分离方法

　　D. T.Pham对于一组对称正定矩阵{Mi}提出了一个不同的准则，它不需要进行任何预白化，而且对角化矩阵同时也是分离矩阵[30]。对于有不同功率谱(或等价于不同的自相关函数)的有色源，可以使用时滞协方差矩阵，并由此得到了二阶盲辨识(SOBI)算法。Choi和Cichocki对非平衡源SOBI进行修改，提出一种高效灵活的二阶非平稳源分离(SONS)方法 [31]。

　　　　　　　　　　　　　　表1 各个算法分离信号的性能指标

用与4.3节相同的实验台，用SONS算法对噪声含量较少的转子系统中低转速数据进行分离，与基于负熵的快速定点算法相比，SONS算法在分离效果上的改善很小。在含有大量噪声的高速旋转情况下，基于负熵的快速定点算法对转子振动信号的分离结果如图8(a)，在改用SOBI算法后，分离结果得到了改善，如图8(b)。而在改用SONS算法，分离结果的改善则很明显，如图8(c) [32]

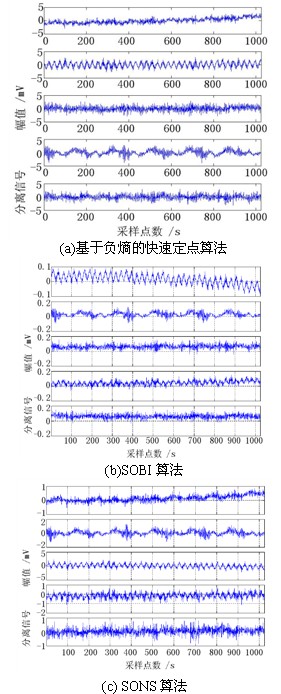
　　　　　　　　　　　　　　　　　　　图8 用三种算法对高速数据盲源分离结果的比较
5 结论

　　本文介绍的内容为将盲源信号分离技术应用于机械振动信号的故障诊断提供了一个依据，也为盲源信号分离应用于实际工程信号的处理打下了基础。

　　今后应该着重研究的发展方向主要有3个：
　　(1) 如何实现在观测量个数源信号个数不确定或未知时的盲分离方法研究。
　　(2)更一般的非线性混叠的可分离性的研究。
　　(3)对含有噪声的混叠信号进行盲分离方法的研究。