一种新的基于时域方法的EMC测试技术

本文讨论了宽带时域测量技术应用于测量电磁干扰(EMI) 时所具备的优势。宽带时域测量技术用于EMI测量时，其数字信号处理能力使它能够实时仿真传统模拟设备的各种测量模式，如峰值检测模式、平均值检测模式、 RMS检测模式和类峰值检测模式。同时，它还能引入诸如相位谱、短时谱、统计评估以及基于FFT的时－频分析方法等新的分析理念。由于时域技术允许对整个 信号谱内的幅度和相位信息进行并行处理，因此测量时间至少可以缩短一个数量级。本文还讨论了该技术中用到的信号处理算法和利用时域电磁干扰系统(TDEMI)进行实际测量得到的测量结果。

随着新技术的飞速发展，新的电子产品层出不穷。如何使电子产品满足电磁兼容要求，并改善其电磁兼容性能，这已经成为产品开发 过程中的一大难题。EMC和EMI测量设备能够在较短的测量时间内提取大量精确的信息，采用这种设备能够降低产品开发成本，并提高电路和系统开发的质量。 一直以来，人们都是使用超外差射频接收机[1][2]来测量射频噪声和电磁干扰(EMI)。这种方法的缺点是测量时间过长，对于30 MHz到1 GHz频带内的电磁干扰，通常需要测量30分钟。测量时间过长就导致测试成本高昂，因此必须寻求一种能够在不损失测量质量的前提下缩短测量时间的方法。传 统的测量系统并不评估被测EMI信号的相位信息，从而导致重要信息被丢失。而采用了傅立叶变换的EMI测量技术，其数字化处理就允许将时域内测量得到的信 号分解成各种频率成分。近几年，随着快速傅立叶变换(FFT)程序带来的经济效益日益明显，FFT技术的应用已经快速普及起来。

本文讨论了几种新的信号处理方法，采用这几种方法，时域测量技术能够完成精确高效的EMI测量。此外，本文还介绍了为准确测量各种EMI信号而采用的信号处理策略。

时域电磁干扰测量系统

图1所示为一个时域测量装置的框图，其中包含一个时域电磁干扰(TDEMI)测量系统和一个用于与TDEMI做比较的传统 EMI接收机。TDEMI系统中包含：宽带天线(HL562, Rohde&Schwarz)、线性阻抗稳定网络(ESH 2-Z5, Rohde&Schwarz)、开关单元(RSU, Rohde&Schwarz)、放大器(ZFL-1000LN, Mini-Circuits)、低通滤波器(SLP-1000, Mini-Circuits)、模数转换器(TDS7154, Tektronix, 示波器)和一台个人计算机(兼容IBM)。文献[3]中已经讨论了TDEMI测量系统的硬件，该系统的工作基础是对采样后的EMI信号进行数字处理，其优 点之一就是能够通过软件方式改善系统性能。

信号处理理论

ADC以采样频率fs 对输入连续信号进行采样和量化，相应的采样间隔为1/fs = ?t。根据香农定理，fs至少应为信号最高频率的两倍。这一由采样频率决定的信号频率上限也叫做奈奎斯特频率。数字化之后，数据按N个样本块的形式送入估 值程序，作为谱估计器的输入。TDEMI系统中所采用的谱估计方法的数学基础就是离散傅立叶变换(DFT)。对每一个数据块进行的DFT变换定义如下：

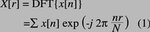
DFT将离散时间信号序列x[n]变换为离散频谱序列X[r]，其中n和r表示离散时间变量和离散频率变量，并且n和r均为0到(N－1)之间的整数：

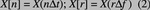
根据DFT的基本特性，?f 、N和 ?t之间满足如下关系：

在频谱X中，X[0]反映了信号的直流均值，而绝对值 则对应于在频率标记为r处的合成矢量的幅度。要计算RMS值，必须将 中每个r > 1的元素均除以正弦信号的振幅因数 。而对应于奈奎斯特频率的频率标记R见下式：

由于一个实值信号经DFT变换后的绝对值是r的奇函数，因此信号的所有谱信息均包含在大于或小于奈奎斯特频率的半边X[r] 中。于是，后面的估值步骤只需要X[r]的一半就足够了。信号能量在两半频谱中平均分布，因此必须将 的 值乘以2才能准确地用单边带形式表示整个频谱。要获得与连续傅立叶变换类似的结果，DFT得到的谱值还必须进一步对时域样本数N归一化处理。下式定义了单 边幅度谱：

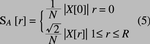
在实际的系统中，式(1)是通过快速傅立叶变换(FFT)实现的。为了避免当信号中包含非信号周期整数倍的周期成分时，频谱泄漏至观测时间 内，应该加上一个窗函数。

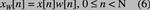
窗函数在N/2处达到全局最大值，并向两边平滑滚降，在0和N-1处达到0，这样就消除了对x[n]加窗时的边沿效应。另一 方面，加窗后的信号向量xW[n]所携带的能量比原始信号少，因为部分信号被削弱了。为了消除这一影响，我们限制窗函数序列，使其在观测时间?TN内的积 分等于1。w[n]的换算系数被称作相关增益GC：

GC是一个换算系数，所以根据DFT的线性特性，GC可以与其他换算系数一起在频域中进行谱变换之后使用。这样，我们就得到了以下