测量周期抖动有助于描述时钟的短期和长期稳定性

周期抖动可以描述为在一段不相邻脉冲时间内发生的定时变化。测量周期抖动有助于描述时钟的短期和长期稳定性。

精确度

进行参数测量前，需要知道对测量精确度的要求，以保证测量时留出足够的测量公差和测试裕量，抖动测量也不例外。泰克通过以下 几个因素来定义仪器的抖动测量能力：仪器的基本定时和幅度精确度、仪器的基本噪声基底以及内插误差。内插误差应小于0.3ps RMS(在测量tr为100ps的信号，并且以50%为检测门限时)。

这一误差可以更小，在许多情况下，采用SIN(X)/X内插可以使其得到改善。仪器的基本噪声基底是由ADC的合成误差造 成的，其中包括幅度噪声和定时误差。在TDS7404上这一噪声基底通常小于1.5ps，在TDS6604上通常小于0.7ps。这一测量结果是通过 TIE法，即比较被测的测试信号(来自一台BERT或者其他超稳定时钟源)与一个恢复后的时钟，而得到的。

仪器的基本精确度是抖动测量精确度的灵魂所在，这是可追踪的测量。泰克这样定义时间的变化精确度(Delta Time Accuracy)：对于任何使用示波器进行的测量，绝对定时误差都不能大于一个给定值。这一定义通常可以用一个等式表示，等式中包含几个参数，例如采样率、测量时间以及示波器前端。下文中将更详细地介绍测量时间变化的精确度(Delta Time Accuracy)。

分辨率

测量分辨率是指仪器可检测到的最小的变化。它与测量精确度和可重复性不同。系统对被测信号中所发生的改变的分辨能力受许多因 素限制。对于定时测量而言，分辨率就是指系统分辨信号定时中所发生的微小改变的能力，至于这种改变是有意的改变还是无意的则无关紧要。限制定时分辨率的因 素可以是硬件快速计数能力这种实质上的因素，也可以是软件平均计数能力这种模糊的因素。

在典型的时间间隔分析仪(Time Interval Analyzer，TIA)这样的硬件定时器中，定时分辨率受硬件限制，只能到几百千万亿分之一秒(飞秒，femtosecond)，也就是说，这样的硬件无法检测出任何小于0.2ps的定时变化。

在实时示波器中，分辨率则受采样率、内插精度和基于软件的数学库的限制。如果采用20GS/s的采样率，并采用SIN(X)/X内插，那么 分辨率可能达到几十个飞秒。这时，系统分辨率由数学库决定，因此实际的分辨能力可达亚千万亿分之一秒(sub-femto-seconds， 0.0001ps)级，但这种分辨率是无用分辨率。

从统计的观点上来说，分辨率表示了系统测量变化的能力，但还要考虑系统的整体噪声基底。即还要考虑检测到的变化是由信号造成的还是由系统噪声造成的。要理解分辨率或者整体精确度的真正极限，只知道系统分辨率是无济于事的。

抖动噪声基底

什么是抖动噪声基底？本质上说，抖动噪声基底是指当仪器上没有加入被测信号时得到的测量结果，或者叫测量基底。根据定义，抖 动是指一个信号从应发生的时刻到实际发生的时刻之间的定时变化，或指瞬时事件发生的时刻相对于一个预期的或者已知的时刻的测量结果，因此噪声基底是一个 AC参数。对整个系统性能来说，噪声基底对测量分辨率和测量精确度的影响程度是一个非常重要的特性。试想如果一个系统具备10ns的分辨率，而其噪声基底 就有100ns，那么10ns这个分辨率还有什么意义？只有当被测抖动大于100ns的噪声基底时，测量才有效。对抖动噪声来说也是如此。如果被测抖动大 于系统的抖动噪声基底，那么抖动幅度的变化就能被检测到。但如果被测抖动小于抖动噪声基底，那么抖动中的变化就会被完全掩盖掉。

整个系统的精确度也受到系统噪声基底的限制，不可能高于噪声基底。如果系统噪声就有2ps，其精确度就不可能到1ps。

测量时间变化(DTA)的精确度TDS6604的DTA定义为：

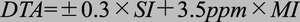
其中，SI为采样间隔，单位为秒；MI为测量间隔，单位也是秒；±0.3则是示波器捕获系统的一个固定常数。

根据这个公式，我们可以得到任何定时测量的测量精度。但这个公式对精度而言真正意味着什么呢？来看两个例子，一个是周期较短的时钟，另一个则较长。首先，我们用TDS6604，以20GS/s的采样率对一个1.0GHz的快时钟进行实时采样。

根据DTA等式，我们可以得到：

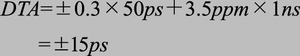
上式给出的是任何一次在单次或实时捕获过程中进行的测量能够得到的峰值测量误差。当样本个数很多时，以1,000次测量为例，该误差的标准差通常等于0.06xSI+3.5ppmxMI。本例中，误差标准差约等于3.0ps RMS。