浅谈嵌入式软件系统设计中的正交性

　　摘要 嵌入式软件系统设计领域存在"正交"的思想。本文结合实际项目经验，总结了软件系统正交化的方法，同时较全面地分析了正交性给嵌入式软件设计带来的诸多方便，最后回顾"正交"思想对不同自然科学领域的积极影响与启发。

　　关键词 嵌入式软件设计 正交性 小波

　　1 小波漫谈

　　小波变换是20世纪最辉煌的科学成就之一，已经广泛应用于信号处理、图像分析、非线性科学、地球科学、音乐雷达、CT成像、地震勘探、天体识别、量子场论、机械故障诊断、分形等科技领域。

　　20世纪初，哈尔(Alfred Haar)对在函数空间中寻找一个与傅里叶类似的基非常感兴趣。1909年他最早发现和使用了小波，后来这被命名为哈尔小波(Haar wavelets)。20世纪 70年代，当时在法国石油公司工作的地球物理学家 Jean Morlet提出了小波变换 WT(Wavelet Transform)的概念。 进入 20世纪 80年代，法国科学家 Y.Meyer和他的同事开始研究系统的小波分析方法。1985年，Daubechies提出"正交小波基"，并构造具有紧支撑的光滑小波，以及随后 Mallat提出的多分辨分析及快速小波变换，将小波研究推向高潮。小波分析己经成为目前发展最快和最引入注目的学科之一，几乎涉及信息领域的所有学科。

　　为何"正交小波基"与多分辨分析的提出成为小波分析发展史中的重大突破成就？主要原因之一是：变换系数没有冗余，能够将信号分解成互不影响的正交子信号，这样就可以根据需求方便地对所需特征的子信号进行分析，从而很好地反映信号的细节。

　　2 嵌入式软件系统设计的正交性

　　其实，在软件系统设计领域同样或多或少存在"正交"的思想。一个常被引用的模式是Smalltalk编程语言（Krasner和 Pope，1988）的模型视图控制器(ModelViewController)框架。该模式强制性地将软件系统的输入、处理和输出分开，形成数据模型、视图、控制器三大模块，如图1所示。图中"数据模型"包括程序的设计部分，"视图"表示用户界面，"控制器"定义用户和视图的交互方式。

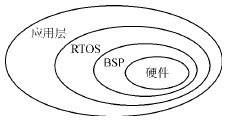
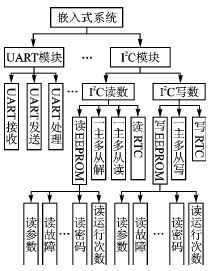
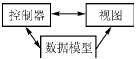图1 模型视图控制器框架 　　其中每部分都是一个独立的对象，每个对象有自己处理数据的规则。这种功能的分离恰巧促成各个模块的正交性、减少它们之间的冗余，因此也使该框架成为应用最为广泛的模式之一。 　　2.1 设计正交嵌入式软件系统 　　毫无疑问，正交的思想使得系统设计更加清晰和方便。那么如何才能更好地使嵌入式软件系统具有"正交性"呢？ 　　（1） 设计具有正交性的系统体系结构 　　进行系统设计首先要进行系统的体系结构设计。系统的宏观设计同样也体现正交性思想，如图2所示。 图2 系统体系结构 　　其中，底层驱动与RTOS是唯一与系统硬件相联系的模块，直接负责与硬件打交道，对硬件进行管理与控制，并为其上层模块提供所需的驱动支持；调度程序在RTOS支持下，根据系统需求对不同的任务模块进行实时调度与管理，确保所有任务能顺利、均衡地执行；最上层的任务模块具有不同的功能，以满足用户需求，它们各自独立、正交、不存在冗余，同时提供相应数据接口，以便与其他模块通信，形成有机整体。 　　整个系统体系结构同样体现了正交思想，各个层的不同模块负责相互独立、正交的任务。从垂直角度看上去，该体系结构同正交小波一样，可以用多尺度空间思想表示，如图3所示。越核心的地方，功能轮廓越粗略；越到外层，越体现细节、越贴近用户需求。 图3 多尺度嵌入式软件体系结构 　　（2） 保持模块间的松耦合 　　划分软件模块时很重要的一个原则是：尽可能地保证各模块间的松耦合和模块内部的高聚合。这实际上就实现了系统的正交化，减少了模块间的冗余与关联。理想的系统结构呈树状，如图4所示。 图4 嵌入式系统的理想树状结构 　　整个系统呈树状结构，模块间的连接只能存在上下级之间的调用关系，不能有同级模块之间的横向关系，即不能出现网状结构或交叉调用关系。 　　如图4所示，通过调用I2C总线读写子模块可以实现I2C一主多从通信子模块以及RTC和EEPROM的读写子模块，但是这些子模块之间彼此不能互相调用。所以，当系统对EEPROM没有需求时，可以方便地将EEPROM读写子模块移除，而不会影响到其他模块。 　　（3） 保持任务间的松耦合 　　嵌入式系统中常常会用到RTOS，根据系统需求确定不同的任务以及任务执行的频率或次序。在满足需求的前提下，尽可能地保证每个任务有固定的执行周期，因为这样可以让任务按照既定频率执行，减少任务间的通信和调用，同时也增强了系统的可预见性。 　　例如，系统SPI通信解析任务（即ProcSPI任务）的执行频率为10 Hz，为了保证通信正常，需要一个任务实时检测SPI通信是否出现故障（即FaultSPI任务）。为说明简便，假设SPI通信故障的唯一来源是数据解析时校验不通过，并且当出错概率超过50%时即可判定SPI通信故障。图5所示为FaultSPI任务被调用的2种方式。 　　图中，MCscheduler为系统调度程序，能以固定频率调用不同的任务。图5（a）表明每次解析SPI数据时，都直接触发FaultSPI 任务。显然，根据需求，该方式做了许多无用的判断。图5（b）表明FaultSPI任务由系统调度程序以1 Hz的频率调用。该任务只需要确定SPI数据有5次以上校验错误，即可判断SPI通信故障。这种方式消除了2个任务的直接调用关系，即保持了任务间的松耦合。 　　（4） 合并同类项 　　以模块或文件为单位，每个模块或文件面向独立的设备或需求，每个模块又由许多子模块构成，这些子模块尽可能负责独立、单一的任务或功能。如 GetTime()、SetTime()、GetFault()、PushFault()等，这些子模块可能会调用相同的函数或方法，也可能会使用同一个属性变量，如果将这些子模块归在一起，封装成一个文件，那么这些被调用的函数、方法或变量就不需要"extern"声明(C语言中)，因此对于其他文件是隐藏的、不可见的，增加了系统的安全性；另外，当不需要该功能或设备时，可以方便地将该文件从项目中移除，而不会影响到其他模块的工作。 　　（5） 避免编写相似函数 　　功能相似的函数往往很难保持正交性，所以应该避免相似函数的出现，或者将其统一成一个函数。比如，一个系统存在着多种通信方式，而在通信过程中，常常需要开发者确定自己的通信协议以及校验方式；如果每一种通信方式都编写自己的校验函数，则增加代码量的同时，也使得系统通信校验函数过于零散；在设计时，可以考虑统一系统中的通信校验方式，编写一个校验函数，以支持各类通信的校验。这样既能使系统简洁，同时也便于维护。 　　2.2 正交嵌入式系统的好处 　　正交思想几乎触及到自然科学的各个领域，利用该思想来进行嵌入式软件系统设计同样存在诸多优点。