手机接收通道噪声系数测试

针对手机等接收机整机噪声系数测试问题，该文章提出两种简单实用的方法，并分别讨论其优缺点，一种方法是用单独频谱仪进行测试，精度较低；另一种方法是借助噪声测试仪的噪声源来测试，利用冷热负载测试噪声系数的原理，能够得到比较精确的测量结果。

问题提出

下图是MAXIM 公司TD-SCDMA 手机射频单元参考设计的接收电路，该通道电压增益大于100dB，与基带单元接口为模拟I/Q 信号，我们需要测量该通道的噪声系数。我们现有的噪声测试仪表是HP8970B，该仪表所能测量的最低频率为10MHz，而TD-SCDMA基带I/Q 信号最高有用频率成份为640KHz，显然该仪表不能满足我们的测量需求。

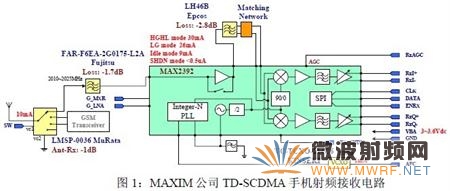
下面我们将介绍两种测试方案，并讨论其测试精度，最后给出实际测试数据以做对比。

利用频谱仪直接测试

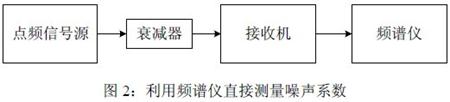
利用频谱仪直接测量噪声系数的仪器连接如图2 所示，其中点频信号源用于整个通道增益的校准，衰减器有两个作用，一是起到改善前端匹配的作用；二是做通道增益校准使用，因接收机增益往往很高，大于100dB，而一些信号源不能输出非常弱的信号，配合该衰减器即能完成该功能。

测量步骤一，先利用信号源产生一个点频信号（一般我们感兴趣的是接收机小信号时的噪声系数，故此时点频信号电平应接近灵敏度电平），频点与本振信号错开一点，这样在基带I/Q 端口可以得到一个点频信号，调节接收机通道增益使I/Q 端点频信号幅度适中，测量接收机输入与输出端的点频信号大小可以求得这时的通道增益，记为G；

测量步骤二，接步骤一，关闭信号源，保持接收机所有设置不变，用频谱仪测量I/Q端口在刚才点频频点处的噪声功率谱密度，I 端口记为Pncdensity(dBm/Hz), Q 端口记为Pnsdensity(dBm/Hz)，则接收通道噪声系数有下式给出：

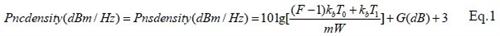
上式中kb 表示波尔兹曼常数，F 是噪声系数真值，我们用NF 表示噪声系数的对数值，NF＝10lg(F)， G 表示整个通道增益，T1 为当前热力学温度，T0 等于290K。假定T1＝T0，容易求得NF 的显式表达式如下：

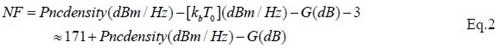
或者：

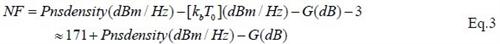
关于方程2 与方程3 的正确性，我们可以做如下简单推导。先考虑点频情况，设接收机输入端点频信号为：

接收机I/Q 端口点频信号分别为：

现在考虑噪声问题，为简化计算，这儿设当前温度为290K，即定义噪声系数的标准温度。根据噪声系数的定义，我们可以将系统产生的噪声等效到输入端口，该噪声与资用噪声功率和应等于资用噪声功率的F 倍。下面我们用一个窄带平稳高斯过程来描述这两部分噪声之和，设噪声带宽为2B，下面方程给出了该噪声的一些特性：

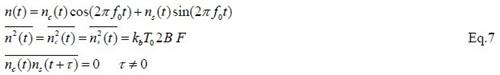
比较方程4 与方程7，再参照方程5 式与6 式，我们可以得到接收机输出端的噪声表达式：

结合方程8 与方程7 可以直接得到方程2，结合方程9 与方程7 可以直接得到方程3，注意I 与Q 端口噪声带宽为B，是射频噪声带宽的一半。下图比较形象地给出了噪声变换过程:

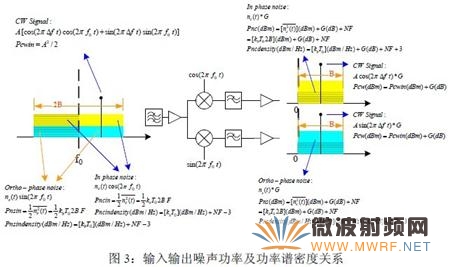
从上图还可以看到，在数值上，输出同相噪声功率谱密度与输入同相噪声谱密度除通道增益与噪声系数外，相差6dB，这说明输入同相噪声上下两边带是严格相关的；输出正交噪声谱密度与输入正交相噪声谱密度相比除通道增益与噪声系数外，同样也有6dB 增益。

借助标准噪声源精确测试

这里介绍的方法即Y 系数法，也称为冷热负载法，一般噪声系数测试仪表就采用该方法，但仪表有它自身的限制，如HP8970B 所能测量的最低频率为10MHz，待测件最大增益80dB。我们这里采用通用频谱仪来检测待测件输出噪声大小，从而避开了噪声测试仪表在噪声检测上的限制，再根据Y 系数法原理计算出待测件噪声系数。下图给出了该方法的仪器配置图：

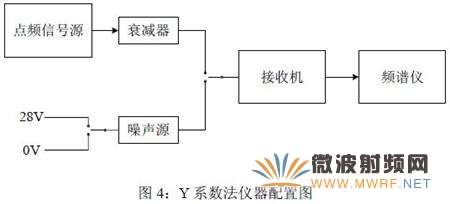
测量步骤一，先将接收机接到点频信号源侧，利用信号源产生一个灵敏度电平的点频信号（因为我们通常感兴趣的是接收机小信号时的噪声系数），频点与本振信号错开一点，这样在基带I/Q 端口可以得到一个点频信号。调节接收机通道增益使I/Q 端点频信号幅度适中；

测量步骤二，接步骤一，保持接收机所有设置不变，将接收机接到噪声源一侧，噪声源置为冷态，设冷态噪声温度为T1，用频谱仪测量I 端口噪声功率谱密度（I 与Q 有相同的性质，故此处仅提及I 端口），记为Poc(dBm/Hz)；

测量步骤三，接步骤二，保持接收机设置不变，噪声源置为热态，设噪声温度为T2，用频谱仪测量I 端口噪声功率谱密度，记为Poh(dBm/Hz)；所谓 Y 系数法中的Y 即测量步骤三与测量步骤二两测量值的比值：

设接收机等效噪声温度为Te。我们可以用冷态源噪声温度，热态源噪声温度，接收机等效噪声温度来表示系数Y，如下式：

设噪声头超噪比为ENR，标准噪声温度为T0（290K），根据超噪比定义可得到下面等式：

根