利用对数放大器和MCU增强RF功率测量精度

到的检测器电压，很容易计算现场的发射功率。利用两点校准的重要优点就是减少成本、缩短测试时间。然而，这种校准方法仅是由于对数放大器的线性性能才成为可能。

因为校准通常是在一个温度下做的，所以温度对检测器的定量影响是很非常重要的。对数检测器的精度随温度的变化可用一致性误差表示。图4示出工作频率高达3.5 GHz的45 dB对数放大器在900 MHz的传递函数。图中包括在-40ºC和+85ºC时的传递函数，以及对数一致性误差随温度变化的关系曲线。因为所谓的两点校准情况，用相同的25ºC线性参考产生三条线性一致性误差曲线。

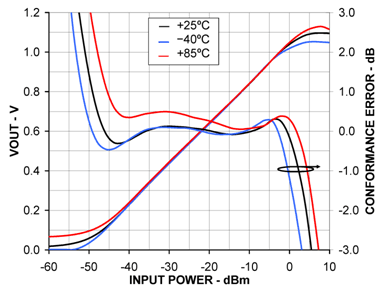
图4. 在900 MHz处单个器件的对数一致性误差示出工作温度范围内±0.5dB的精度。

对数放大器在25°C环境温度的传递函数具有50.25 dB/V的斜率和-51.6 dBm的截距（线性参考直线的延长线与X轴的交点）。25°C的曲线在0 dB误差线周围波动，然而，在两端温度处具有较小的斜率和截距偏移。在工作温度范围和40 dB检测范围内，单个器件的对数一致性误差保持在±0.5 dB以内。在+85°C时的温度漂移是动态范围的限制。虽然单个器件在工作温度范围内可能会有好的精确度，然而由于半导体制造工艺引起的器件之间固有的细小差异可以证明对于精确的RF功率管理是一种障碍。

图5示出70个器件对数一致性误差的分布。在很宽的器件范围内抽样以证明制造工艺引起的偏差。每个器件都有三条相对25°C线性参考值校准的温度曲线。尽管器件与器件之间有明显的偏差，但其分布值非常接近。在工作温度范围和大于40 dB的检测范围内器件的总体分布曲线具有±1 dB的精度。由于器件与器件之间具有可重复性的漂移从而引入温度补偿。

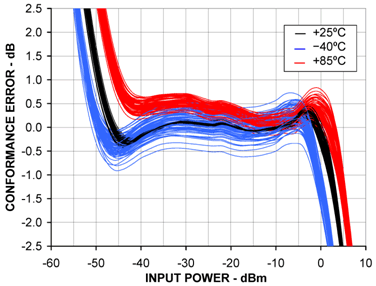
图5. 器件之间的对数一致性误差明显不同，但其总体分布非常接近。

通常无线通信标准要求发射功率检测方案具有±1-dB 和±2-dB的精度，而在极端温度则放宽限制。对数放大器的初始精度无需精细调整便足够满足大多数标准。尽管如此，对数放大器还是有很多明显优点，它们超出了由不同标准决定的RF功率管理要求。

MCU如何能补偿误差

正如前面所讨论的，MCU能够利用发射信号通道的偏置电压有效地调整发射功率。通过增加温度传感器，MCU能够更进一步提高RF功率管理系统的精度。只要检测器具有可重复性的温度漂移，对某些测量值的误差补偿是可以实现的。可将考虑到环境变化的补偿算法程序集成到MCU的决策程序中以显著减少或消除制造工艺和温度变化。例如，如果一个功率检测器具有可重复性的温度漂移，那么为了消除已知温度下预期的误差可采用一种补偿算法。

图6示出许多对数放大器的对数一致性误差曲线。在3.5 GHz，温度漂移从+1 dB扩展到-4 dB。器件在-40°C时的总体分布曲线紧随25°C时的曲线。相反，在+85°C 的该分布曲线移动了2.5 dB，并且不再与25°C时的分布曲线平行。尽管在这个频率处的温度漂移很大，但在每个特定温度下的分布保持的非常接近。由于这些飘移的可重复性，所以能够实现一种补偿方案显著提高精度。

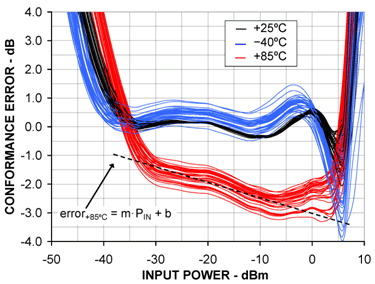
图6. 在3.5 GHz 处+85°C时的温度漂移分布曲线移动并不再与25°C时的分布曲线平行。
通过+85°C对数一致性曲线的线性区的趋势线表示该温度的误差模型。

由于斜率和截距随温度变化导致温度漂移。鉴于这种认识，通过分析器件的总体分布曲线可以总结出一个误差模型。可以建立分布曲线随温度移动的误差表达式，如图6所示。图中画出的通过+85°C对数一致性曲线的线性区的趋势线——误差线，它表示在+85°C时的误差模型。应用该误差线的斜率和截距特性，利用补偿函数关系可抵消这种温度变化。尽管如此，该误差模型仅描述+85°C时温度漂移带来的误差。

大多数的温度漂移发生在+25°C和+85°C之间。对所有温度都普遍适用的误差函数可利用一个温度比例因子k(T)来建立各种温度范围的函数关系，其中k(T)是温度的函数。将补偿误差函数和温度比例因子函数结合起来，组合结果如图7所示。当温度升高的时候，比例因数将跟着变化，从而可消除由于温度漂移上升引起的误差。

图7示出AD8312采用上述误差补偿方法的对数一致性分布。误差补偿前，对数一致性误差为5 dB。误差补偿后，在从-30 dBm 至 0 dBm功率输入范围之间，在整个工作温度范围内对数一致性误差提高到大约±0.5 dB。这种RF功率管理系统可达到的精度是由器件的总体分布曲线确定的。同样的结果对于温度漂移不显著的低温和低频情况也可适用。

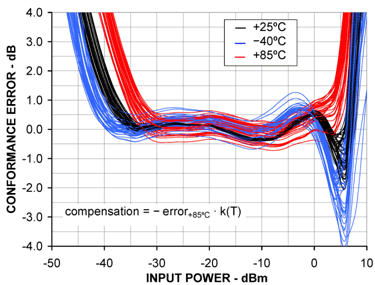
图7. 用补偿误差函数抵消温温度变化引起的误差。
用误差补偿改善整个温度范围内的对数一致性误差。