Increase K factor for stability
Your question is way too broad to answer, because the K factor depends on various factors. egs matching networks, output caps, feedback paths etc. Anyways you could play with source inductance and see what happens.
You can always stabilize an amplifier by doing things you definitely want to avoid.
Simply putting resistance in the source can have a profound effect, such as allowing almost all impedance matches to be unconditionally connected.
The price is it introduces a part that has a thermal noise component. Any resistive dissipative thing badly messes with the noise figure. The slight inductance in the source grounding vias can be augmented by some deliberate inductance - up to a point. This kind of feedback from inductive reactance at least has the good thing that it does not introduce much noise. putting "just enough" of low value resistance in the source might well give you stability while having the noise acceptable
A resistance, possibly part of a bias circuit, from gate to ground via a decoupling capacitor in effect can terminate the input, and make it real stable. The price in terms of noise figure is horrific!
Sometimes, quite usefully, a low value resistance can be put in series with the drain output. This can bring the impedances seen by the FET into the conditionally stable region, without too much effect on the noise.
Using selective feedback from drain to gate, possibly also using part of a bias route can be used to overcome the way the FETs can have extreme gain, and oscillate unstable at very low frequencies well outside the band you want to use. Placing a high value inductor in series can make the network "go away" at the higher frequencies you want to use.
Getting a FET stable is not trivial. Also K>1 is not enough. It may only allow conditional stability. Become familiar with other criteria like |delta|, B1, B2 (if you use ADS) and the more general criteria like MU(source) and MU(load) (if you use MWO and others).
Most designs have stability criteria exceeded at some frequencies, but are successful because the connected parts do not permit impedances that stray into the bad zones. These care "conditionally stable". Designs where the unstable regions are entirely outside the Smith Chart circle are "unconditionally stable"
Keep in mind you have to get the circuit to be stable at ALL the frequencies it has gain. Do not use a FET that still has gain far beyond the highest frequency you want to use. Do everything you can to trash the gain at frequencies you do not want, especially on the low frequency end, meaning all the way down to DC! Do this without noise additions - if you can.
Generally you have to make your input matching circuit have impedances that make the trade-off between input match and noise figure, while staying out of the unstable area on the Smith chart. This also applies to the matching arrangement on the output, and its effect on the input. It is a hard trick to do - without resorting to resistors.
I had a problem with amplifier, even when copying PCB design of working one. So i comed to conclusion: without extensive simulation or many trial and error tuning it is a difficult task. It is interesting to see, that some designs are do not altered for years, if empirically tuned with success.
Ideas i found useful:
- change active device, search for one with more "friendly" S-parameters
- use class C amplifier in pairs with negative biasing, balanced amplifiers, etc.
- copy other design
- sometimes can still be conditionally stable (surely even some commercial products do that)
- make distributed amplifier by connecting many unconditionally stable smaller amplifiers with power splitters/combiners
Hi Darktrax and Terminator3 ,
As you guys have mentioned satisfying Kfactor, MUprime ,MU and verifying phase information doesn't predict the instabilities in real time. I had to re-create a RFPA design which had instabilities even without RF excitation. So, to investigate I re-created the schematic and tried to the fit the model with measured. It was pretty obvious how much ever I try and refine my design to reality I failed. It's frustrating when there is no reference level for the abstraction level of the circuit design close to reality.
What active device do you use?
LDMOS models
did you tried to add resistor as suggested before?
Yes, I have a source resistance.
My simulation of the re-created design shows unconditional stability. Which is in contradiction with the measured result (obvious ). My objective is to re-create some of the large signal instabilities like AM-AM.
Maybe resistance have impact on your s-parameters, acts like a stub in reality, making K even worse. I prefer source grounded very well, otherwise i always have oscillation. Try other place for resistance, or change simulation (add some tiny microstrip pad to resistor, etc.)
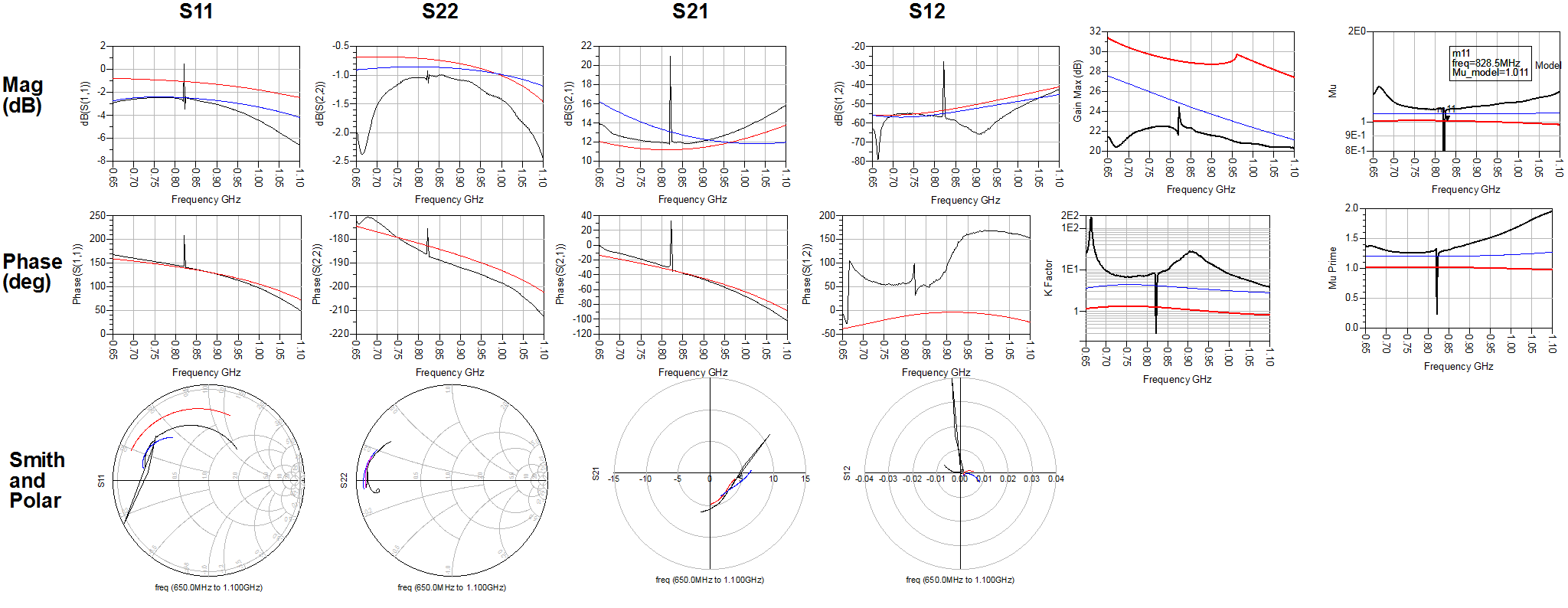
Ok. The black line shows the measured result and other two colors shows the re-created model. See the spike at 820 MHz.. That's the instability .
Hi BMR
To be clear - you built the circuit and measured it, and it was oscillating at 850MHz?
Given that the K-Factor is near 1 everywhere, and the gain characteristic is smooth across the 850 region, it might indicate the oscillation is from unwanted coupling across your layout, or maybe is part of what you attached to measure. Ground plane common mode routes, screening, etc. There are lots of ways this can happen.
Ok let me be as clear as possible. The measured response ( Black line ) was designed by someday else. I just had the package which has pre-matched networks and a die ( fingers = 175 , output power = around 250 W ) So from the die orientation and bond diagram I re-created the circuit to see if I can see any instabilities. So as you can see from S -para results I tried to fit the measured data with the re-created models.
Did you solve this problem?
From my little experience, it reminded me oscillator simulation, where certain length of drain stub made such "spike", wich surprisingly did not moved wen changing gate stub length, but phase around that spike was moving as expected, according to input phase, gate length and s21 phase of FET. But in your case simulation have no spikes, but reality does. I would try: if there any, change decoupling capacitor to other value, changed length of input/output paths.
Thanks for getting back.
No, I did not solve the problem. Yes, I have tried almost all combinations to elements to see something abnormal, but nothing. What I also want to know is is it really possible to derive such a kind of a spike in simulation ? Otherwise I am just wasting time.
It feels like wasting time. Maybe you can put this question in background mode, while do some progress in other parts.
Maybe somebody post a reply later, who knows
I would have only very limited time to try and wring the truth out of this one, but Terminator3 is right - for a chance at crowd-sourcing some insights, it would help if you let us know exactly which LDMOS device you are using, some link to S-parameters or model package if not the S2P files themselves, and the circuit stage(s) you are trying to put around it, and what is the application (driver, power amp, etc.)
Also, which simulation package you are trying to apply. Probably you will get hints, indications, and advice of experience that may get you there.
Thanks for the help, but I would be in a way wasting everyone's time because the circuit is quite huge and complex with hierarchical nature and derived from Assembly diagram.
Anyways I solved the problem by introducing a feedback from the drain side to the source side. Also I introduced a small resistance in the feedback path. So, when tuned at even mode harmonics I was able to see the spikes. So, somehow there is a feedback path + resistance is introduced.
