noise figure definition for IQ
Recently I've been reading this paper where the receiver has two differential output for I and Q channel respectively. The analysis simply assumes an output of I+jQ, but this is a complex signal. How do you measure the noise figure? Is there any instrument for analyzing complex signals?
Thanks :)
Complex signals can have a mean and a standard deviation just like real signals, and therefore their noise and SNR can be quantified in a similar way. However when defining NF you have to specify the input(s) and the output(s) of the chain to know how to measure correctly, and you haven't clarified this.
A IQ signal pair is essentially the same RF signal, but one delayed in phase by 90 degrees.
The RF itself may be phase modulated many ways, (QPSK, DQPSK, etc) or could be amplititude modulated,
but however complex, the I and Q signals are both analogue RF. They will have a carrier level (C).
They will also have noise, and the signal-to-noise ratio is expressed in the conventional way.
When modulated I-Q signals are used for data, usually by one of the various forms of phase shift keying, and the noise causes bit errors, one can use the data equivalent of SNR known as Eb/No.
https://en.wikipedia.org/wiki/Eb/N0
It is directly related to the conventional C/No (Carrier-to-Noise Ratio) by the data rate and the channel bandwidth.
I think, in the context of your question, the SNR of the signals after being added is the SNR they had before, modified by the noise contribution from the dissipative loss of the combiner, ie. the standard change that happens to any signal taking loss from an attenuating device.
Thanks for the reply, mtwieg.
Let's say take the noise from a 50ohm source as input and this I+jQ as the output, what would you suggest to characterize its noise performance? And how do you measure it?
- - - Updated - - -
Thanks for the reply, darktrax.
I am confused how do you combine I and Q together to represent I+jQ properly. What I first guess is simply shift the Q channel by 90 degrees, then perform a normal add. But this gives you a real signal instead of a complex one. The complex signal's spectrum is not necessarily symmetric, thus you do not need to worry about noise from the image in a mixer, right? This paper I mentioned simply use an output of I+jQ and gives the measured noise figure, that made me wonder how they did it.
Noise characterization of a digital receiver is just simply to measure BER at the output while input signal level is decreased.It will give you Noise Performance of the system.
Again, you have to describe your signal chain more specifically. Is your input a single RF signal, or is it already in the form of an IQ pair? Is there frequency conversion involved?
For a simple case, such as a direct downconversion chain, if you measure some noise figure from the RF input to either one of the baseband outputs (this should be the same for both the I and Q signals), then I believe the NF of the path from RF to the complex combination of I and Q should be the same number. This is assuming that both the noise and the signal of the I and Q paths are uncorrelated.
I think my colleagues are all in error. The important facts are below:
1. Noise figure relates to the thermal noise power.
2. I and Q relate to the SIGNALS transmitted.
So there is no sense in relating the noise figure to SIGNAL parameters. Signal I and Q vectors are separated in a receiver in a NON-linear demodulator while the noise figure is a parameter related and measured in the LINEAR section of the receiver, before any non-linear element like demodulator or detector.
Depending on the modulation/demodulation scheme (ASK, FSK, PSK, OFDM, etc.) the signal-transmission parameters are related to the thermal-noise power in the channel. Only then the signal-to-noise ratio becomes important, and it defines the error rate. But receiver noise figure only affects the signal-power budget of the complete radio link. One can counter a poorer noise figure by increasing the transmitter output power,or the gain of antennas.
Whatever you look for Noise Figure before demodulator, or including the demodulator, you have to relate Noise Figure to the SIGNAL, because by definition Noise Factor is the ratio of SNR_inp over SNR_out.
For measuring Noise Figure of the receiver looking at the IQ output, the best way is to do a BER test, because BER is direct related to the SNR of the circuit.
You cannot talk about S/N without talking about noise bandwidth.
It is important to understand the noise bandwidth from each of the I or Q channels separately. The bandwidth of the a filter on each of the I and Q channels are half the overall receive bandwidth. This is because the I and Q contain both positive and negative sides of the center of original input signal. When the I & Q channels are recombined the resultant bandwidth of the signal is twice the I and Q bandwidth.
If the I & Q mixer and I/Q baseband amplifers have no degradation to S/N due to their noise contribution then the recombined I/Q equals S/N of the original signal in its noise bandwidth. Real world noise figure/noise temp degradation by mixers and amps apply just as they do for non-I/Q stages.
Dear vfone, I think you definition of NF is wrong. My definition is:
NF = noise power of a real two-port/ [noise power of an ideal two-port] = k.B.G (To+Tr)/[k.b.G.To]= (To+Tr)/To, where To is the ambient temperature and Tr is the receiver input noise temperature.
No signals are involved but the bandwidth is important.
I must say that BER test is a RESULT of a SNR, not the reverse. BER differs widely for various signal-modulation types while SNR is a PRIMARY quantity in a communication system, only defined by the power budget [S] and thermal noise [N].
If you talk about I and Q signals, you can take any of them (usually I is considered "straight") while Q is phase-shifted 90 deg against I. I and Q signals are only related by signal-modulation type and should be equivalent in SNR evaluation.
- - - Updated - - -
The other proof of NF definition is that NF is NOT measured by measuring signals but by measuring the noise power (ratio).
If you try to measure the NF by SNR by your definition, you will find the NF as a function of signal level, bandwidth etc.
This is why all NF meters and systems utilize noise only.
I found that many people make this confusion between Noise Figure of a Device, and Noise Figure of a Receiver. Actually some of them are going even deeply, confusing Noise Figure with Noise Floor.
I am quoting from one of the most relevant Noise Figure papers written by HP in 1970:
"Although the system bandwidth is an important factor in many systems and is involved in the actual signal-to-noise calculations for demodulated signals, noise figure is independent of device bandwidth."
For Direct Conversion Receivers with IQ output I assume that about 90% o the RF engineers use BER (or similar approach) to measure the Noise Figure of the Receiver.
Oh Dear - you are all "right" in so many ways, but I see sometimes the same terms are appreciated as having different meanings.
For me..
1) A BER is useful as a measure of receiver performance, and is indeed affected by the amount of noise present, but it is not the Noise Figure itself.
2) A signal is a signal. That it may have a phase (I) relative to another (Q) does not suddenly make it a "digital" quantity, just because these phases when shifted about with various modulations ofetn, but not mandatorily, represent digital changes.
3) The bandwidth is always important, from the fundamental relation to temperature and Boltzman's constant, and whether or not the noise came from a dissipative thing. Since BER is a consequence, not a fundamental, expect BER to be bandwidth-dependant also.
You measure the signal to noise ratio in the conventional way, the amount of signal, to the amount of noise. The Noise might all be thermal, or it can include other unwanteds, like galactic sky noise, and unwanted coupled ground noise at 290K, and even other interference. The point is, it is unwanted, and it is analogue in nature, even if it is racket from something digital.
4) When you get to using BER as a figure of merit for a whole system, it cannot be done without reference to the signal level, and the system noise. The useful way, as I said, is to appreciate Eb/N0 to account the bandwidth et al, and then account for the modulation with something like what is in the picture.
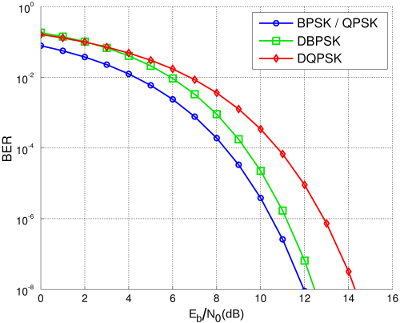
Looking back at it, I agree entirely with jiripolivka.
Usually I never argue on the Internet, following an old Latin quote: "Adversus solem ne loquitor" which can be translated as "Don't speak against the sun".
Always I try to point my answers EXACTLY to the original post, and do not diverge discussion to things that have close OR different meanings.
So, the original post was about: "...the receiver has two differential output for I and Q channel respectively...How do you measure the noise figure? Is there any instrument for analyzing complex signals?..."
My answer was: Use a BER test because BER is direct related to the SNR of the receiver. As somebody mentioned above, BER gives information about Noise Performance of the receiver, which I totally agree.
Some measurement instruments have IQ noise measurement options . If you want to simulate the NF of an IQ system, then you indeed run into the problem of the definition for input and output, because in most software you can specify only one input and one output .
The solution is to create a noiseless IQ splitter at the generatore and an IQ combiner at the output. This way the overall testbench has again only one input and one output.
These splitter/combiners need to do the 90° phase shift, e.g. via LC network (narrow-band) or via Hilbert transformer (wide-band 90°-shifter). In modern simulator like Spectre this is no problem - and all ends up in a slightly extended normal NF testbench.
Just the splitter and combiner are doing the job of adding the signals correctly and automatically (and the noise as well), and NF measurement remains mainly an SNR measurement.
Only few things become more difficult, like having also noise circles, because we would have "I and Q Smith charts" (which may even depend on each other), so nobody is doing so.
Bye Stephan
