Sensitivity or selectivity - How does external LNA impact the receriver performance

it describes

1. Why need external LNA ?

2. Why does poor linearity lead to poor sensitivity ?

3. For the eLNA gain, the more the better ?

4. Why can SAW filter improve linearity ?

1. The noise contribution of each device in the signal path must be low enough that it will not significantly degrade the Signal to Noise Ratio. According to Friis noise figure equation, the biggest contributor to the noise figure of a receiver is the first component in the chain, which usually is the LNA .
https://en.wikipedia.org/wiki/Friis_formulas_for_noise
2. Linearity, and especially the 3rd order non-linearities, because their components arrive inside of the receive band (near the desired signal) they would affect the receiver sensitivity.
3. Also according to Friis noise figure equation, higher the gain of the first component in the chain (LNA), lower the receiver noise figure.
4. Some non-linearity components can be be filtered out using front-end SAW filters, but some components would be hard to be filtered.

[QUOTE=vfone;1467973]1. The noise contribution of each device in the signal path must be low enough that it will not significantly degrade the Signal to Noise Ratio. According to Friis noise figure equation, the biggest contributor to the noise figure of a receiver is the first component in the chain, which usually is the LNA .
https://en.wikipedia.org/wiki/Friis_formulas_for_noise





『the biggest contributor to the noise figure of a receiver is the first component in the chain, which usually is the LNA .』

Sorry~! The former is right, the later is wrong.

If so, it means you will have two biggest contributors if you add an external LNA (eLNA). By doing this, with eLNA, the sensitivity should degrade instead of improving.

But, in every cellphone(including the cellphone you are using now, and the latest iPHONE 6S and 6 plus S), the GPS must have one eLNA. Why do we degrade its sensitivity further by adding an eLNA ?

Besides, if the LNA is the biggest contributor to the noise figure,
it should be called “HNA”—High Noise Amplifier, instead of LNA.

In fact, eLNA does improve sensitivity, that is why the GPS in every cellphone must have one eLNA.

http://www.mpdigest.com/issue/Articl...el/Default.asp

The LNA (due to is gain) improve the receiver sensitivity, but due to its inevitable noise figure will also decrease a bit the receiver noise figure. Just add some numbers in the Friis equation and you will understand.

So an LNA, MUST have gain AND very low noise figure, both in the same time, otherwise instead of improving the receiver noise figure it will degrade it.

All right, so you know things. iPHONE 6s and Plus use LNA's. I am little bit confused. What about iPHONE 4, or Samsung 4 mini, or the old Nokia 6121, do they use LNA's?

It seems that you want to answer questions in your attached PDF ... and created confusion because your post with all the questions looks like student's homework questions.

I am the original author.

Yes, what I wanted to express is that you can find the answers to these 4 questions in the attachment.

The question and answers are not correct generally. The comunication SYSTEM must be considered complete. Improving receiver alone by inserting a LNA can result in system degradation, due to a higher non-linearity and a higher interference level, intermodulation, etc.

Okay! I just start the following discussion from the simplified Friis equation:

According to the equation, the overall noise factor,

,
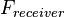
is dominated by the noise factor of the LNA,

.
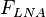
If the gain is sufficiently high, LNA subsequent stages have a diminishing effect on signal-to-noise ratio(SNR).


So far, this is right, just as what you said previously.
But, the situation only occurs when LNA is the first stage.


Let’s return back to the original Friis equation.

In fact, in real signal chain, LNA is not the first stage(F1),
because there are some components(e.g. ASM, SAW filter, etc. ) , including PCB layout trace and connector, in front of it.
In other words, the biggest contributor to the noise figure is hardly LNA,
but those components in front of LNA. They are the real F1 of Friis equation .

So, why can an external LNA (eLNA) improve sensitivity ?
Take the following two cases for example

Without eLNA :

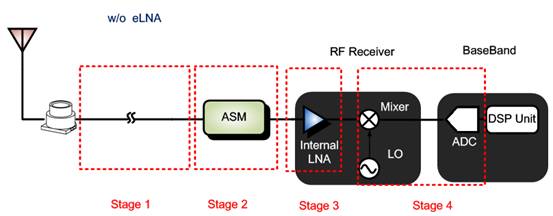
With eLNA :

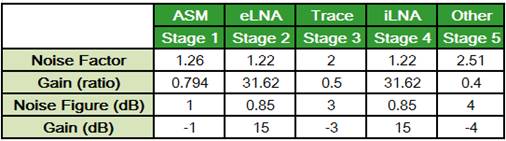
As calculated above, their noise figure are :

Without eLNA : 5.04 dB
With eLNA : 2 dB
Improvement : about 3 dB

Again, the eLNA really improves sensitivity.
If we analyze the two cases in detail, we can find that the improvement is due to the reduction of F1 of Friis equation.
As illustrated below :

Without eLNA, the insertion loss of layout trace is part of F1 of Friis equation,
and increases cascade noise figure directly.
But, with eLNA, the insertion loss of layout trace is not part of F1 of Friis equation.
As mentioned above, LNA subsequent stages have a diminishing effect on SNR.
That is to say, with eLNA, the insertion loss of layout trace hardly affects the sensitivity.
Therefore, 3 dB improvement is due to the insertion loss of layout trace (3 dB).


Conversely, if the location of eLNA is shown as below:

The sensitivity doesn’t improve because the F1 of Friis equation is the same.
Unless, noise figure of internal LNA (iLNA) is much larger than which of eLNA so that sensitivity improves because of ignoring the contribution that iLNA makes to cascade noise figure (because iLNA follows eLNA).
Consequently, where you put eLNA does affect how much sensitivity improves.
Of course, the closer to antenna, the more sensitivity improves.



Let’s discuss GPS.
In cellphone, we may make GPS antenna be far away from 2G/3G/4G main antenna to isolate GPS weak signal from other RF signals.
As shown below :

That is to say, the GPS antenna will be far away from receiver.
It means that the F1 of Friis equation is very large, and sensitivity degrades very much.
So we need an eLNA to reduce the F1 of Friis equation, and then improve sensitivity.
It’s the reason why GPS is the RF function that we use eLNA most often.
According to previous analysis, we should put GPS eLNA close to GPS antenna, the closer the better.
Otherwise, the large eLNA Pre-loss due to long layout trace degrades sensitivity much.
As a result, eLNA can’t help us improve sensitivity anymore. As illustrated below :

Besides, while selecting these components in front of eLNA, e.g. ASM, SAW filter etc. ,
their insertion loss should be as small as possible.
Because they are part of F1 of Friis equation, and degrade sensitivity directly.
For example, there usually are pre-SAW and post-SAW in GPS application,
and low insertion loss is the key point of pre-SAW.

In some receivers,
the SAW filter locates between LNA and mixer to avoid degrading sensitivity because of the insertion loss of SAW filter.

A SAW filter is not designed to improve linearity. Often it does as its typical in-band insertion loss is 18 dB or so. SAW filters are small , compact and have good filtering features. But an additional IF gain is needed due to the above.

SAW or BAW are quite common in today's front end module for mobile phone to get rid of out-of-band signals.
http://en.tdk.eu/tdk-en/373388/compa...phones-/170556

If the Low Noise Amplifier (LNA) is not the first stage its name is simple: AMPLIFIER.

Still I don't understand why criterion456 is answering to the questions of Da CHi Wang, if they are the same author.

All radios with good sensitivity must use a low noise front end with some bandwidth limiting. As the gain of input noise exceeds the input noise of the next stage, it becomes the one of the dominant factors. The next dominant and essential factor is adjacent channel rejection or selectivity, where the ratio of signal/unwanted signal in the 1st IF band is improved by the BW of the 2nd IF BW. The end result is the optimum design includes the highest SNR with minimum THD, LO Leakage, and adjacent channel(s) rejection. For data, ISI from group delay distortion is a critical factor for the "optimal Receiver"

FBAR or TFBAR are the ideal choice above a 1~2 GHz
http://www.avagotech.com/products/wireless/fbar/

Okay ! Let’s discuss linearity next.

Still start the topic from Friis equation :

According to Friis noise figure equation,
higher the Gain of LNA, lower the receiver noise figure.
Therefore, when received signal is extremely weak,
we need to activate High-Gain Mode to lower cascade noise figure to posses acceptable sensitivity.

Nevertheless,
Friis noise figure equation also tell us that F1 is the most important factor instead of gain of LNA. If F1 increases 1 dB,
then sensitivity degrades 1 dB directly at least.
It’s the reason why that the location of external LNA (eLNA) is very important.
As illustrated below :

In above two cases, the gain of eLNA are both the same, but sensitivity improvements are quite different.


Nevertheless,
some people may think that eLNA gain is still the higher the better, even if its influence is no match for F1.

This is wrong.
Because higher the gain , lower the receiver linearity.
And poor linearity leads to poor sensitivity as well.

As illustrated as below :

Without eLNA :

With eLNA :

Let’s calculate their cascade IIP3 and noise figure,
and compare the difference between w/o eLNA and w/ eLNA.

We observe that eLNA makes the cascade noise figure of receiver degrade (5.04 dB => 2 dB),
then improve the sensitivity, but the IIP3 also degrades(-26.5 dBm => -41.6 dBm).


In fact, according to cascade IIP3 formula,
we can also find that higher the gain , lower the IIP3 .
And according to following document :

Improving Receiver Sensitivity with External LNA - Application Note - Maxim

we know that the IIP3 degration is due to eLNA gain.

Take the above cases for example,
let’s plot the relationship between eLNA gain and noise figure, IIP3 :

We can observe that the noise figure reduction due to eLNA gain is limited.
But, the IIP3 degration due to eLNA gain is unlimited.
Take the plot for example, when the eLNA gain is larger than 15 dB, the cascade noise figure is almost the same.
But, the IIP3 still degrades.
And the IIP3 degration is inversely proportional to eLNA gain linearly,
as the eLNA gain increases 1 dB, the cascade IIP3 also degrades 1 dB directly.


Perhaps some people may ask :

“At least, higher gain doesn’t lead to higher noise figure, why do I have to care IIP3 degradation ? ”

Indeed, according to sensitivity formula :

IIP3 seems to have nothing to do with sensitivity.
Nevertheless, in reality, we have to consider noise.

Let’s assume there are 2 tones with nearly same frequency,
f1 is interference, f2 is signal, f1 is closer to f2.
If LNA IIP3 is not good enough,
there will be 3rd order intermodulation (IMD3), which is near desired signal and can’t be filtered, degrading SNR all the time.

Besides, there is Tx leakage issue in WCDMA, CDMA, and FDD-LTE :

Therefore, there will be three signals in the receiver input : Blocker, Rx signal, and Tx signal :

Because as long as two signals can produce IMD.
That is to say , if the IIP3 of receiver is not high enough,
the strong Tx signal saturates receiver, the desired signal will be interfered by IMD easily.
For example,
Tx signal of WCDMA Band1 (1.95 GHz) and Tx signal of DCS 1800(1.76 GHZ) can produce IMD3,
which will interfere Rx signal of WCDMA Band1(2*1.95 GHz – 1.76 GHz = 2.14 GHz ) .

As illustrated above, poor linearity leads to poor sensitivity as well.
Therefore, the eLNA gain is the trade-off between linearity and sensitivity,

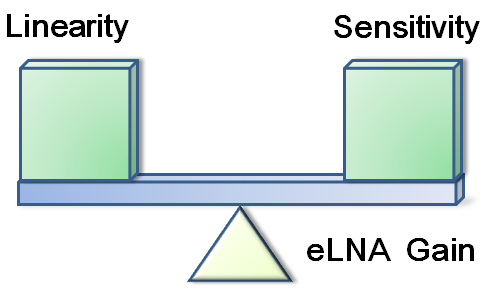
we should consider sensitivity and linearity simultaneously.
The eLNA gain is neither the more the better nor the less the better.
It should be the more exact the better.





No~! Even if LNA is not the 1st stage, its low noise is still necessary.



As analyzed above,
LNA subsequent stages have a diminishing effect on signal-to-noise ratio(SNR)
That is to say,
for the cascade noise figure calculation,
we just need to focus on the stages preceding LNA and LNA itself.

Let’s illustrated as below :

As calculated above, we know that the cascade noise figure is 2 dB with external LNA (eLNA)

According to cascade noise figure formula :

the total insertion loss of these stages preceding eLNA is just F1.
If we simplify the cascade noise figure calculation further,
merely add F1 and eLNA noise figure together, and compare the result with previous calculation :

As shown in above table, the calculation of simplified method is almost in concert with previous calculation.
Consequently, we can simplify the cascade noise figure calculation as following formula :

Noise Figure(dB) = LNA Pre-loss(dB) + LNA Noise Figure (dB)

Of course, F1 dominates the cascade noise figure,
but it doesn’t mean that noise figure of LNA doesn’t matter.
Higher the LNA noise figure, still higher the cascade noise figure.


Therefore, even if LNA is not the 1st stage, its low noise is still necessary.

Of course, the purpose of SAW filter is to reject out-band noise.
Nevertheless, it can really help us improve cascade IIP3 of receiver by means of its selectivity.

As illustrated above, the selectivity means its ability to reject out-band noise.
Let?s take a simple 3-stages circuits for example,
if we add a SAW filter, its IIP3 calculation is as below :

As illustrated above,
SAW filter subsequent stages have a diminishing effect on cascade IIP3 because they have selectivity of SAW filter, S^(3/2),
in their denominators.

Therefore, we add a SAW filter with 40 dB selectivity in front of an external LNA(eLNA) with 5 dBm IIP3,
and compare the IIP3 variation :

As calculated above, we find that the IIP3 is from 5 dBm to 67 dBm.



In other words, if the linearity of LNA or mixer is not good enough,
you can put a SAW filter in front of it to relax the linearity requirements of the Rx chain.


FILTERING LOW NOISE AMPLIFIERS FOR SAW-LESS CMOS RECEIVERS



Of course, in theory, BAW or FBAR is better than SAW,
because they have better selectivity than SAW.


Therefore, SAW filter can?t reject in-band noise, though.
Nevertheless,
you still need to put SAW filter in front of LNA with poor linearity to improve its IIP3 to suppress IMD3 that is near the desired signal and caused by LNA nonlinearity.

According to cascade IIP3 formula,
later the stage, more effect on cascade IIP3.

That is the reason why mixer has higher linearity requirement than LNA.
Thus, some mixers adopt passive form to posses higher linearity.
And in some receivers, the SAW filter is inserted between LNA and mixer,
the aim is to relax mixer strict linearity requirement without increasing the cascade noise figure due to its insertion loss.

As mentioned in previous post, there are usually pre-SAW and post-SAW in GPS application,

Low insertion loss is the key point of pre-SAW based on noise figure,
but high attenuation is the key point of post-SAW based on linearity.


Conversely, if the LNA and mixer have excellent linearity,
the SAW filter is not necessary. This is the reason why some receivers are SAW-less design.


A Multi-Band WCDMA SAW-Less Receivers with Frequency Selective Feedback Loop

These are RF architecture basics and we would expect designers to be aware of these dependencies. But anyway, still useful for non-RF guys to see the math applied to "real" systems.



... but wait. I don't agree on the first part of post #14 part where your SAW increases the IIP3. I think your math/data is flawed there, because the SAW will pass an entire band.

Please see the article

Use Selectivity to Improve Receiver Intercept Point

How is this related to your example? Maxim use SAW in the IF (not RF).