Input reflection coefficient

Hello.
To get the reflection coefficient at the input (port 1) of a two ports device knowing its scattering matrix and the load at port 2 one can use the formula

, but I don"t quite get it. I can see that when a wave enters the device, part of it is reflected back (s11). The remaining wave (1-s11) is free to cross the device and a portion s21 of it reaches the end (the other port). Then, a portion GL (gamma L) of this is reflected back and again the portion s12 reaches back port 1. So far we have

, where c represents how much of the second part can actually exit port 1 due to further reflections to sum it up properly to s11, but i don"t know how to evaluate that.. The formula takes into account also s22, but i don't see how can port 2 affect this since we're at port1..
I have the feeling my whole line of reasoning is flawed, I'd be grateful to anyone able to correct me!
Thank you in advance

The key player is S12 here.If you make it zero, Gamma_in will be equal to S11.
All those equations come from "Mason's Flow" technique.

I already thought about that but never tried because I'm missing something here.
Here I made some hand calculations.

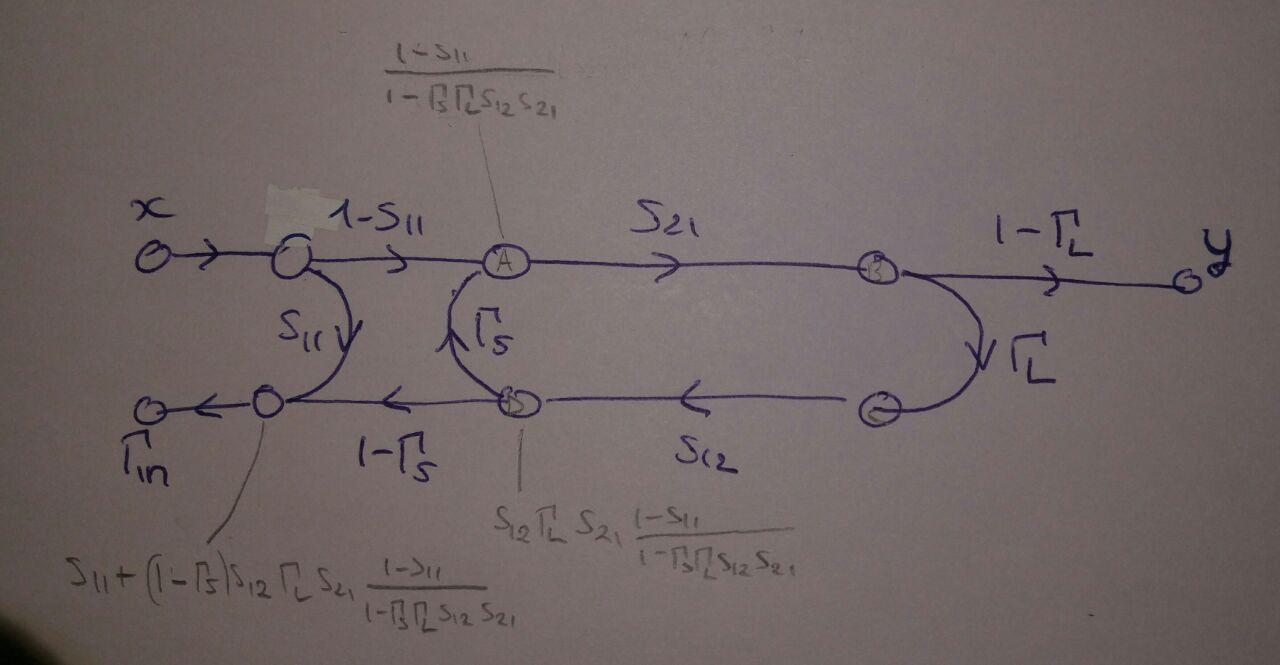
If everything is fine and I use the right value for

(which I don"t know) I should be able to retrieve the previously mentioned formula. So I tried to solve for

by equating the bottom left equation with the formula but I get a long strange expression that doesn"t really mean anything to me...

Gamma_S=0 in normal conditions.
Gamma_S=Source Reflection Coefficient

Turns out there were still a couple of problems on top of that that made the flowchart wrong:
1 - No need to add the (1-s11) branch: it is implicit in the definition of s21
2 - The node I marked C is actually a2 whereas B is b2, so a branch s22 connecting the two nodes is missing
Thank you very much!