Open Circuit impedance and Short Circuit impedance.
If the Short circuit impedance are very close to Open Circuit impedance.
What does that means?
that means The Transformer have very low coupling coefficient?
I don't understand what you mean. Can you, please, elaborate more your question ?
As far as I know, commonly, in Transformer, magnetizing inductance is bigger than leakage inductance.
but the transformer i have, has big leakage inductance ans small magnetizing inductance.
i measured magnetizing inductance like this step :
LCR meter connect Transformer secondary port and primary open.
ans i measured leakage inductance like this step :
and LCR meter connect Transformer secondary port ans primary short.
If you look at the transformer equivalent circuit, you'll notice that it's technically impossible to get a larger leakage than magnetizing inductance. The most plausible explanation is that you have problems to measure it with your LCR meter correctly.
You mean that measuring the secondary inductance with the primary shorted, you get a value higher than the same measurement performed with the primary left open ?
Could you say what value of Lopen and Lshort did you get ?
What about the frequency the measurement has been made ?
not larger leakage than magnetizing inductance.
just as i knew, magnetizing inductance much larger than leakage inductance.
but this transformer has difference characteristic.
to be accurate i have variable reluctance resolver, and i measured variable reluctance resolver.
but VR resovler work as rotating transformer.
so i applied same theory.
here is some information which you required
Lopen = 13.90 mH @ 10kHz
Lshort = 13.85 mH @ 10kHz
thanks to be interested in my question.
Sorry, I didn't read your initial question well. The conclusion seems correct, there's apparently about no coupling.
Consider that the open/short measurement doesn't give full information because it doesn't tell about the coupling sign. You can e.g. measure the total inductance of forward and backward series connected windings to get it.
For the representation of coupled windings, a matrix of self and mutual inductances is helpful, or more general, a complex impedance matrix.
Obviously the measurements must be taken for different transducers angles.
The method you tried to use works only for coupling coefficient k close to unity.
I think you could try to estimate the coupling coefficient, to have a more o less accurate measurment of primary, and leakage inductance. I'm going to explain my idea (however I've never tried).
We can refer to the following model:
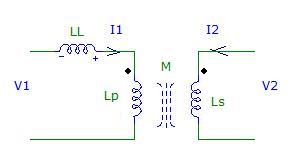
The transformer is represented as mutual coupling M between a primary having an inductance Lp and a leakage inductance LL, while the secondary has a complessive inductance Ls.
The general equations are:
V1=s*(LL+Lp)*I1+s*M*I2
V2=s*M*I1+s*Ls*I2
then the open secondary (I2=0) inductance (i.e. V1/I1), seen by primary will be:
Lop=LL+Lp
Shorting the secondary, the inductance at the primary will be:
Lsh=LL+Lp*M^2/Ls
Now we can connect the windings in antiseries and measure the inductance again:
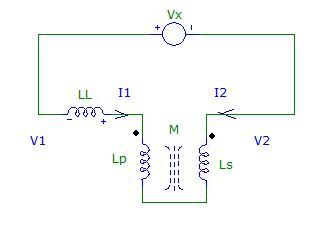
In this case I1=-I2 and the inductance (Vx/I1) will be given by:
Zas=LL+Lp+Ls-2*M
Connecting now the winding in series
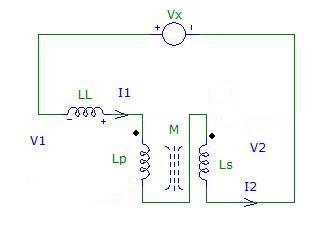
Here we have I1=I2 thus the inductance Vx/I1 will be:
Zser=LL+Lp-Ls
Now from the system of 4 equations, 4 unknown it's possible to estimate LL, Lp, Ls and M:
Lop=LL+Lp
Lsh=LL+Lp*M^2/Ls
Zas=LL+Lp+Ls-2*M
Zser=LL+Lp-Ls
The coupling coefficient is k≈M/sqrt(Ls*Lp).
I hope this method could works. Let me know if you have any result in applying it.
