积分变换基础

一直想对积分变换的内容做一个比较系统的总结和归纳，可能是源于大学对信号与系统的渣渣学习吧。

相信不管是做模拟，混合信号还是射频，《信号与系统》都是基础内容，且重要性极高，难度也很大，相信有不少从小抱着要从事IC设计这种高（搬）大（砖）上（工）专业或职业的人都栽在了学习信号与系统的道路上，侥幸拿到60分的估计考完后再也没有动力捡起来了，像我这种学渣，侥幸入了坑，才发现出来混迟早要还的。既然躲不过，那就硬着头皮从头来过咯。

借这个机会，准备把积分变换的相关内容系统的总结一下，顺便也在好好学习思考。如果单单把oppenheim的书本内容抄过来，肯定会很枯燥，被本科这种填鸭式教学给幼小的心灵留下的创伤之后，肯定不想在被伤害一次吧。所以我试着尽可能用比较少的公式，把相关内容呈现出来。如果在被我写的内容伤害，那可是罪过啊。也表示一下歉意。

作为开篇第一部分，我们先总括的把相关知识及相互关系和基础知识罗列出来。

这里不得不先聊聊欧拉，欧拉（Leonhard Euler，1707-1783），生于瑞士。具有开挂的一生，在18世纪的科学史上留下太多传说。兴趣广泛，成就也很多。其中在复变函数的欧拉公式(Euler's formula)，更是基础内容。

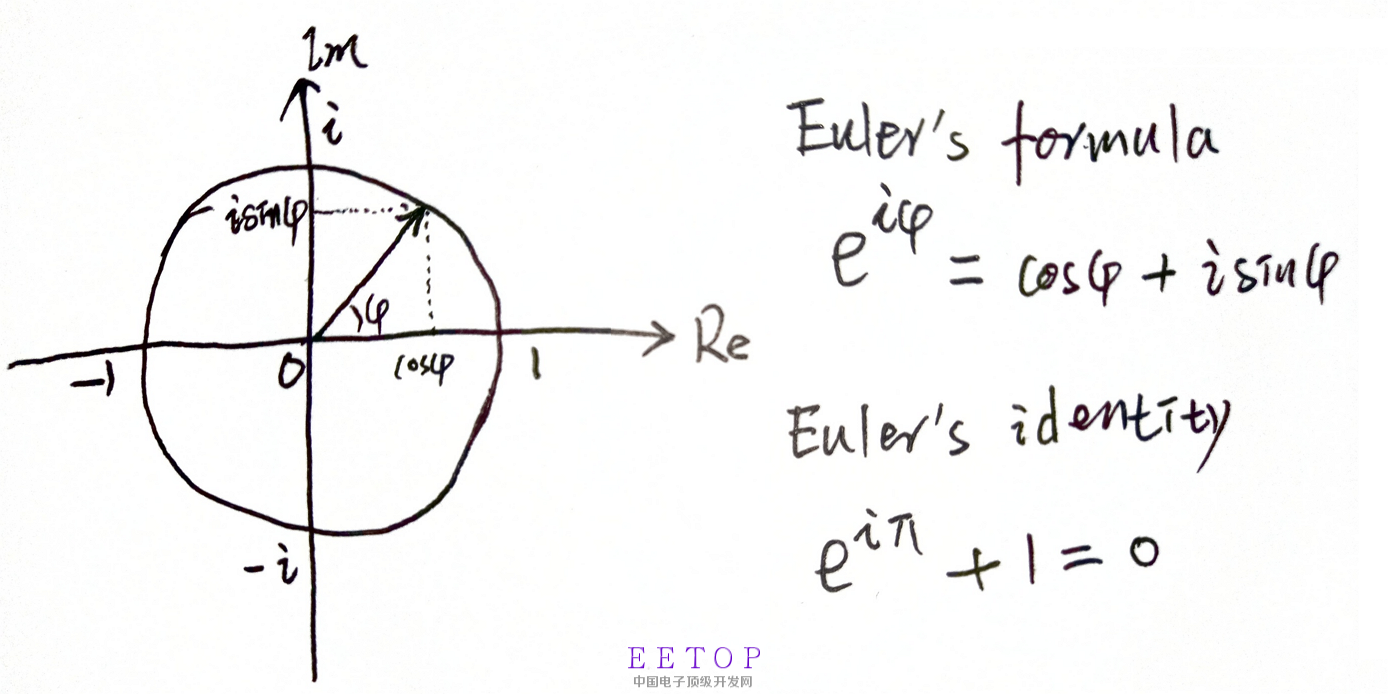
图1

图1中的欧拉公式，建立了复指数(complex exponential)和三角函数的关系。在数学、物理和工程中无处不在，我们要讲的积分变换中会经常见到。该公式可以使用泰勒级数展开进行证明。其中当φ=π
时，欧拉公式进化为欧拉恒等式(Euler's identity)。这是数学中最令人着迷的公式。联系了自然常数e，圆周率π，虚数单位i、实数的0和1。高斯曾有过类似感叹：“一个人第一次看到这个公式而不感到它的魅力，他不可能成为数学家。”尽管我这榆木的脑袋，是没有可能成为数学家啦，但不影响欣赏美的态度。

虚数单位i将实数扩展到复平面，欧拉公式把二维平面的点，从直角坐标到极坐标表示。这里借鉴wikipedia绘出欧拉公式的三维图，红色螺旋线。其在Re平面投影为Cos余弦函数，在Im平面投影为Sin正弦函数。相信大家有学过电磁场会有印象，电磁波的传播过程中，电场和磁场正交。其中红色的部分的螺旋线也有点像DNA的结构，很神奇。

图2

对欧拉公式变型，可以将三角函数表示为复指数的形式，如图3所示。

图3

在18世纪中叶，欧拉在研究振动弦问题时，尝试通过线性组合不同谐波的三角函数来表示质点振动问题。也经过激烈的讨论，有了逐渐认识和完善的过程。其中就包括伯努利，拉格朗日、傅里叶等人。特别是傅里叶在不利的背景下。深入研究了该问题，特别是非周期信号可以表示为不全成谐波关系的正弦信号的加权积分。以此激励人们更深入的研究该问题。为纪念傅里叶的突出贡献，以他的名字命名了傅里叶级数和傅里叶变换。

周期为T的信号，其傅里叶级数表示如图4所示。傅里叶级数系数为ak，其中a0成为直流分量，a±1为一次谐波分量，a±k为k次谐波分量。

图4

对于图4的周期信号傅里叶级数展开，相信大家对课本上的方波信号的展开都有印象，这里举个三角波信号，如图5所示。其中实信号的周期为2，在区间[-1,1]的定义为三角波。傅里叶级数系数的幅度如图6所示。

图5

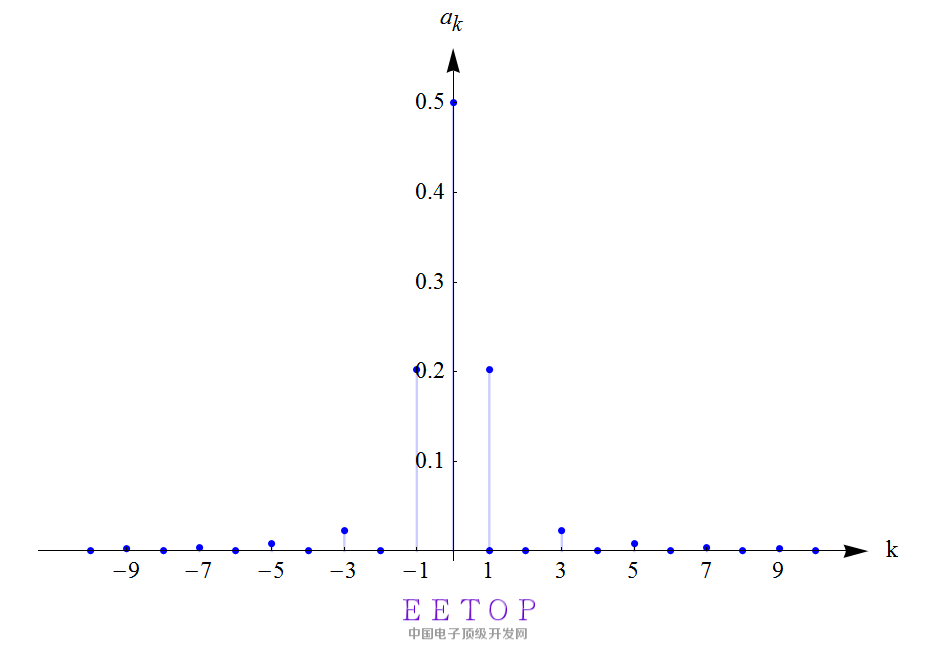
图6

图5中例子，当k=0~7时，在一个周期上，傅里叶级数的直流分量和余弦函数表示如图6所示。

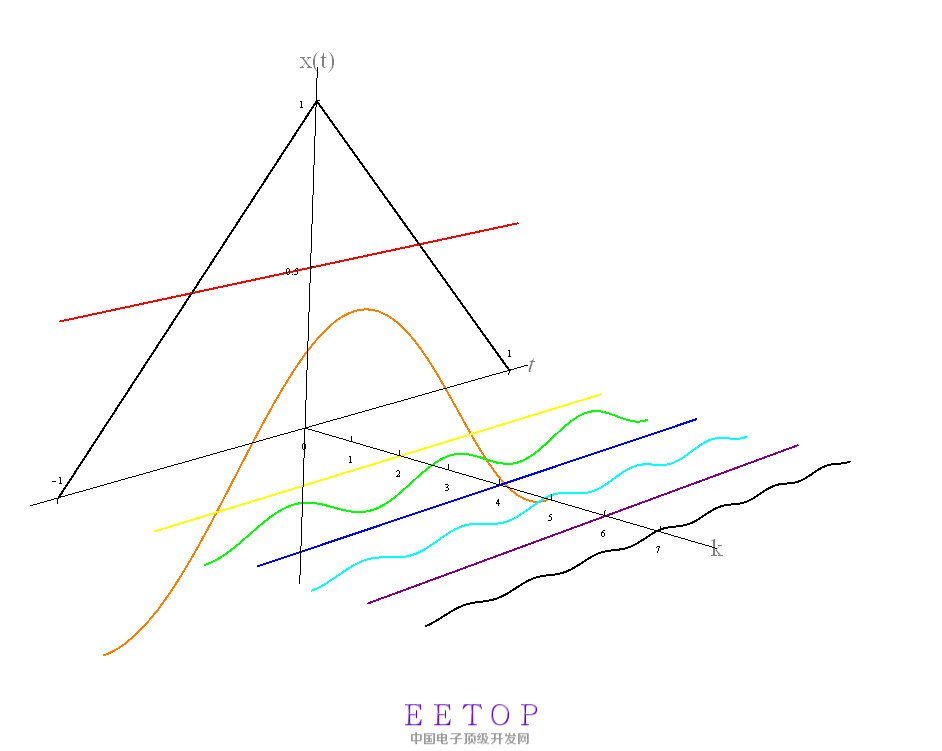
图7

图8给出了当k逐渐增大时，有限k项的级数和的逼近情况。

图8

一个例子怎么能行，课本上有周期方波的傅里叶级数展开，这里再给一个台阶信号及其傅里叶级数逼近的过程。其中蓝色为周期等于1的台阶信号，在t=0.25，0.75和1处存在不连续点。红色为当k增大时，有限k项傅里叶级数表示的信号，灰色
是
红色在t-x(t)平面的投影。可以看到“吉伯斯现象”(Gibbs phenomenon)。在间断点处出现过冲和振荡。

图9

当然，不是时域的任意信号都能够表示的傅里叶级数都是收敛的。需要满足一定的条件。对于傅里叶级数的收敛条件，德国数学家，狄利克雷(Dirichlet，1805~1859）于1829年发表了任意函数展开为傅里叶级数及收敛性的文章。也成为判断傅里叶级数收敛的重要条件。

图10先出"信号"与"系统"的汇总关系图。在时域我们基本能完成信号与系统的所有操作。那么通过积分变换，转换到s域或z域。会有与时域不一样的新特性，和运算的便利性。

图10

想了解更多内容，欢迎关注小牛牛的公众号，一起学习，进步哟~

赞一个

好棒！

复指数(complex exponential)和三角函数的关系。在数学、物理和工程中无处不在