关于Folded-cascode中,input-cascod管子作用的直观分析!
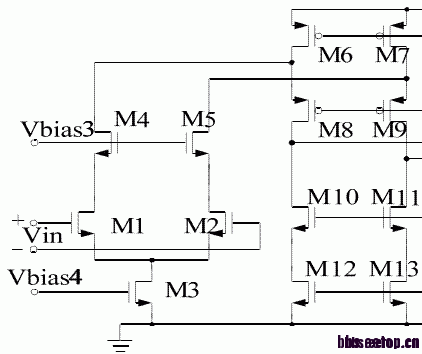 见以前有人询问此种结构中M4,M5(学名:input cascode)的作用,先单独开一贴分析一下。
见以前有人询问此种结构中M4,M5(学名:input cascode)的作用,先单独开一贴分析一下。结论先行:
1. 为了避免输入端的Cgd1和Cgd2,在输入端造成的大的miller电容,如果前级信号源有内阻,这个内阻配合这个输入端的miller电容造成大极点在输入端。
2. 折叠点(M6,M7的drain端)在低频下是一个高阻0.5ro,但是在零极点分析的时候被当做低阻1/gm。
用最直观的方法分析才是好的designer。
首先,我们从折叠点(M6,M7的drain端)开始,从M6,M7drain向上看,看到一个ro;向下看:
a.如果M8,M9drain端向下看的电阻很小的话,则M6,M7drain端向下看的电阻约为1/gm;
b. 但是, 很遗憾,M8,M9drain端向下看的电阻很大为gm*ro*ro,则从M6,M7drain端向下的电阻约为ro(有兴趣可以推导一下)。
故,M6,M7向上向下都看到一个ro,平均电阻ro/2;如果没有 input cascode(M4,M5)相当于,M1,M2的drain端接了一个大电阻(小信号);会产生严重的miller效应;降低电路速度,引入大极点。
加了M3 M4后,从M1 和M2的drain端往上看,看到一个约为1/gm的电阻,有效减少了,输入管的miller效应(假设从前一级的信号源(图中未画出)是有内阻的)。
简单说,input cascode的作用就是为了减少输入管drain端看到的等效电阻,从而
避免输入端miller效应的大电容,配合前级信号源是有内阻,造成的极点。
参考文献 EE240 2009 2013 Folded-cascode 一章 (EE240 2009 Lecture 12 第50分钟处)
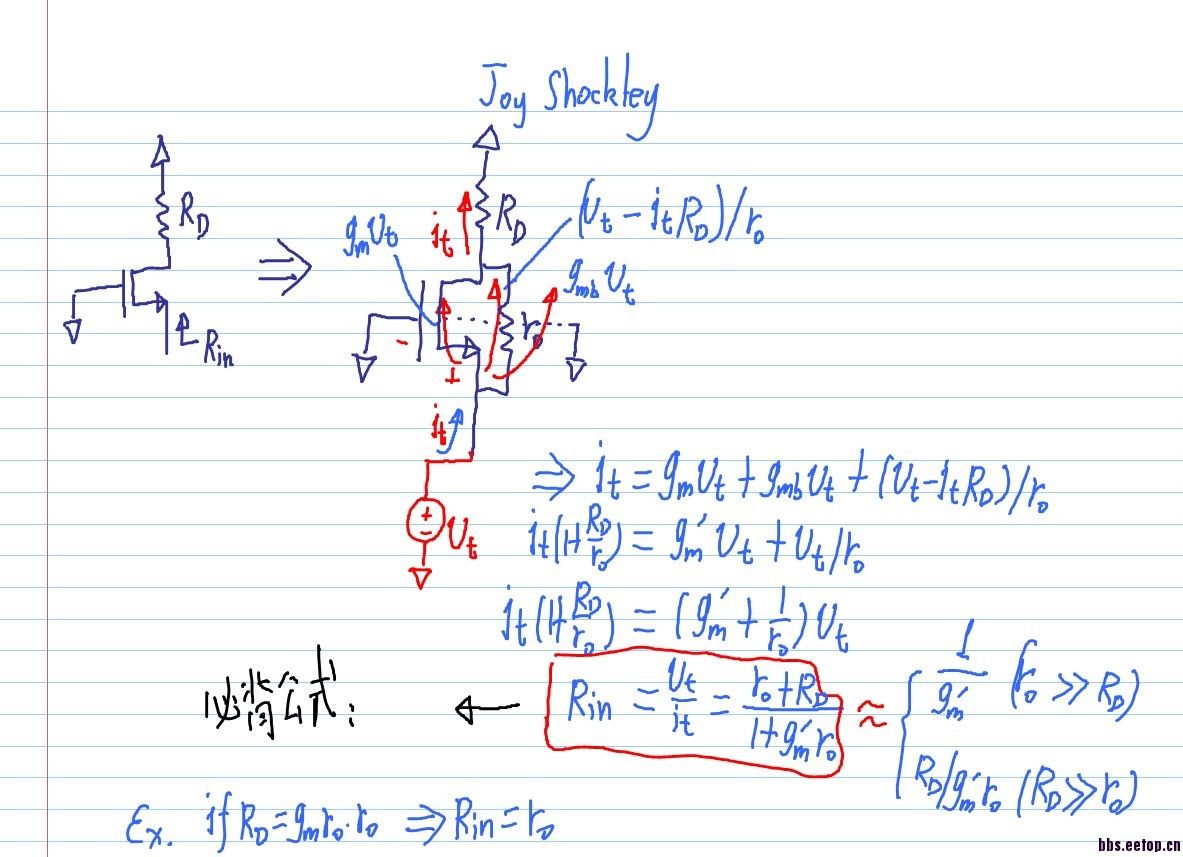
问题2:既然折叠点是高阻,为什么我们在做零极点分析时,却看不到这个高阻配合折叠点的寄生电容产生的极点的呢?
这是因为,在高频时,输出电容近似短路,于是这个点变成低阻点约为1/gm,故折叠点的极点为gm/Cp。详细分析,如下

补充说明:
极点的位置与频率无关,严格小信号分析,次极点的位置应该会和gm,Cp,CL,ro都有关,是一个与他们相关的复杂表达式。
它的大小应该是很靠近gm/Cp,远离1/(roCp),即使CL和Cp在一个数量级。 实际情况往往CL很大,所以它会更加靠近gm/Cp.
在基本folded-cascode-OTA(无input-cascode结构,无信号源内阻)
主极点约在1/(gm*ro*ro*CL)处,应该都没有疑问吧。那上述结构中的次主极点在哪呢?
如果进行详细的小信号分析,是肯定可以得到一个非常复杂的次极点表达式的,它和gm,ro,cp,CL 都有关系,大约有四个。
(四个次主极点在M6,7,12,13的drain位置引入,他们地理位置相近,所以大小相近)
以折叠点为例,这个复杂的表达式所表示的次极点的大小大约是多少?
1. 假设它离主极点很近,也即,在主极点之后的相距不远的频率处,假设此时,CL的作用还不是很明显(极端时认为CL开路),这时该点的电阻约为ro,电容cp
我们预估这个复杂的次主极点位置大概在1/(ro*cp)处。
这样的假设是正确的吗? 我们来看一下,若它在这个位置,则它是主极点大约gm*ro*(CL/Cp)倍的位置,即使输出端电容CL跟Cp一个量级(实际情况要大的多),那这个倍数也有将近gm*ro(=30-40)倍(以TSMC-0.18工艺L=180nm,NMOS为例)。 这个倍数下,放大器的增益,早就降低好几十倍了,说明这个频率下1/(sCL)的值很小了为ro(与gmroro相比)。所以, 我们把输出端电容处理成开路的做法是错误的。
2. 假设这个极点离主极点很远,是一个高频极点,认为此时CL近似短路,此时从折叠点看到的电阻为(1/gm),电容Cp;
这个极点在gm/Cp附近;
它是主点的gmro*gmro*(CL/Cp)倍,假设CL跟Cp在一个数量级,则它主点的gmro*gmro=1600倍数,的确是高频。
在这个频点放大器增益约为1。也就是说,OTA的输出阻抗的大小为1/gm。
回过来看,我们的假设是在次极点时,CL近似短路,也即我们假设在这个频点的输出阻抗很小;在这个基础上,我们推到了折叠点的电阻约为1/gm而非ro。然后,我们导出极点位置,发现在这个极点位置下,OTA的输出阻抗确实很小为1/gm。
自圆其说,类似不动点中f(x)=x,在下一节中会有详细说明。
于是我们接受这个复杂的主极点的表达式的近似值会靠近gm/Cp。
我不知道我是否准确表述了上面的逻辑,看起来有点循环论证。但这种思路是能否定第一种情况的,即这个极点是不可能在1/(roCp)附近
次极点的复杂表达式的值的位置应该是在1/(ro*Cp)与gm/Cp之间,非常靠近gm/Cp,而且是CL越大,次极点越靠近gm/Cp。
再次补充说明:
想到一种用函数不动点 f(x)=x 进行解释的原理:
问题:我们需要知道在次极点处的输出阻抗的幅值,输出阻抗的幅值=(gmroro并联上(1/sCL));由于次极点不知道,所以,这个幅值也不知道。
假设它是满足方程g(x)=0的根;这个方程肯定存在,但是可能非常复杂。为了求解方程,我们把g(x)=0换成 f(x)=x;
“f(输出阻抗)= 输出阻抗”
第一次我们假设x=gmroro,也即认为输出的电容CL,在次极点处完全不影响输出阻抗;在此基础上我们进行一系列推导,发现在这个假设下f(gmroro)=gmroro并联ro=ro,其中ro是此时容抗的幅值。
我们的假设离结果很远,于是我们进行第二次迭代(准确叫第二次猜测);
我们假设在次极点处,CL严重影响输出阻抗幅值。
极端:我们假设在次极点处,输出阻抗为0,也即CL完全短路;在这个基础上我们完成推导f(0)=(1/gm),这里的1/gm是表示的输出阻抗;这个结果已经比上次假设很接近了,所以我们认为此时假设较为合理。
在这样的假设下,我们得到折叠点的极点gm/Cp。、
gmroro大于rox大于f(x)
0小于1/gmx小于f(x)
实际在次极点的输出阻抗可定在ro与1/gm之间;非常靠近1/gm;
折叠点的等效电阻也应在这两种假设之间(CL断路和短路);也即ro和1/gm之间;次极点在1/(roCp)与gm/Cp之间,非常靠近gm/Cp。
可用下面这个图来加深理解
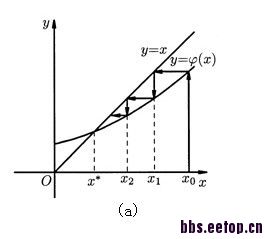
另外我们在求解fT的时候,似乎也用到了类似的思想:
我感觉这样的方法,不想你说的这种情况,比较像不动点的情况。
我们推fT时,假设了在fT时,的输出电流全为gm*vi,实际应是(gm*vi-vi*(s*Cgd));
输入电流为s(Cgs+Cgd)*vi;
两者相等,则fT=gm/(Cgs+Cgd)/2pi;
然后我们会把这个fT的值回代回去,发现vi*(j*(fT/2pi)*Cgd)相比gm*vi的确可以忽略。
这也是一种不动思想的求解方程。
如果没有 input cascode(M4,M5)相当于,M1,M2的drain端接了一个大电阻(小信号);会产生严重的miller效应;降低电路速度,引入大极点。
实际从输入输出传递函数上这个大极点是不存在的,这样分析无意义。
我说了,这个是在假定前级信号源是有内阻的,这个input cascode就是希望,M1,M2的drain端看到小电阻。减小输入端的miller效应
使用这种结构一般是M1,和M2管非常大。用这种结构后从M4,M5的源级看进去的阻抗一定是1/gm而不是ro(虽然M4 M5漏端看到主抗约ro/2)?
有点道理;
这两个管子还可以1)提高增益;2)减小M6,7Drain端的寄生;3)在给定Ibias的条件下,可以相应的减小输入管的L以优化噪声,同时不会明显降低增益;
当然,牺牲了一些共模输入范围。
严格分析从M1,M2drain看到的电阻大小应为:(0.5ro+ro)/(1+gm*ro)=1.5/gm。总之,比不加M4,M5要小很多了。
这跟triple cascode 有区别么?
这种结构,提高不了增益,增益还是gmro的平方;你讲的tripple,增益是gmro的立方
小编是否可以看一下拉闸为249页,推倒该点阻抗时,电流并不流过恒流源负载,因此从输入输出考虑该点阻抗并非高阻。
久不看razavi了,谢谢你,刚才找师兄的书要看,发现razavi果然又在乱写了。 razavi的写法,是基于cascode管子的drain端是小电阻的情况,很明显这是他用错了公式导致的。
因为razavi在书中200多页这样写道这个点是低阻,所以这个点是低阻?
razavi的那本射频微电子还是有点看头的,但是analog那本书还是算了; sansen和gray才是可以仔细研究的。
现在我也不推荐看书了,书上内容过时的多,多看国外录像,课外课件,完成国外project,国外作业,比拿一本书看,要进步快得多的多。
(P.S. 喜欢搞软件的,快去搞软件啊,昨天上课,我老师又在喷微电子行业现状了,江河日下啊!我们问他:那怎么半,前途呢?他说:“去越南,这种三流国家还是需要你们这些工程师的;印度不要去,喝口水都会中毒”)
小编大牛。这么说拉闸为阿。我觉得是不是两种可能。1、拉闸为确实忽视了恒流源负载的大阻抗得到这个1/gm得结论;2、他认为推倒这点阻抗时忽视大的恒流源阻抗时有道理的所以得到了他书上的结论。
我不是大牛,但我经常喷razavi的,熟悉我的人都知道。
p.s. 这个东西,我们用手推一下不行么? 手算能力呢? 推倒一下,你就发现结果了啊
sansen书上152页,他也说这点阻抗是1/gm
你要想驳我的结论,你得拿出真正的道理啊,不是sansen说什么,razavi说什么就是什么啊;他们有时这样说是基于某种语境,比如想简化分析;但是,在这个题中,明显不能做这种简化了啊。
他们这样说,他们说错了。
你把输出端直接接地,才会有你的结论
这个结论我推过,但在不一样的前提下推出来结论是不一样的。我的理解是输入电流直接流到负载电容,恒流源负载的阻抗并没有参与小信号电流的传递,因此他的阻抗不应该计算进去。
折叠点阻抗高的原因是 因为M8,9drain端向下看的阻抗很大。在分析电阻的时候,是基于低频,不考虑电容的。
即使照你说的,你的结论也不会是1/gm,你要把sCL也考虑的(虽然,这种思路完全错误)。
我说的恒流源就是指下面的4个管子,cascode恒流源。他阻抗是很大,因此电流恒定,所以输入小信号电流不会从这上面走,都是流到负载电容上去了。从小信号电流的流向即输入输出的关系上来说,那个大的恒流源阻抗不会导致折叠点成为一个高阻。
再者。如果折叠点阻抗真的是高阻,意味着这点电压变化将很大,但实际上这点被vgs钳位,不可能变化很大。如果变化大,必然要从负载电容上输出或吸入电流。因此这点不会是高阻。
你说的totally 错误,你应该仔细复习一下,求电阻的方法; 电容的阻抗在低频下是无穷大的好吗
我觉得你这条说法,表明你很多基本概念都是错误的,你应该加强基础复习,如果你想从事analog的话(虽然没什么钱)。
小信号电阻推倒是学模拟的基本功,这个自然不用说。但推之前对问题的理解也很重要,理解错了自然推出来错的结果。
所以,谁理解错了?
算了下,M1,M2drain看到的电阻差不多是1/gm 级别的阻抗。共栅极输入阻抗只有在共栅极漏端的电流源阻抗远大于ro(如ro*gmro)时,才不能看作是1/gm 级别的。
回小编,我只是一刚参加工作的做模拟的,但自认为学的还算严谨扎实。我觉得拉闸为和sansen既然观点一致一定是有道理的,他们不会想不到这个简单的问题,不敢轻易反驳。所以我认为小编你可能错了。
你觉得软件挣钱不累么?
恩,是这样的
诶,你的问题,在于太相信书了;你要自己推导一下啊,然后,你的一些基本物理概念都是模糊的,希望你加油!
小编你推到的该点到地的阻抗确实是高阻没错,但你没有想到输出点的位置的影响。从输入输出路径上来看,这点不会是高阻,因此传递函数、次极点表达式中,不会显示这点是高阻。
