运放的THD+N和位数

对于运放的THD+N和位数该如何理解理解（有效位数ENOB=（SINAD-1.76）/6.02）

Definition

An often used definition for ENOB is

,

where all values are given in dB, and

• SINAD is the ratio indicating the quality of the signal
• The 6.02 term in the divisor converts decibels (a log₁₀ representation) to bits (a log₂ representation)
• The 1.76 term comes from quantization error in an ideal ADC

This definition compares the SINAD of an ideal ADC or DAC with a word length of ENOB bits with the SINAD of the ADC or DAC being tested.

1.76是数字系统量化误差损失的动态范围。6.02是 (log10 / log2)，用于将dB转换为bit数。

两者的关系

THD+N 和 SINAD的关系是 ：SINAD = 20* log (1/(THD+N)) 

以OPA350为例，LOW THD+NOISE: 0.0006%

那么，SINAD则为104dB。

书上讲算出的精度不是它的直流精度，而是指它的交流特性，那么请问这个精度究竟如何理解呢，也就是说这个精度有何意义？

楼主能否把你的参考资料共享一下？需要更多前后文来分析上面的说法。

或者这样理解，THD+N对于运放本身并不是一个恒定的值，只是一个典型值（点击图片看大图）

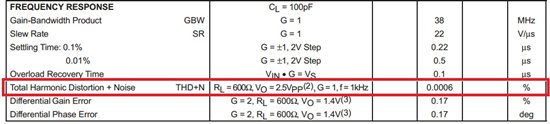
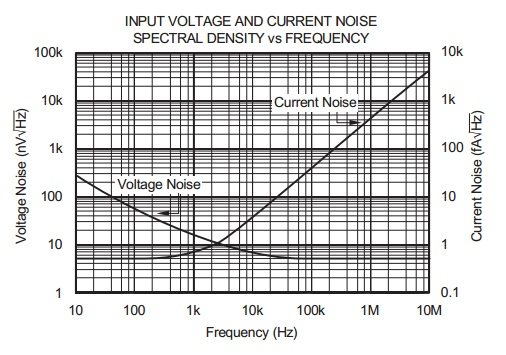
在接近DC段，voltage noise会增大，这就是1/f noise。因此我们通过THD+N计算出来的SINAD也是一个典型值。

德州仪器高性能单片机和模拟器件在高校中的应用和选型指南  黄争编  76页

贴出原文，原文的计算方法和上面提到的计算方法是一致的。

同理对于OPA350，(20*log(1/0.000006)-1.76)/6.02 = 17bit。关于交直流的精度差异，楼主可以参考上面的解释。

请问算出运放的ENOB有什么意义呢？

这样能够帮助我们为ADC DAC 选择合适的运算放大器。充分利用整个信号系统中的动态范围。

运放的噪声跟带宽有关。对于很窄的带宽，噪音很低。但随着带宽的增加，噪声随之增加。难道位数随带宽变化也变化？

@Frank   THD+N是个典型值，所以，实际上的位数与带宽有关系。准确的说，带宽窄，噪声功率小，噪声的单位是 nV/((hz)^0.5)。