找了篇讲A/D噪声性能方面的资料,大家看下(1)
所有模数转换器(ADC)都有一定数量折合到输入端的噪声,通常被看作一种与无噪声ADC的输入端串联的噪声源。不应该把折合到输入端的噪声与量化噪声相混淆,量化噪声仅在ADC处理随时间变化的信号时有意义。在大多数情况下,输入噪声越小越好;但是在有些情况下,输入噪声实际上对提高分辨率是有帮助的。
折合到输入端的噪声(编码跃迁噪声)
实际的ADC在许多方面与理想的ADC有偏差。折合到输入端的噪声(又称作有效输入噪声)无疑是偏离理想值,它对ADC总传递函数的影响如图1所示。当模拟输入电压增加时,“理想的”ADC(如图1(a)所示)保持一个恒定的输出编码直到达到一个跃迁区,在那一点上输出编码立刻跳变到下一个量化值,并且一直保持到达到下一个跃迁区域。理想的ADC具有零编码跃迁噪声,并且跃迁区域的宽度为零。实际的ADC有一定数量的编码跃迁噪声,因而具有有限的跃迁区域宽度。图1(b)示出编码跃迁噪声宽度约为一个最低有效位(LSB)峰峰值(P-P)噪声的情况。

图1 编码跃迁噪声及其对ADC传递函数的影响
从内部结构来看,所有ADC电路都会由于电阻器噪声和“kT/C”噪声而产生一定数量的有效值(RMS)噪声。这种噪声甚至对于直流输入信号也会出现,被认为是造成编码跃迁噪声的原因,现在通常称作折合到输入端的噪声。折合到输入端的噪声最常用的表征方法是检查大量输出采样的直方图,同时ADC的输入端保持在一个恒定的直流值。最高速或最高分辨率ADC的输出是编码的分布,通常集中在直流输入标称值的周围,如图2所示。
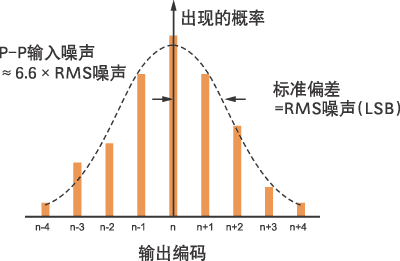
图2 折合到输入端的噪声对ADC的输入接地直方图的影响
为了测量折合到输入端的噪声的数量,要将ADC的输入端接地或连接到一个深度去耦的电压源,然后采集大量的输出采样,并且将其绘制为直方图(如果ADC的输入标称值为0V,则称之为输入接地直方图)。由于该噪声是近似的高斯(Gaussian)分布,所以该直方图的标准偏差σ可以计算,它相当于RMS输入噪声。通常的做法是用LSB的RMS来表示这种RMS噪声,相当于折合成ADC满度输入范围的RMS电压。如果模拟输入范围以数字量或个数来表示,那么输入值(例如,σ)可以用LSB的数量来表示。
尽管ADC内在的微分线性误差(DNL)会造成与理想的高斯分布的偏差(例如,图2中有一些DNL是很明显的),但应当至少近似于高斯分布。如果有显著的DNL偏差,那么应对于几个不同的DC输入电压进行平均计算σ值。如果编码分布明显是非高斯分布的,例如有大而明显的波峰或波谷,这就表明对ADC设计得不好,或很可能是印制板布线不好,接地设计差,或电源去耦不正确,图3中的输入接地直方图表明存在这些设计缺陷。出现麻烦的另一个迹象是,当ADC的直流输入超过ADC的输入电压范围时使高斯分布的宽度剧烈变化。
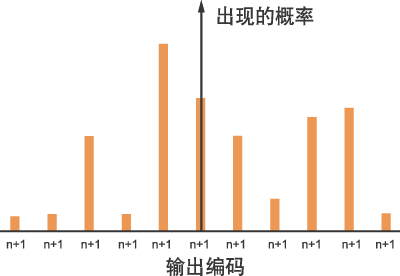
图3 存在设计缺陷时的输入接地直方图
无噪声码分辨率
ADC的无噪声码分辨率是指超过这个位(bit)数它就不能清楚分辨个别编码的分辨率。这种限制是由于上文所述与所有ADC相关的有效输入噪声(或折合到输入端的噪声),通常表示为一个以LSB rms为单位的RMS值。RMS噪声乘以因数6.6,转换为有用的P-P噪声(可表示编码的实际不确定性),表示为LSB P-P。
由于一个N位ADC的总转换编码数是2N LSB,因此总的无噪声码数量等于:
(1)
![]()
无噪声编码数量可通过计算以2为底的对数转换为无噪声(二进制)码分辨率,用公式2表示。
(2)
![]()
无噪声码分辨率指标一般与高分辨率Σ-ΔADC有关,它通常是采样速率、数字滤波器带宽和可编程增益放大器(PGA)增益(因此关系到输入范围)的函数。表1示出默认加电方式下,典型的无噪声码分辨率表,取自Σ-ΔADCAD7730的产品技术资料1。该表表明P-P分辨率与输入范围和更新速率(CHP=1)的关系,括号内是P-P分辨率的位数。

表1 AD7730Σ-ΔADC的无噪声码分辨率
应当注意的是,对于50Hz输出数据速率和610mV输入范围的Σ-ΔADC,其无噪声码分辨率是16.5bit(80,000个无噪声编码)。在这些条件下的建立时间为460ms,从而使得这种ADC非常适合用于精密电子秤应用。这种数据可以从许多适合精密测量应用的高分辨率Σ-ΔADC的产品技术资料中获得。
满度范围与RMS输入噪声(而不是P-P噪声)的比率有时用于计算分辨率。在这种情况下,采用术语有效分辨率。应当注意,在相同条件下,有效分辨率比无噪声码分辨率大log2(6.6),约为2.7bit。
(3)
![]()
有效分辨率=无噪声码分辨率+2.7bit (4)
一些制造商喜欢采用有效分辨率而不是无噪声码分辨率,因为那样bit数较高,用户应当仔细检查产品技术资料以确认实际上采用的是哪种分辨率定义。
数字平均提高分辨率和减少噪声
通过数字平均可以减少折合到输入端的噪声的影响。考虑一个16bit ADC,它以100kSPS采样速率工作,具有15bit无噪声码分辨率。对一个同样信号的每次输出采样做两次测量结果平均,使有效采样速率减少到50kSPS,信噪比(SNR)提高3dB,并且无噪声码分辨率提高到15.5bit。如果对每次输出采样做四次测量平均,采样速率减少到25kSPS,SNR提高6dB,并且无噪声码分辨率提高到16bit。
甚至可以进一步对每次输出采样做16次测量的平均,输出采样速率减少到6.25kSPS,SNR再增加6dB,无噪声码分辨率增加到17bit。为了明显提高“分辨率”,必须实行多次精密平均。
平均过程也有助于平滑ADC传递函数的DNL误差。这可以通过ADC在量化编码k上有失码的简单情况来举例说明。尽管编码k由于大的DNL误差而丢码,但两个相邻编码k-1和k+1的平均值仍等于k。
因此这种方法以牺牲总体输出采样速率和增加数字硬件为代价,有效地用来增加ADC的动态范围。还应当注意的是,平均过程不会修正ADC内在的积分线性误差(INL)。
现在,考虑一个具有极低折合到输入端的噪声的ADC的情况,无论进行多少采样,其直方图都示出一个单个编码。对于这个ADC,数字平均会起什么作用?答案很简单——没有作用!无论对多少采样进行平均,结果都一样。但是,一旦有足够大的噪声施加到输入信号,就会有多于一个的编码出现在直方图中,平均方法又开始起作用。因而很有意思,有些少量的噪声是好噪声(至少对于平均方法而言);但是,出现在输入端的噪声越多,就需要越多的平均以达到同样的分辨率。
不要混淆有效位数(ENOB)和有效分辨率或无噪声码分辨率
由于术语的相似性,有效位数和有效分辨率经常被以为是相同的,但实际情况并不是这样。
有效位数(ENOB)是当用一个满度正弦波输入信号激励ADC时,对其输出的快速傅里叶变换(FFT)分析所产生的。计算所有噪声和失真项的平方和的平方根(RSS)值,可定义信号对噪声加失真的比率,称作信噪失真比(S/(N+D))或信纳比(SINAD)。一个理想的N bit ADC的理论SNR由以下公式给出:
SNR=6.02N+1.76dB (5)
通过将公式5中的SNR用计算出的ADC的SINAD代替并且对N进行求解,可以计算出ENOB。
(6)
![]()
用于计算SINAD和ENOB的噪声和失真不仅包括折合到输入端的噪声,而且包括量化噪声和失真项。SINAD和ENOB用于测量ADC的动态性能,而有效分辨率和无噪声码分辨率用于衡量在直流输入条件下ADC的噪声,在直流输入条件下量化噪声不是一个问题。
