泰勒离散线源综合-matlab实现

function I = taylor_line(N, SLL)
M = 10000;
d = 1/2;
L = (N)*d;% antenna length
   theta = 0:pi/M:pi;%
%  theta = linspace(-pi/2,pi/2,M+1)
x = L*cos(theta);
f0 = 1e9;
%lambda = 3e8/f0;
%d = lambda/2;% elements spacing
k =2*pi;% wave constant
R = 20; % amplitude ration between mainbeam and sidelobe , dB
A = acosh(10^(-SLL/20))/pi;
% T = cos(pi*sqrt(x.^2-A^2));
% af = 20*log10(abs(T)/max(T));
% error = 0.001;
% % af=U;
% pos1_3dB = [];
% pos_max = find(max(af)==af);
% while(isempty(pos1_3dB))
%     pos1_3dB = find(abs(((af(1:pos_max)-af(pos_max)))+3) < error);
%     error = error + 0.001;
% end
% error = 0.001;
% pos2_3dB = [];
% while(isempty(pos2_3dB))
%     pos2_3dB = find(abs(((af(pos_max:end)-af(pos_max)))+3) < error);
%     error = error + 0.001;
% end
% BeamWidth= (theta(pos2_3dB(1)+pos_max)-theta(pos1_3dB(end)))/pi*180;
% figure;
% plot(theta,af);
% hold on;
% str = strcat('L=', num2str(L),'\lambda, SLL = -',num2str(R) ,'dB ');
% bw = strcat('mainbeam beamwidth=',num2str(BeamWidth),'degree ');
% text(pi*2/3,-5,str,'fontsize',12);
% text(pi*2/3,-8,bw,'fontsize',12);
% title('Radiation Pattern of an Idealized Equvialent Sidelobe Array ');
% xlabel('Phase');
% ylabel('Amplitude');
% ylim([-60 0]);
%%
% Taylor synthesis
% theta = -pi/2:0.01:pi/2;%
% x = L*cos(theta);
n1 =ceil(A^2*2+0.5);% the first 3 sidelobes have almost same amplitude
%   n1 =4;
%I=taylorwin(N,n1,SLL);
sigma = n1/sqrt(A^2+(n1-0.5)^2);
xn = zeros(1,n1-1);
for j = 1:1:n1-1
xn(j) = sigma*sqrt(A^2+(j-0.5)^2);
%  xn(j) = j*sqrt(A^2+(j-0.5).^2)/sqrt(A^2+(n1-0.5).^2);
end
for i = 1:1:length(x)
    if x(i) = 0
        T(i) = sin(pi*x(i))/pi/x(i)*cosh(pi*A);
        for j = 1:1:n1-1
        T(i) = T(i)*(1-(x(i)/xn(j))^2)/(1-(x(i)/j)^2);
        end
    else
        T(i) = cosh(pi*A);
        for j = 1:1:n1-1
        T(i) = T(i)*(1-(x(i)/xn(j))^2)/(1-(x(i)/j)^2);
        end
    end
end
T = T / max(T);
I =ones(1,N);
% zn = zeros(1,N);
for i = 1:1:N
     if mod(N,2) == 1
        zn = abs((i-(N+1)/2)*d*2/L);
     else
        %#zn = (i-(N+1)/2)*d
        if i < (N+1)/2
            zn = (2*abs((N/2+1)-i)-1)*d/L;
        else
            zn = (2*abs(i-N/2)-1)*d/L;
        end
     end
    for j = 1:1:n1-1
%          I(i) = I(i) + 2*T((find( min(abs(x-j))==abs(x-j))))*cos(j*pi*zn);
          tmp = power(prod(1:(n1-1)),2)/prod(1:(n1-1+j))/prod(1:(n1-1-j));
        for k = 1:1:n1-1
            tmp = tmp* (1-j^2/sigma^2/(A^2+(k-0.5)^2));
        end
          
          I(i) = I(i) + 2*tmp*cos(j*pi*zn);
    end
end
I = I/max(I);
end
对于N=10，SLL=-30,综合结果如下：

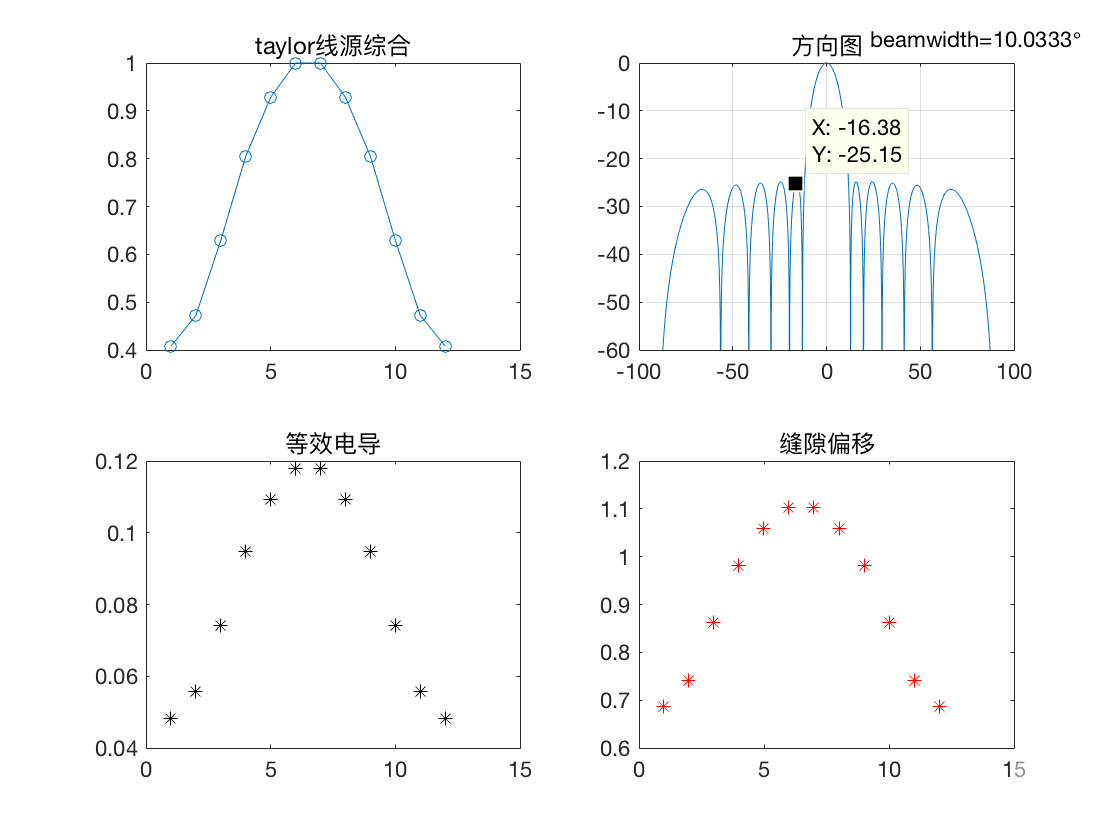
没有注释吗?