天线功率叠加有个悖论,能解释一下吗?
两个天线只馈入了2W的功率,怎么辐射了4W ?详情见下图:
困扰了很久。感觉这是个悖论,应该怎么解释?
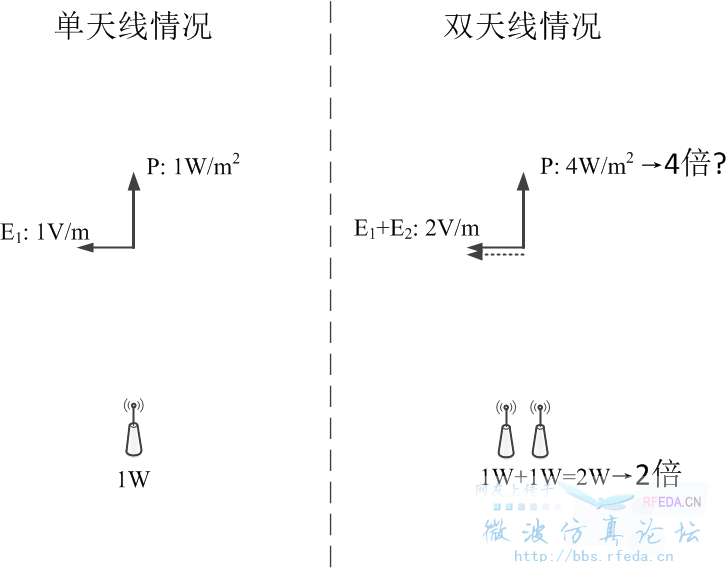
我也不是很明白。和你讨论下。
辐射场按场叠加原理,空间各处场强变为2倍。
但是场强 的单位不是W/m2,你写的是V/m2,这个过程是不是经过转化了,是不是应该直接是功率相加后再算电压,而不是电压相加后反算功率。
纯属讨论。错误勿怪
关于场与功率的关系大致如1楼所言,小编还有个地方可能要注意,有的是功率密度单位表示,有的是功率单位表示,这里面存在着能量分布的问题,所以才有增益这个概念的引入。
单天线和双天线肯定不一样
两个天线都输入1W的功率,的确可以提高增益6dB,比单天线多输入一倍功率的3dB肯定要好
但是那是两个天线正常工作并叠加的结果,但是两个天线靠那么近肯定不能正常工作
天线阵列就是这么回事,先功率分成n份,单个天线是1/n,再远场电厂叠加是n^2,,再相乘就是n倍
其实就一点需要注意,电压(场强)换成功率的时候请考虑负载阻抗,一个天线的时候是50ohm,两个天线的时候是两个50ohm
小编考虑过两个天线相位相反的情况吗?
两个50欧姆的并联还是串联?
他既然想把场强直接加成2倍,我猜他的应用场景里估计该是串联。
具体考虑当然还有相位等因数了,他这个例子的错就错在场强叠加了,可是没有叠加相应的阻值
既然要考虑两个天线放在一起形成的总场,就意味着电磁场在远场形成了干涉,从而导致每一个天线单独放置时的原始场分布发生了改变,天线的输入阻抗也会随之改变(即使希望他们是相互隔离的),这是解释该矛盾的核心。
如果两个天线隔得足够远,他们的输入阻抗会影响得这么大么?而与此同时,假设其在远处某点也是同相叠加的。那这个问题该如何解释呢?
还是说由于在某些点是同相叠加的,某些点是反相抵消的,所以总的效果会保证积分出来功率守恒?
@tensor ,有bug:写到一半的东西全丢了……只因为我手欠,点了一下本页面别的地方
说回正题:我理解你说的“隔得足够远”是比波长大很多,比如10个波长。这种情况下,干涉仍然存在,但每个天线单元的输入阻抗和独立工作时相差不多;确实如你所说,有些方向同相叠加,有些方向反相相消,计算总的辐射功率时会发现功率守恒。
确实只考虑了同相叠加的情况。反相的话处处相消,辐射场处处为0。
如果它们的相差为90°,好像总功率就等于2W了。
难道两个天线靠得很近会产生相差?
但是如果所有条件都对称,天线2 使 天线1的相位滞后45°,那天线1同样使天线2滞后45°,两个不就又没有相差了吗?
想了很长时间觉得是天线近距离耦合的问题,两个天线各馈1W后,辐射电流不是叠加成2倍了,而是由于耦合变成了√2倍,即等效于单天线馈入2W功率的情况。只是猜想,怎么证明?
不知道有没有更好、更让人信服的解释!
这个悖论几年前在我们这就有过激烈的争论,焦点只有两个,第一必须遵守能量守恒,第二必须遵守矢量叠加,这两个必须同时满足
解决这个“悖论”的关键就是理解场的空间分布,首先必须肯定适量叠加原理的正确性,当电压增加一倍时功率增加四倍,这也是相控阵雷达上增加单元数的效果比增加单个单元功率的实现的雷达威力大的原因;同时必须理解这个增加的额外的功率并不是源提供的,而是空间“搬移”过来的,也就是说在A点增加的额外功率是由B点“搬移”过来的。
这样说能理解么?
如果是空间搬移的话那总功率应该守恒才对。
但是两个源距离小于 λ/2 的时候各处叠加会导致功率大于原来两倍。
距离再大时,总功率为原来2倍也只是近似成立。
百度文库里找到一篇《波叠加时的能量佯谬》,跟大家分享,继续讨论。
http://wenku.baidu.com/view/35f49837f111f18583d05a48.html
这是赵老师写的啊
以前学光学学得头皮发麻啊
这个应该可以按照电磁波的干涉和叠加原理来解释!
天线摆放的位置距离都会影响叠加后的场型,能量守恒定律一定是正确的,不可能像你说的再任何方向都是加强的,也可能是相互抵消的,并且加强的场型也会变得有指向性
你可以对园面积分求总辐射功率
很困扰的问题,期待有人仿真一下,
