信道编码的发展史
时间:10-02
整理:3721RD
点击:
信道编码,也叫差错控制编码,是所有现代通信系统的基石。几十年来,信道编码技术不断逼近香农极限,波澜壮阔般推动着人类通信迈过一个又一个顶峰。5G到来,我们还能突破自我,再创通信奇迹吗?
所谓信道编码,就是在发送端对原数据添加冗余信息,这些冗余信息是和原数据相关的,再在接收端根据这种相关性来检测和纠正传输过程产生的差错。
这些加入的冗余信息就是纠错码,用它来对抗传输过程的干扰。
1948年,现代信息论的奠基人香农发表了《通信的数学理论》,标志着信息与编码理论这一学科的创立。根据香农定理,要想在一个带宽确定而存在噪声的信道里可靠地传送信号,无非有两种途径:加大信噪比或在信号编码中加入附加的纠错码。
这就像在嘈杂的酒吧里,酒喝完了,你还想来一打,要想让服务员听到,你就得提高嗓门(信噪比),反复吆喝(附加的冗余信号)。
但是,香农虽然指出了可以通过差错控制码在信息传输速率不大于信道容量的前提下实现可靠通信,但却没有给出具体实现差错控制编码的方法。
人类在信道编码上的第一次突破发生在1949年。
R.Hamming和M.Golay提出了第一个实用的差错控制编码方案。
受雇于贝尔实验室的数学家R.Hamming将输入数据每4个比特分为一组,然后通过计算这些信息比特的线性组合来得到3个校验比特,然后将得到的7个比特送入计算机。
计算机按照一定的原则读取这些码字,通过采用一定的算法,不仅能够检测到是否有错误发生,同时还可以找到发生单个比特错误的比特的位置,该码可以纠正7个比特中所发生的单个比特错误。这个编码方法就是分组码的基本思想,Hamming提出的编码方案后来被命名为汉明码。
汉明码的编码效率比较低,它每4个比特编码就需要3个比特的冗余校验比特。另外,在一个码组中只能纠正单个的比特错误。
M.Golay先生研究了汉明码的缺点,提出了Golay码。
Golay码分为二元Golay码和三元Golay码,前者将信息比特每12个分为一组,编码生成11个冗余校验比特,相应的译码算法可以纠正3个错误;后者的操作对象是三元而非二元数字,三元Golay码将每6个三元符号分为一组,编码生成5个冗余校验三元符号,这样由11个三元符号组成的三元Golay码码字可以纠正2个错误。
Golay码曾应用于NASA的旅行者1号(Voyager 1),将成百张木星和土星的彩色照片带回地球。
在接下来的10年里,无线通信性能简直是跳跃式的发展,这主要归功于卷积码的发明。
卷积码是Elias在1955年提出的。
卷积码与分组码的不同在于:它充分利用了各个信息块之间的相关性。
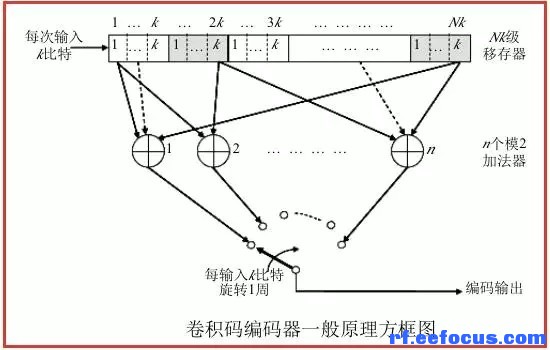
通常卷积码记为(n,k,N)码。卷积码的编码过程是连续进行的,依次连续将每k个信息元输入编码器,得到n个码元,得到的码元中的检验元不仅与本码的信息元有关,还与以前时刻输入到编码器的信息元(反映在编码寄存器的内容上)有关。同样,在卷积码的译码过程中,不仅要从本码中提取译码信息,还要充分利用以前和以后时刻收到的码组。从这些码组中提取译码相关信息,而且译码也是可以连续进行的,这样可以保证卷积码的译码延时相对比较小。通常,在系统条件相同的条件下,在达到相同译码性能时,卷积码的信息块长度和码字长度都要比分组码的信息块长度和码字长度小,相应译码复杂性也小一些。
很明显,在不到10年的时间里,通信编码技术的发展是飞跃式的,直到遇到了瓶颈。
根据香农前辈的指示,要提高信号编码效率达到信道容量,就要使编码的分段尽可能加长而且使信息的编码尽可能随机。但是,这带来的困难是计算机科学里经常碰到的“计算复杂性”问题。
还好,这个世界有一个神奇的摩尔定律。
得益于摩尔定律,编码技术在一定程度上解决了计算复杂性和功耗问题。而随着摩尔定律而来的是,1967年,Viterbi提出了Viterbi译码算法。
在Viterbi译码算法提出之后,卷积码在通信系统中得到了极为广泛的应用,如GSM、 IS-95 CDMA、3G、商业卫星通信系统等。
但是,计算复杂性依然是一道迈不过的墙。
尽管人们后来在分组码、卷积码等基本编码方法的基础上提出了许多简化译码复杂性的方法,但是均因无比高耸的计算复杂性之墙阻挡而变得不可逾越。
编码专家们苦苦思索,试图在可接受的计算复杂性条件下设计编码和算法,以提高效率,但其增益与香农理论极限始终都存在2~3dB的差距。
直到1993年,在日内瓦召开的 IEEE通信国际会议上,两位当时名不见经传的法国电机工程师C.Berrou和A.Glavieux声称他们发明了一种编码方法,可以使信道编码效率接近香农极限。
这一消息太“轰动”了,因为几乎所有的专家都认为这俩“棒槌”是来捣乱的。
这么多数学家都没能突破,就你这两个小角色也敢宣称接近香农极限?不是存心捣乱吗?一定是计算上出了错误吧?
许多专家甚至懒得去读完这篇论文。
事实上,这两位法国老兄的数学功底可能真的不怎么样,他们没有试图从数学上找突破口,因此他们的论文在会上被怀疑和忽略就不足为奇了。
但是,专家们忽略了一个问题。凭着电机工程师的经验,他们发现在电子学中经常用到的反馈概念似乎被数学家们忽略。也许反馈能够使我们绕过计算复杂性问题,于是他们就设计了一套新的办法。
首先他们摈弃了“纯粹”的数字化概念。在典型的数字化方法中,总是先把某一电平设定为阈值。信号电平高于这一阈值就判决为“1”,低于就判决为“0”。在Turbo码解码过程中,某一特定比特的电平被量化为整数,例如从-127到+127。其数值就作为判决该比特为“1”或“0”的可置信度的度量(例如-110意味该比特非常非常可能是“0”,而+40 意味该比特也许是“1”但把握不大)。
其次,与其他系统不同,Turbo码系统在发射端和接收端分别设置两个编码器和解码器。其中一对编解码器对特定的一段比特流进行奇偶校验码的加入和校验计算,另一对编解码器则在同一段码流经过交织扰动后对其进行上述同样操作。
▲Turbo编码器结构。Turbo码编码器是由两个或多个反馈的系统卷积码编码器通过一个随机交织器并行连接而成,编码后的校验位经过删余矩阵,从而产生不同码率的码字。
由于这两段码流包含同样的数据,如果没有信道噪声,解码结果应该一致。但在噪声干扰下两组结果会产生差别。通过上述对比特判决的可置信度信息的帮助,把这两组结果彼此参照,可以得出第一次近似的结果。把这一结果“反馈”到解码器前端,再进行迭代,经过几次迭代两个解码器的结果就会互相接近(收敛)。这样就绕过了计算复杂性问题。
▲Turbo码的译码器有两个分量码译码器,译码在两个分量译码器之间进行迭代译码,故整个译码过程类似涡轮(turbo)工作,所以又形象的称为Turbo码。
当然这样做也得付出代价。由于迭代解码,必然会产生时延。所以对于实时性要求很高的场合,Turbo码直接应用会受到限制。
接下来,那些编码专家们跌破了眼镜。不可思议,当其他小组验证了这两位法国老兄的方案时,证明了结论是正确的。现在人们谈论的已经是和香农极限相差0.1dB还是0.01dB了。
一个通信编码史上的革命性的时代到来了!两位名不见经传的电机工程师不顾科学权威认定的种种“极限”,在一片嘲笑声中,另辟蹊径,突破了理论壁垒。
一开始,Turbo码只是应用于一些特殊场合,比如卫星链路。后来,研究人员将它扩展到数字音频和视频广播领域。
紧接着,Turbo码成为通信研究的前沿,全世界各大公司都聚焦在这个领域,包括法国电信、NTT、DoCoMo、索尼、NEC、朗讯、三星、爱立信、诺基亚 、 摩托罗拉和高通等等。
Turbo码成为了始于本世纪初的3G/4G移动通信技术的核心,直到今天4.5G,我们依然在采用。
现在,编码专家们都松了一口气,总算解决了这个棘手的问题。也同时都叹了一口气,因为这已经接近香农极限了,发现似乎在这领域已经很难再突破了。
收工,回家,带娃。
但是,在1999年,编码界又发生了一件有趣的事。人们重燃起了对LDPC的兴趣,尽管它已经被人们遗忘了几十年。
LDPC( low-density parity check),即低密度奇偶校验码。它于1962年由Gallager提出,然后,被人们遗忘了。直到Turbo码被提出以后,人们才发现Turbo码从某种角度上说也是一种LDPC码。
另一件让人们感兴趣的事是,LDPC码发明较早,其基本专利到1999年就到期了,而Turbo码要到2013年才到期。
LDPC利用校验矩阵的稀疏性,使得译码复杂度只与码长成线性关系,在长码长的情况下仍然可以有效的进行译码,因而具有更简单的译码算法。随着人们对 LDPC码重新进行了研究,发现LDPC 码与Turbo一样具有逼近香农极限的性能。较新的研究结果显示,实验中已找到的最好LDPC码,其极限性能距香农理论限仅相差0.0045dB。
接着,LDPC在IEEE 802.11n 以及802.16的技术提案中被热烈讨论。DVB-S2也决议以LDPC替代Turbo码。有人认为,LDPC是终极纠错编码,极有可能成为未来主流编码技术。
所以,一场关于Turbo码和LDPC码的争论就拉开了。随着5G标准化的到来,Turbo码和LDPC码像拳击台上两名重量级选手,两人都宣称自己将是获胜者,但裁判的结束哨声却一直未吹响。
裁判很头痛,这是一场几乎无法打分的比赛。因为,之所以有争论,无非是要证明,谁才更适合未来5G用例?谁才能更好满足新的技术需求?
众所周知,2G的应用场景是语音和低速率数据业务,3G和4G的应用场景是语音和更高速率的数据业务。可以确定的是,Turbo码和LDPC码都能很好的满足3/4G,甚至是4.5G用例。
而5G用例呢?市场上还没有出现,而且很多。不管是Turbo码,还是LDPC码,都无法确定谁才是最好的选择。而且,由于两者各有优缺点,要覆盖全部5G应用,不太现实。
正当Turbo码和LDPC码打拳击赛之时,Polar码冲上了拳台,变成了一场摔角运动。
很幸运,在编码技术不断打破记录带给我们惊喜时,另一项编码领域里的激动人心的研究已浮出水面。
2007年,土耳其比尔肯大学教授E. Arikan基于信道极化理论提出的一种线性信道编码方法,即Polar码。该码字是迄今发现的唯一一类能够达到香农限的编码方法,并且具有较低的编译码复杂度,当编码长度为N时,复杂度大小为O(NlogN)。
Polar码的理论基础就是信道极化。信道极化包括信道组合和信道分解部分。当组合信道的数目趋于无穷大时,则会出现极化现象:一部分信道将趋于无噪信道,另外一部分则趋于全噪信道,这种现象就是信道极化现象。无噪信道的传输速率将会达到信道容量I(W),而全噪信道的传输速率趋于零。Polar码的编码策略正是应用了这种现象的特性,利用无噪信道传输用户有用的信息,全噪信道传输约定的信息或者不传信息。
这就像一个班上的同学,上学时间足够长的话,差的学生大部分会跌到谷底,好的学生大部分会飞向云巅,然后,抛弃那些学渣…
Polar码比Turbo码和LDPC码更接近信道容量,Polar码可以保证5G任何场景的高性能通信。夸张的讲,如果不考虑系统设计问题,编码技术的历史就应该到此终结了,终结在Polar码的手里。
但是,编解码的复杂性是Polar的问题,不过,在使用改进后的SCL(Successive Cancelation List)译码算法时能以较低复杂度的代价,接近最大似然译码的性能。
关键是,Polar码还是太年轻了,发明得比较晚,很多研究还建立在理论基础上,不像Turbo码和LDPC码已经广泛应用于实际场景。只有等待时间来告诉我们,Polar码到底是不是5G信道编码的王者。
回顾信道编码历史,波澜壮阔。在几十年并不漫长的岁月里,一次又一次关键技术的历史性突破,造就了今天人类通信奇迹。而当5G即将到来之时,更令人兴奋的是,我们看到了各种优秀的编码技术的涌现。毫不夸张的说,这是信道编码技术的文艺复兴时期。而开启文艺复兴之门的,不仅仅是信道编码,5G将激发无线产业史无前例的创新活力。
所谓信道编码,就是在发送端对原数据添加冗余信息,这些冗余信息是和原数据相关的,再在接收端根据这种相关性来检测和纠正传输过程产生的差错。
这些加入的冗余信息就是纠错码,用它来对抗传输过程的干扰。
1948年,现代信息论的奠基人香农发表了《通信的数学理论》,标志着信息与编码理论这一学科的创立。根据香农定理,要想在一个带宽确定而存在噪声的信道里可靠地传送信号,无非有两种途径:加大信噪比或在信号编码中加入附加的纠错码。
这就像在嘈杂的酒吧里,酒喝完了,你还想来一打,要想让服务员听到,你就得提高嗓门(信噪比),反复吆喝(附加的冗余信号)。
但是,香农虽然指出了可以通过差错控制码在信息传输速率不大于信道容量的前提下实现可靠通信,但却没有给出具体实现差错控制编码的方法。
人类在信道编码上的第一次突破发生在1949年。
R.Hamming和M.Golay提出了第一个实用的差错控制编码方案。
受雇于贝尔实验室的数学家R.Hamming将输入数据每4个比特分为一组,然后通过计算这些信息比特的线性组合来得到3个校验比特,然后将得到的7个比特送入计算机。
计算机按照一定的原则读取这些码字,通过采用一定的算法,不仅能够检测到是否有错误发生,同时还可以找到发生单个比特错误的比特的位置,该码可以纠正7个比特中所发生的单个比特错误。这个编码方法就是分组码的基本思想,Hamming提出的编码方案后来被命名为汉明码。
汉明码的编码效率比较低,它每4个比特编码就需要3个比特的冗余校验比特。另外,在一个码组中只能纠正单个的比特错误。
M.Golay先生研究了汉明码的缺点,提出了Golay码。
Golay码分为二元Golay码和三元Golay码,前者将信息比特每12个分为一组,编码生成11个冗余校验比特,相应的译码算法可以纠正3个错误;后者的操作对象是三元而非二元数字,三元Golay码将每6个三元符号分为一组,编码生成5个冗余校验三元符号,这样由11个三元符号组成的三元Golay码码字可以纠正2个错误。
Golay码曾应用于NASA的旅行者1号(Voyager 1),将成百张木星和土星的彩色照片带回地球。
在接下来的10年里,无线通信性能简直是跳跃式的发展,这主要归功于卷积码的发明。
卷积码是Elias在1955年提出的。
卷积码与分组码的不同在于:它充分利用了各个信息块之间的相关性。
通常卷积码记为(n,k,N)码。卷积码的编码过程是连续进行的,依次连续将每k个信息元输入编码器,得到n个码元,得到的码元中的检验元不仅与本码的信息元有关,还与以前时刻输入到编码器的信息元(反映在编码寄存器的内容上)有关。同样,在卷积码的译码过程中,不仅要从本码中提取译码信息,还要充分利用以前和以后时刻收到的码组。从这些码组中提取译码相关信息,而且译码也是可以连续进行的,这样可以保证卷积码的译码延时相对比较小。通常,在系统条件相同的条件下,在达到相同译码性能时,卷积码的信息块长度和码字长度都要比分组码的信息块长度和码字长度小,相应译码复杂性也小一些。
很明显,在不到10年的时间里,通信编码技术的发展是飞跃式的,直到遇到了瓶颈。
根据香农前辈的指示,要提高信号编码效率达到信道容量,就要使编码的分段尽可能加长而且使信息的编码尽可能随机。但是,这带来的困难是计算机科学里经常碰到的“计算复杂性”问题。
还好,这个世界有一个神奇的摩尔定律。
得益于摩尔定律,编码技术在一定程度上解决了计算复杂性和功耗问题。而随着摩尔定律而来的是,1967年,Viterbi提出了Viterbi译码算法。
在Viterbi译码算法提出之后,卷积码在通信系统中得到了极为广泛的应用,如GSM、 IS-95 CDMA、3G、商业卫星通信系统等。
但是,计算复杂性依然是一道迈不过的墙。
尽管人们后来在分组码、卷积码等基本编码方法的基础上提出了许多简化译码复杂性的方法,但是均因无比高耸的计算复杂性之墙阻挡而变得不可逾越。
编码专家们苦苦思索,试图在可接受的计算复杂性条件下设计编码和算法,以提高效率,但其增益与香农理论极限始终都存在2~3dB的差距。
直到1993年,在日内瓦召开的 IEEE通信国际会议上,两位当时名不见经传的法国电机工程师C.Berrou和A.Glavieux声称他们发明了一种编码方法,可以使信道编码效率接近香农极限。
这一消息太“轰动”了,因为几乎所有的专家都认为这俩“棒槌”是来捣乱的。
这么多数学家都没能突破,就你这两个小角色也敢宣称接近香农极限?不是存心捣乱吗?一定是计算上出了错误吧?
许多专家甚至懒得去读完这篇论文。
事实上,这两位法国老兄的数学功底可能真的不怎么样,他们没有试图从数学上找突破口,因此他们的论文在会上被怀疑和忽略就不足为奇了。
但是,专家们忽略了一个问题。凭着电机工程师的经验,他们发现在电子学中经常用到的反馈概念似乎被数学家们忽略。也许反馈能够使我们绕过计算复杂性问题,于是他们就设计了一套新的办法。
首先他们摈弃了“纯粹”的数字化概念。在典型的数字化方法中,总是先把某一电平设定为阈值。信号电平高于这一阈值就判决为“1”,低于就判决为“0”。在Turbo码解码过程中,某一特定比特的电平被量化为整数,例如从-127到+127。其数值就作为判决该比特为“1”或“0”的可置信度的度量(例如-110意味该比特非常非常可能是“0”,而+40 意味该比特也许是“1”但把握不大)。
其次,与其他系统不同,Turbo码系统在发射端和接收端分别设置两个编码器和解码器。其中一对编解码器对特定的一段比特流进行奇偶校验码的加入和校验计算,另一对编解码器则在同一段码流经过交织扰动后对其进行上述同样操作。
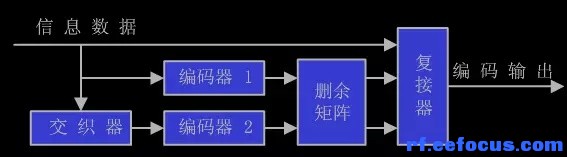
▲Turbo编码器结构。Turbo码编码器是由两个或多个反馈的系统卷积码编码器通过一个随机交织器并行连接而成,编码后的校验位经过删余矩阵,从而产生不同码率的码字。
由于这两段码流包含同样的数据,如果没有信道噪声,解码结果应该一致。但在噪声干扰下两组结果会产生差别。通过上述对比特判决的可置信度信息的帮助,把这两组结果彼此参照,可以得出第一次近似的结果。把这一结果“反馈”到解码器前端,再进行迭代,经过几次迭代两个解码器的结果就会互相接近(收敛)。这样就绕过了计算复杂性问题。
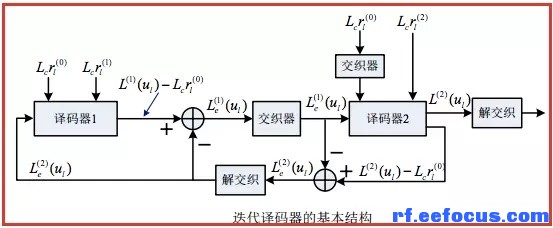
▲Turbo码的译码器有两个分量码译码器,译码在两个分量译码器之间进行迭代译码,故整个译码过程类似涡轮(turbo)工作,所以又形象的称为Turbo码。
当然这样做也得付出代价。由于迭代解码,必然会产生时延。所以对于实时性要求很高的场合,Turbo码直接应用会受到限制。
接下来,那些编码专家们跌破了眼镜。不可思议,当其他小组验证了这两位法国老兄的方案时,证明了结论是正确的。现在人们谈论的已经是和香农极限相差0.1dB还是0.01dB了。
一个通信编码史上的革命性的时代到来了!两位名不见经传的电机工程师不顾科学权威认定的种种“极限”,在一片嘲笑声中,另辟蹊径,突破了理论壁垒。
一开始,Turbo码只是应用于一些特殊场合,比如卫星链路。后来,研究人员将它扩展到数字音频和视频广播领域。
紧接着,Turbo码成为通信研究的前沿,全世界各大公司都聚焦在这个领域,包括法国电信、NTT、DoCoMo、索尼、NEC、朗讯、三星、爱立信、诺基亚 、 摩托罗拉和高通等等。
Turbo码成为了始于本世纪初的3G/4G移动通信技术的核心,直到今天4.5G,我们依然在采用。
现在,编码专家们都松了一口气,总算解决了这个棘手的问题。也同时都叹了一口气,因为这已经接近香农极限了,发现似乎在这领域已经很难再突破了。
收工,回家,带娃。
但是,在1999年,编码界又发生了一件有趣的事。人们重燃起了对LDPC的兴趣,尽管它已经被人们遗忘了几十年。
LDPC( low-density parity check),即低密度奇偶校验码。它于1962年由Gallager提出,然后,被人们遗忘了。直到Turbo码被提出以后,人们才发现Turbo码从某种角度上说也是一种LDPC码。
另一件让人们感兴趣的事是,LDPC码发明较早,其基本专利到1999年就到期了,而Turbo码要到2013年才到期。
LDPC利用校验矩阵的稀疏性,使得译码复杂度只与码长成线性关系,在长码长的情况下仍然可以有效的进行译码,因而具有更简单的译码算法。随着人们对 LDPC码重新进行了研究,发现LDPC 码与Turbo一样具有逼近香农极限的性能。较新的研究结果显示,实验中已找到的最好LDPC码,其极限性能距香农理论限仅相差0.0045dB。
接着,LDPC在IEEE 802.11n 以及802.16的技术提案中被热烈讨论。DVB-S2也决议以LDPC替代Turbo码。有人认为,LDPC是终极纠错编码,极有可能成为未来主流编码技术。
所以,一场关于Turbo码和LDPC码的争论就拉开了。随着5G标准化的到来,Turbo码和LDPC码像拳击台上两名重量级选手,两人都宣称自己将是获胜者,但裁判的结束哨声却一直未吹响。
裁判很头痛,这是一场几乎无法打分的比赛。因为,之所以有争论,无非是要证明,谁才更适合未来5G用例?谁才能更好满足新的技术需求?
众所周知,2G的应用场景是语音和低速率数据业务,3G和4G的应用场景是语音和更高速率的数据业务。可以确定的是,Turbo码和LDPC码都能很好的满足3/4G,甚至是4.5G用例。
而5G用例呢?市场上还没有出现,而且很多。不管是Turbo码,还是LDPC码,都无法确定谁才是最好的选择。而且,由于两者各有优缺点,要覆盖全部5G应用,不太现实。
正当Turbo码和LDPC码打拳击赛之时,Polar码冲上了拳台,变成了一场摔角运动。
很幸运,在编码技术不断打破记录带给我们惊喜时,另一项编码领域里的激动人心的研究已浮出水面。
2007年,土耳其比尔肯大学教授E. Arikan基于信道极化理论提出的一种线性信道编码方法,即Polar码。该码字是迄今发现的唯一一类能够达到香农限的编码方法,并且具有较低的编译码复杂度,当编码长度为N时,复杂度大小为O(NlogN)。
Polar码的理论基础就是信道极化。信道极化包括信道组合和信道分解部分。当组合信道的数目趋于无穷大时,则会出现极化现象:一部分信道将趋于无噪信道,另外一部分则趋于全噪信道,这种现象就是信道极化现象。无噪信道的传输速率将会达到信道容量I(W),而全噪信道的传输速率趋于零。Polar码的编码策略正是应用了这种现象的特性,利用无噪信道传输用户有用的信息,全噪信道传输约定的信息或者不传信息。
这就像一个班上的同学,上学时间足够长的话,差的学生大部分会跌到谷底,好的学生大部分会飞向云巅,然后,抛弃那些学渣…
Polar码比Turbo码和LDPC码更接近信道容量,Polar码可以保证5G任何场景的高性能通信。夸张的讲,如果不考虑系统设计问题,编码技术的历史就应该到此终结了,终结在Polar码的手里。
但是,编解码的复杂性是Polar的问题,不过,在使用改进后的SCL(Successive Cancelation List)译码算法时能以较低复杂度的代价,接近最大似然译码的性能。
关键是,Polar码还是太年轻了,发明得比较晚,很多研究还建立在理论基础上,不像Turbo码和LDPC码已经广泛应用于实际场景。只有等待时间来告诉我们,Polar码到底是不是5G信道编码的王者。
回顾信道编码历史,波澜壮阔。在几十年并不漫长的岁月里,一次又一次关键技术的历史性突破,造就了今天人类通信奇迹。而当5G即将到来之时,更令人兴奋的是,我们看到了各种优秀的编码技术的涌现。毫不夸张的说,这是信道编码技术的文艺复兴时期。而开启文艺复兴之门的,不仅仅是信道编码,5G将激发无线产业史无前例的创新活力。
