低通滤波器就是积分器你懂吗?个人心得,欢迎来讨论。
前几天在电子发烧友发了个帖子,问一个无源滤波器上的电压如何表示。因为从积分器与低通滤波器角度出发,从公式上出发相差很大的。好几天也没有回答的,今天下午突然看到了一个三角波的傅里叶分解,一下来了灵感,用了一个半小时左右终于想通了。图1是问题来源,图2是知识储备,,图3是自己画的结果。纯理论,没有滤波器的实验。欢迎大家指正错误。我不会插图,第一次发这种帖子。
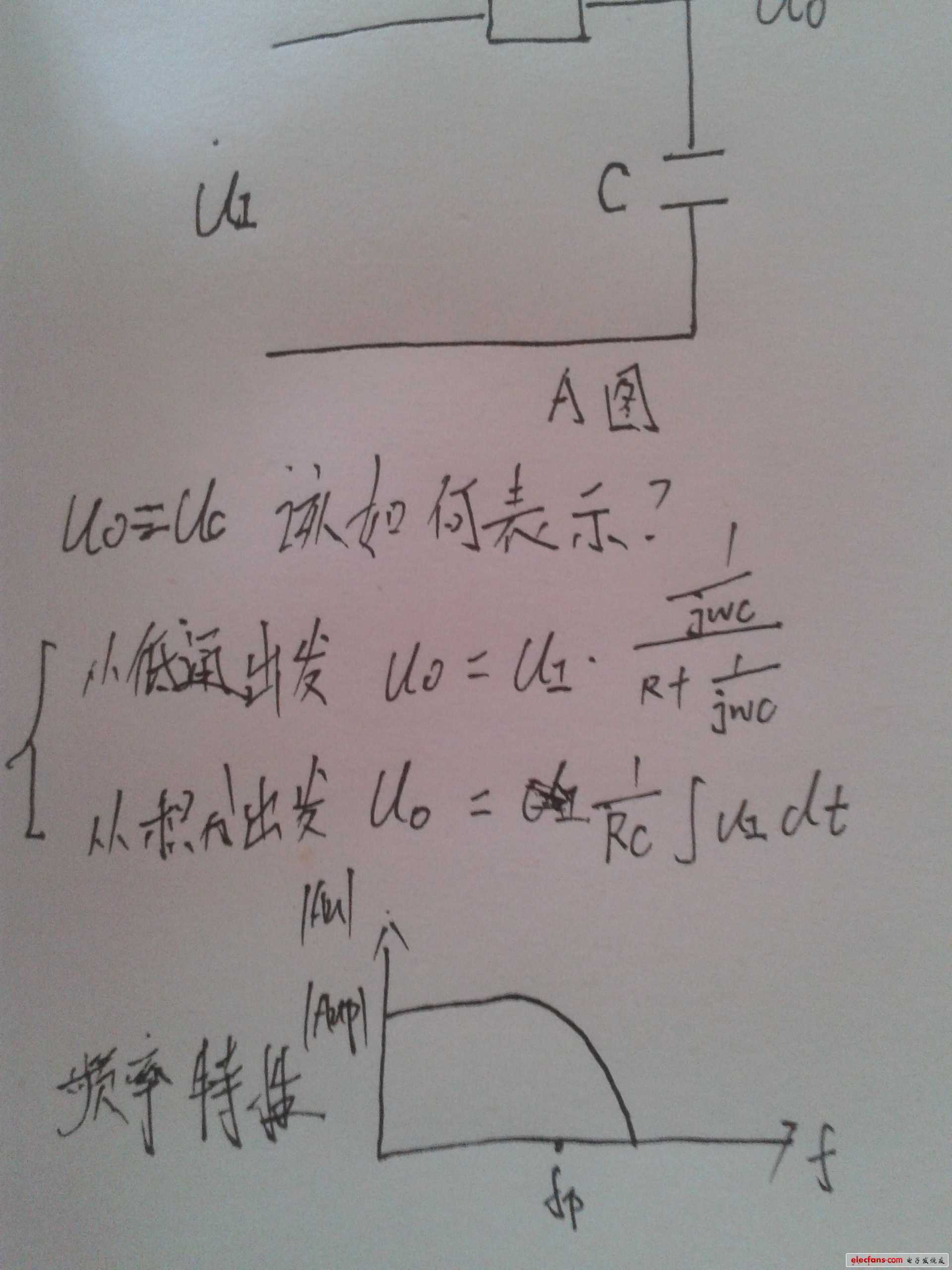

图三
以前我们学习基本的RC电路,说它是一个积分器,说它是一个低通滤波器。当然做题是没问题,但是没有从根本上理解。
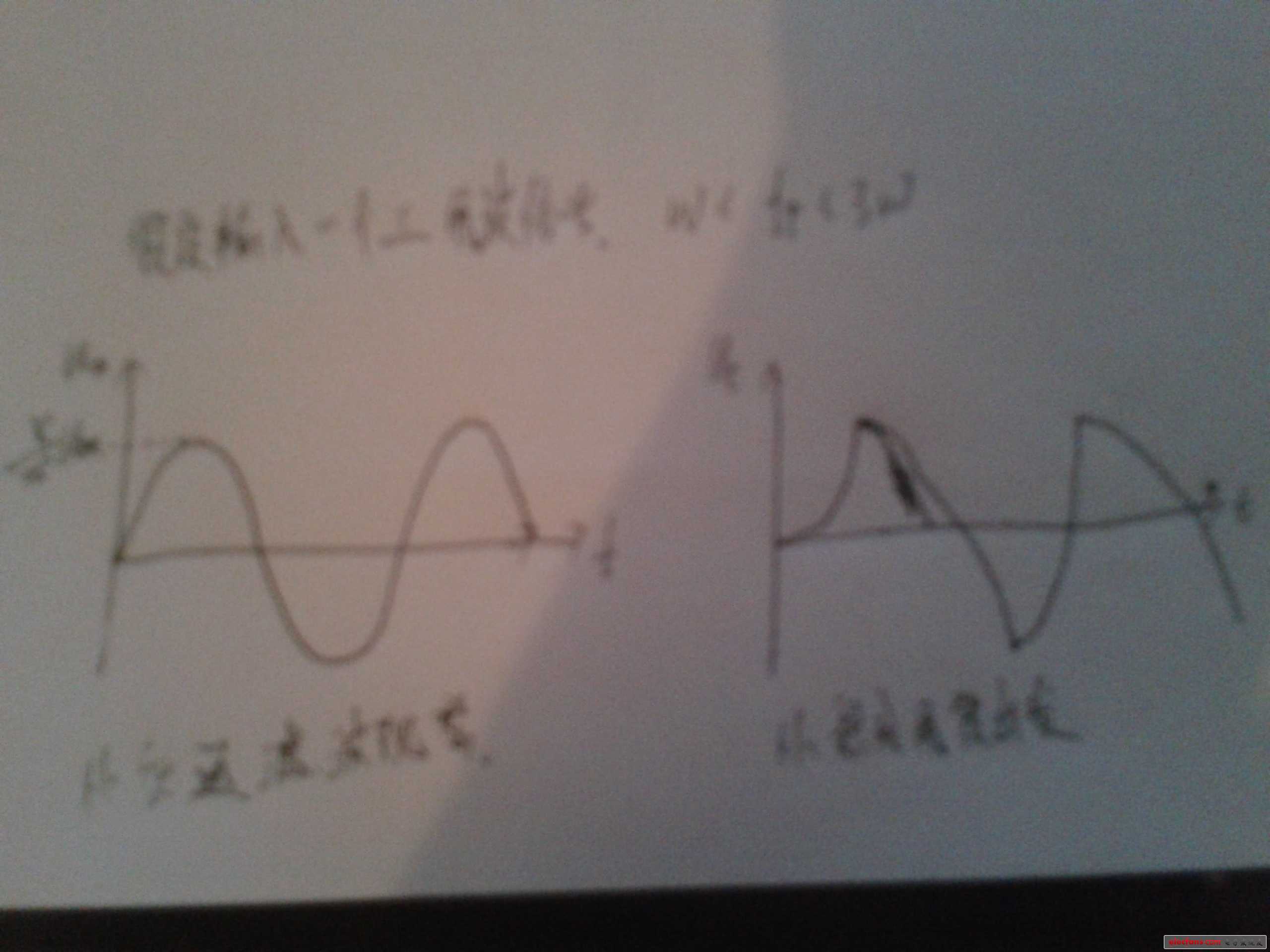
在我的图2中从知识储备开始,首先由一个方波输入,另一个波形输出,电容的充放电,凹凸性画的不太好。用这个例子主要是说明RC低通其实并不是一个精确的积分电路,确切的说是近似性积分电路。
第二个图呢?就是讲了一个三角波的傅里叶变化,这个没有什么好说的。学过高数也罢,学过信号与系统也罢,应该都可以推倒出来。图中三角波的幅度为Um。不清楚,我就打出来了。U(wt)=(8/π方)*Um*(sinwt—1/9sin3wt+1/25sin5wt……….)
我就以三角波为输入信号,观察其输出为例,做了一下分析。
从低通滤波来讲,假设上限截止频率w<fp<3w,那么经过低通滤波器后就剩下一个单频率的正弦信号,这个波形为Uo=8/Π2(Um*sin(wt)),就是8乘以Um*sinwt除以pi的平方。我不会打那些符号,抱歉。即输出波形在图中我们很清楚看到一个正弦波。
从积分器讲,三角波的话,设上升时候的斜率为K1,下降时候的频率为K2。即上升的时候y=k1*x,下降的时候y=k2*x+b。积分下可以得到UO1=k1/2*(x的平方),UO2=k2/2*(x的平方)+bx。K1>0,k2<0。根据输出的二次倒数可以判断出输出的凹凸性(突然想起大学时候示波器上显示的波形为啥有个“尖嘴”的原因)。输出为图中所示。
分析:为啥从两者看,图形有些不同呢?首先低通滤波器并不是说将高于3w的频率都滤去了,而是因为我们在分析的时候,认为高次谐波的幅值太小,将高次谐波忽略了。其次是从积分器出发,该电路并不是标准的积分电路,应该是约等于。也就是说这两个图其实都不太准确,不过也差不多,只是我画的可能有点夸张了吧。
结论:这是以低通滤波器为例子,代表的时候电容上电压的问题。最后我的结论就是,无论哪种表示方法,都正确就是系统不变,输入不变,输出也不变。观察角度不同而已。
附加感触:当然分析放大倍数的时候 我们用公式Au=1/(1+jrwc),其实我现在还不太懂,因为这个J(虚部),从图形上看两者的图形不是同类型的,不同类型波形的分析放大倍数,我觉得好怪啊。书上讲了|Au|。也
从时域到频域好理解,但是这个复数我现在好迷茫啊。就像电容的阻抗Z=1/jwc,j是什么,是相位的超前滞后,还是又多了一维………就像给我了一个五维,六维空间一样,暂时没有那个概念。尽管学过数学啊,数学物理方法(学的不好)。到底虚部j代表着什么。有谁理解的好可以说一下。
多亏占了沙发,今天我来终结此帖子。去年发帖后 我很快证明出来了,就是懒得上传,大家久等了。


那个。首先感谢分享。其次,小编,很棒。
这种原创东西甚是美妙
看看~~~~~~
这两个本来本质就是一样的,你一看表达形式,就能看出来的啊。低通滤波就是频域表达,而积分是时域表达;你学过自动控制的话,就应该不难理解了,等价的变换。但是再具体分析问题的时候,有时候使用时域更容易理解,那就用积分电路相关理论来解释。有时候用频率更容易理解,当然用低通滤波来解释。当遇到一般的噪声信号时候,就需要使用低通滤波来解释,因为噪声信号一般都是高频,所以使用他就很容易理解。而当对于确实需要一个信号变换时候(单纯的信号积分),使用积分电路可以的到你想要的输入波形或者信号。这样使用积分电路理论就很显然了
………………………………………………
好,有勇气
顶小编,好童鞋!
学习了,一直认为j是系统中频率对相位的影响!
赞同
好,有勇气
我是学电气的,现在才大二,小编说的这些都还懂哩
我还没工作,仅仅是在上学而已,水平比较次,勿喷。可能有错误的地方。111
我也知道是频域时域表示,只是做题的时候,遇到这个东西了,到底表达式该怎么表示呢?就是用一个例子验证下自己的结论。
很简单的东西,其实。你学了信号与系统就更懂了。我只想验证下这个结论。
