一个简单的负反馈型运放接法加个电容会怎样?

vin是一个正弦电压源,问会不会出现vin频率上升到某个频率,电路不稳定了?
我怎么看这个电路永远不会不稳定啊?
有输入,没看到输出啊,对于高频,电容相当于短路了
按原件参数列拉普拉斯方程判断极点零点估计能看出来 路过~~
肯定会不稳定
频率超过由R1、C决定的零点后,增益逐渐变大,但不会无限的增大下去,而是受限于OP的开环增益。
仿真的数据能看到OP的输出在高于零点频率后会有一个相位突变,这里的增益也最大,还没想明白为什么会有相位突变。
是否为电容移相造成的
学习中。。
对,是由电容的移相造成的,仿真的模型应该是给反馈电阻R2加了一个小的寄生电容。
信号频率高于零点的频率以后,以20dB的斜率上升,相位升高90度,频率再升高,会进入由两个电容决定增益的阶段,增值会有一个尖峰,这时反馈回路几乎是容性,然后相位突变。频率再升高,就会受到OP的开环增益限制,然后增益开始下降。
分析的非常专业
这个题如果只给出了电路,没有明确电路参数,那要考的东西就多了。
如果C1足够小,小到nF、pF的级别就不会振荡,也就是说由R1、C1构成的零点的频率很高,以至于闭环带宽内(增益带宽积)没有对增益产生影响,那就不会振荡。
而如果C1足够大,大到uF级别,R1、C1构成的零点的频率很低,明显低于电路的闭环带宽,也就是说从较低的频率开始增益就开逐渐变大,那肯定就要振荡了。
所以这个电路不同的参数有不同的答案,如果觉得难理解可以自己仿真下电路看看。
多谢BigMountain 提醒,下述文字有重大错误(起点错误)!。我抽空更新~! 留着目的是让大家都看看错在那里了!
我不太同意您的观点。我认为理想运放系统是稳定的。实际运放,可能不稳定!
首先,从理论计算上,这个电路的传递函数为 A(ω)=(1+Rf/R1)+jω(Rf)C 暂且定义A0=1+Rf/R1 ,s=jω
则传递函数A=A0+s*(Rf)*C
|A|=√(A0^2+((Rf)*C)^2) >0
ψ =arctan((Rf)*C/A0) 我们都知道反正切值域在 (-90°,90°)
所以,自激震荡的条件是,|A|>0时存ψ变换(2n+1)*Pi;在对于理想运放,开环增益无穷大的情况,上面的无法满足自激的相位条件。所以,说系统是稳定的。
而对于实际运放,要看其本身特性是否有足够的相位裕度(>=180度。),若相位裕度>=180度不会自激,
实际运放不可能做到相位裕度>180度,所以,实际运放,是会存在这个自激点的!
此外,从仿真的角度来看,同样可以说明反馈电阻和C的选择对与幅度,相位特性的影响!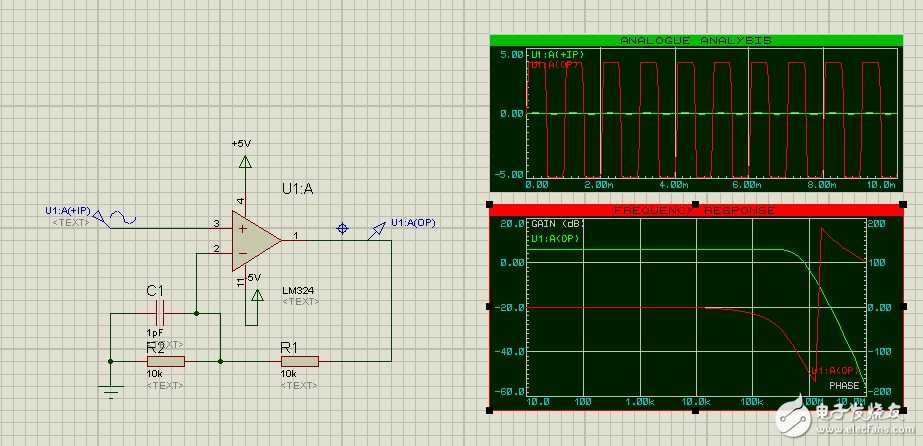
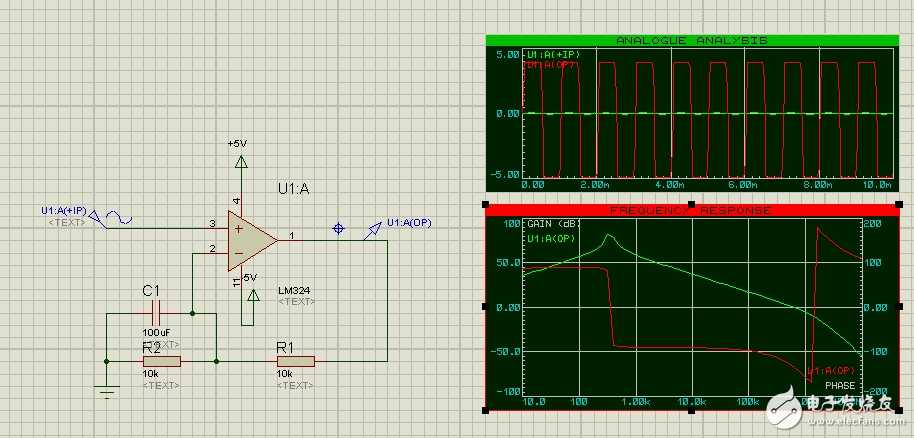
小编,TI的面试官给出的结果如何啊!
我分析时,输入频率上升,理想运放,系统会稳定!而实际运放,由于其相位裕度无法满足>=180所以,存在不稳定频率点的可能!
详细分析见11楼
其实还有一个简单的分析方法,显然电路只有一个C,一阶电路是稳定的,所以理想运放系统稳定!但是运放本身是多阶系统,所以就存在了不稳定可能!
淡定,兄弟,技术交流啊!
关于“闭环系统的稳定” 我的理解定义就是不自激!
理由是,对于多数系统,例如最常见的音频系统,都会存在-3db带宽问题。也就是说,输入不同频率一定会存在放大倍数“”不稳定“”变化的情况。如下图。如果是按照您的说法,没有在实际状态下,没有一个系统是稳定的了
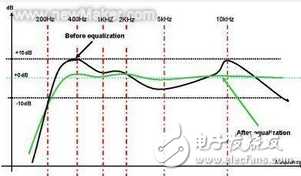
另外,自动控制系统中的阶跃响应的理想状态也都是增益收敛性震荡!
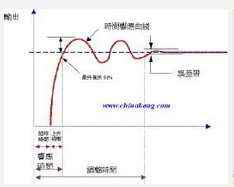
“”第二个仿真在几百赫兹的时候都已经冲到80、90dB左右了,难道这样的情况还能称之为稳定?这时一个很小的mV级别的输入就会电路输出饱和、振荡,造成不稳定!“”
虽然第二个图 有90db上升,但是此时的 相位不满足(2n+1)*Pi的条件,所以电路不会震荡。对否?
另外,下述摘自百度文库
对于系统稳定性的判定,控制学家们提出了很多系统稳定与否的判定定理。这些定理都是基于系统的数学模型,根据数学模型的形式,经过一定的计算就能够得出稳定与否的结论,其中,主要的判定方法有:劳斯判据、赫尔维茨判据、李亚谱若夫三个定理。这些稳定性的判别方法分别适合于不同的数学模型,前两者主要是通过判断系统的特征值是否小于零来判定系统是否稳定,后者主要是通过考察系统能量是否衰减来判定稳定性。
具体到使用方法及形式上,可分为下列三种具体的判定方法:
从闭环系统的零、极点来看,只要闭环系统的特征方程的根都分布在s平面的左半平面,系统就是稳定的。
1、劳斯判据:
判定多项式方程在S平面的右半平面是否存在根的充要判据。——特征方程具有正实部根的数目与劳斯表第一列中符号变化的次数相同。
2、奈奎斯特判据:
利用开环频率的几何特性来判断闭环系统的稳定性和稳定性程度,更便于分析开环参数和结构变化对闭环系统瞬态性能影响。——利用幅角原理——Z、P分别为右半平面闭环、开环极点,要想闭环系统稳定,则Z=P+N=0,其中N为开环频率特性曲线GH(jw)顺时针绕(-1,j0)的圈数。
3、波特图:
幅值裕度——系统开环频率特性相位为-180时(穿越频率),其幅值倒数K,意义为闭环稳定系统,如果系统的开环传递系数再增大K倍,系统临界稳定。
相位裕度——系统开环频率特性的幅值为1时(截止频率),其相位与180之和。意义为:闭环稳定系统,如果系统开环频率特性再滞后r,系统进入临界稳定。
一直很淡定啊,哈哈
可能考虑的角度不一样,你一提到振荡可能考虑的就是自激振荡,那对于我来说还有可能是其它情况引起的输出振荡,也就是我一直说的那种情况,闭环带宽内增益出现很大的尖峰,你说的音频系统可不是这种响应曲线,
好了就这样吧,知道想要表达的意思就可以了,本来就种题出出来就有很多问题。
PS: 你的最后一张图应该是阶跃响应的输出响应图吧,是因为系统的阻尼系统太小,导致短暂的过冲及振荡,对应到bode图上,3dB附近会有相应的一个尖峰。
坐等小编公布面试官回复啊!
首先感谢这么多大神的回复,看完很受启发。
当然,答案我也不知道。做完题目去面试五分钟就刷掉了,哪还有脸面留下来问问题。
