RC延时电路分析
RC延时电路分析
电阻R、电容C、电动势E与开关K彼此相互串联,构成有源闭合回路,如图1所示。
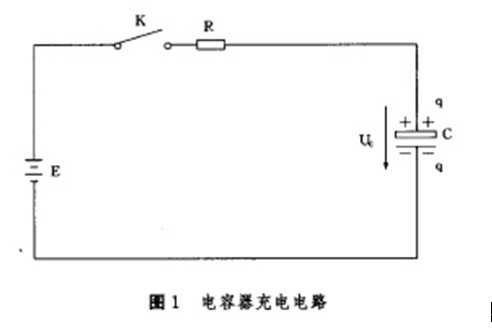
当开关K合上后的一段时间内,电路中有电流I通过,电动势E通过电阻R向电容C充电,电容器上的电压Uc逐渐升高,因R、C、E是常量,而Uc、I是变量,故根据回路电压定律,可得:
E= IR+Uc (1)
因为△t时间内,电路中任意横截面上的平均电流等于电量的变化量,即I=dQ/dt,也就是说电流I是电容C上的电荷Q对时间t的导数。另根据电容器的定义,Q=CUc,因此
I=dQ/dt=d(CUc)/dt=CdUc/dt(2)
用(2)式代入(1)式得:
E=RCdUc/dt+Uc(3)
将方程(3)进行分离变量得:dUc/(E-Uc)=dt/RC,两边积分,

对于(3)式一个含有未知函数Uc(t)的微分方程,其初始条件,开关K刚合上的瞬间时t=0,这时电容器上的电压变化量Uc为零,
即(Uc/t=0)=0,(4)
其中a是任意常数,把初始条件(4)式代入(5)式得a=-LnE,把a的值代入(5)式得-Ln(E-Uc)=1/RC.t-LnE,整理可得LnE-Ln(E-Uc)=(1/RC)*t (6),即
t=RC*Ln[E/(E-Uc)], (7)
对(7)式去对数,变为E/(E-Uc)=et/rc,最后得到Uc=E[1- 1/et/rc)。可见,电容器两端电压的变化与时间的指示函数e-t/RC有关,如图2所示,充电开始时,t=0,Uc=0,I=E/R(最大值),最后I=0,Uc=E(最大值)。
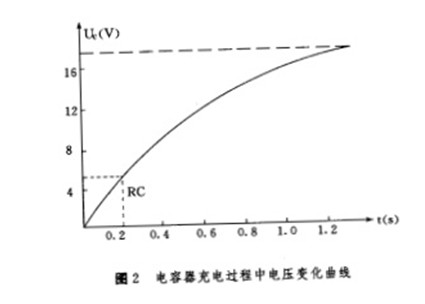
2 延时电路RC参数的选择
从以上分析可知,电容器充电速度与R和C的大小有关,即C越大,充至同样电压所需的电荷越多,Uc上升的也就越慢,R越大,充电电流就越小,Uc上升也就越慢。
好好!
可以理解!
明了
简单易懂
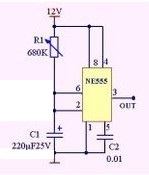
问个问题,我这样的电路怎么有时候2-6脚电压会忽高忽低,我检查我焊接的电路 没发现有短路的,电压一直上不去,各位大哥帮忙分析一下
受教育了!!

大概是电阻电容不匹配 引起振荡了 换换电容试试看
不错不错不错不错
小知识蕴含着大道理。顶一个。
鼓掌!太好了
学习了
很好!学习了!
不错,长见识了,以前到没有怎么注意到这些。
看来要学习下微分和积分电路了
very goodvery goodvery goodvery good
