基于OFDM系统的频域同步估计技术
时间:08-14
来源:互联网
点击:
同步部分概述
正交频分复用(OFDM)系统的一个重要问题是对频率偏移非常敏感,很小的频率偏移都会造成系统性能的严重下降。另外收发端采样钟不匹配,也会导致有用数据信号相位旋转和幅度衰减,破坏了OFDM子载波间的正交性,降低系统性能。因此在OFDM系统中,频率偏移和采样钟偏移估计的准确度至关重要。
OFDM接收系统的同步部分主要包括以下几方面:频率同步、采样钟同步和符号定时同步。载波频率偏移和采样钟频率偏移的存在导致了载波间干扰(ICI)和采样点增减现象,这就需要频率同步和采样钟同步。同时在解调过程中,接收机是在时域上的任意点开始接收数据的,而OFDM是基于符号的,这就需要检测到符号的起始位置,否则会因为符号的起始位置的不合理,而导致符号间的干扰(ISI),这就是符号定时同步。
频域同步估计方法
整数倍频率偏移估计算法
频率偏移△f0分成两部分:整数倍和小数倍子载波间隔频偏。由于在时域上已经对小数倍频偏有一个粗略估计和校正,因此频域内是利用内插导频信息对整数倍频偏和剩余小数倍频偏进行估计校正的。
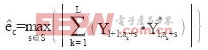 (1)
(1)
式(1)是整数倍频率偏移估计算法表达式,它是利用连续导频在发射端为已知固定相位的特性,使用一个长为S的滑动窗作为频域上一个OFDM符号有效载波起始位置的估计范围,以窗内的每一个数据作为OFDM符号有效载波的的起始位置,对前后两个符号在假设的连续导频位置上的复数据做相关求和,这样就得到了S个相关值,其中最大值所对应的s即为频域上一个OFDM符号有效载波起始位置的估计值,也即为整数倍频偏估计值。
其中L是连续导频个数;ak是一个符号内第k个连续导频的序号;Yl,ak是FFT输出的第l个符号的假设第k个连续导频位置上的复数值;S是整数倍频偏的估计范围,也即为滑动窗长,s是窗口移动值,s∈S;
是S路相关和的最大值,其对应的s即为整数倍频偏的估计值。
小数倍频率偏移和采样钟频率偏移估计算法
在OFDM系统的接收端,实际的第m个子载波的实际解调频率为f'm=f'0+mF',这里,f'0为本地解调载波频率,F)=F'0N,N为子载波个数,F'0为接收机压控晶振输出的采样频率。由此可以看出,在第m个子载波上,载波频偏和采样钟偏移的联合效应是大小等于△fm的子载波频偏,这里△fm=△f0+m?△F0N,△f0=f'0-f0,△F0=F'0-F0,f0和F0分别为发射端的中心载波频率和采用频率。当将整偏校掉后,这里的△f0仅为小数倍的子载波间隔。
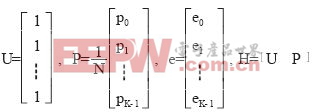
设pi为导频点位置,pi∈P,P为导频点位置集合;i=0,1,…,K-1,K是P的基数;△fpi为第pi个导频点上相关结果的频率部分,这个值以下用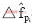 表示为估计结果。定义
表示为估计结果。定义

,同时考虑到在第pi个子载波上的估计误差ei,则:
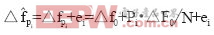 (2)
(2)
其中,△fpi为在第pi个导频点上的频率偏移和采样钟偏移之和,现令
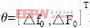
为所需估计的向量参数,式(2)就可以写作:
 (3)
(3)
其中,
由于估计是基于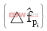 的,因此将向量V称为观察向量,方程式(3)称为观察方程。线性最小平方估计就是在观察向量给定的条件下,根据观察方程估计向量
的,因此将向量V称为观察向量,方程式(3)称为观察方程。线性最小平方估计就是在观察向量给定的条件下,根据观察方程估计向量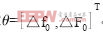 。根据最大似然估计原理,使得向量V的线性函数
。根据最大似然估计原理,使得向量V的线性函数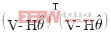 取得最小值时,得出
取得最小值时,得出 的估计值
的估计值 。对式
。对式
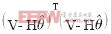 求导并使之为零,可得:
求导并使之为零,可得: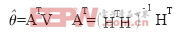 (4)
(4)
公式(3)是在先得出
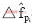
,i=0,...,K-1的基础上求得的,而
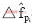
可以通过在导频位置对前后两个OFDM符号做相关运算来求。
频域符号定时偏移估计算法
时域定时的不准确就要求频域内进一步对OFDM符号定时进行校正。由于时域内保护间隔是数据信号最后L个采样点的完全复制,所以由FFT循环移位定理可知:符号定时的偏移所引起的子载波上相位旋转和子载波序号k成正比。由于导频信号插入位置已知,且其具有相位已知特性,这使得我们可以利用符号内插导频载波间相位变化来做细符号定时同步,并与粗符号定时同步结合起来,得到一个准确的符号起始位置。
设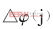 是第j个OFDM符号定时偏移在相邻导频点上所引起的相位偏移之差,
是第j个OFDM符号定时偏移在相邻导频点上所引起的相位偏移之差,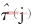 为第j个OFDM符号所估计出来的细定时。则
为第j个OFDM符号所估计出来的细定时。则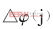 和
和
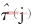 可表示为:
可表示为:
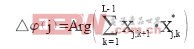 (5)
(5)
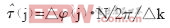 (6)
(6)
其中,L为散布导频个数;N为一个OFDM符号中有效子载波的个数;Xj,k是第j个符号的第k个散布导频复值;△k为两个相邻的子载波序号的差值。
频域同步部分的FPGA电路实现模块
频域同步电路模块各单元的工作原理如图3.1所示。这里使用Altera公司生产的StratixⅡEP2S60的FPGA芯片来实现。
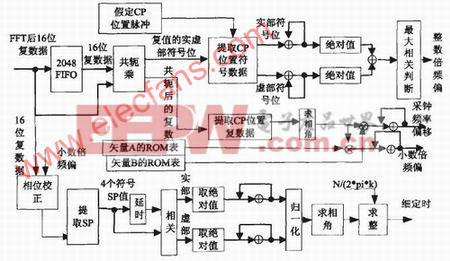
图3.1 FFT后同步块方框图
FFT模块输出复数据经过一个OFDM符号的FIFO模块延迟后,和当前的OFDM复数据进行相关,以实现在整数倍频偏估计和小数倍频率偏移算法中所需要的前后两个符号的对应导频相关运算,其相关结果为32位的复数据。
整数倍频率偏移估计模块
将相关单元输出的复数据的实虚部符号位送到整数倍频偏估计单元中进行整数倍频偏估计。为了节省芯片资源,这里我们将估计整数倍频偏的算法加以简化,用相关后的复数据在导频位置上的实虚部的符号位来估计整数倍频偏值。下面的仿真的电路波形图证明这样实现整偏估计算法是可行的。它的输入为相关单元输出的复数据实虚部的符号位和此复数据的载波同步位置,输出为整数倍频偏估计值。
小数倍频率偏移和采样钟频率偏移模块
首先对相关单元模块输出的复数据的实虚部进行归一化,然后求归一化单元输出的16位复数据的相角,同时用RAM的读地址和读使能信号分别控制读取存有矢量A和矢量B数据的ROM表中的数据。其中矢量A和B分别为线性最小平方估计算法中矩阵AT的第一行和第二行矢量,用此相角分别和读出的矢量A和矢量B在一个符号内进行相乘累加,再根据保护间隔的不同,乘以相应的系数,便可分别得到小数倍频偏和采样钟频率偏移的估计值。
细定时估计模块
考虑到定时估计范围的问题,该模块利用四个符号的散布导频进行定时估计。将当前符号的散布导频值及从RAM中读出的前三个符号的散布导频值按一定顺序排列,并做相邻导频相关。将相关后的复数据的实虚部分别取绝对值累加,并将二者的累加和进行归一化处理后进行查表,从而得出复数的相位值。这个相位即为符号定时偏移所引起的旋转相位。再对此相位做如公式(6)的运算,这样就得到了符号定时偏移的整数和小数部分的和,然后将其送到求整函数中,从而得到符号定时偏移的整数部分。将这个值经过并/串变换后送到前端时域同步部分,去调整FFT窗位。
电路仿真
其仿真条件为:瑞利信道,SNR为15dB,载波频偏设为-14.9倍子载波间隔(即整数倍频偏值为-15,小数倍频偏值为0.1倍子载波间隔),采样钟偏移为50ppm,保护间隔长为512,定时符号偏移为-100个采样点。此电路工作频率为10MHz。输入的16位复数据由MATLAB仿真程序产生的。
整数倍频率偏移电路仿真
由于电路波形中无法表示小数,因此将各小数进行“扩展”,其表示皆为二进制数据,以下同。在图4.1中,out_re[31]和out_im[31]分别是前后两个OFDM符号中对应子载波相关结果的实虚部的符号位,int_freqoffset[5..0]和syn_int分别是整数倍频偏估值和其有效起始位置脉冲。

图4.1 整数倍频偏估计部分的电路仿真波形图
由于整数倍频偏在每一符号的结束处才能估计出来,所以syn_int在每一个符号的结束处出现,其后即为当前符号的整数倍频偏值。由于本算法利用了4个符号的连续导频,故图4.1中,从第四个syn_int后的int_freqoffset[5..0]才是当前符号的整数倍频偏估计值。由仿真波形可看出,估出的整数倍频偏与仿真数据中所假设的一致。故用此算法的简化形式可以准确地估计出整数倍频偏值。
小数倍频率偏移及采样钟频率偏移估计的电路仿真
sernum[1..0]表示前级输入的符号类型;syn为输入复数据中的有用数据起始脉冲;rein[15..0]和imin[15..0]分别为FIFO模块输出复数据的实虚部;syn_offset为小数倍频偏和采样钟偏移估计结果的起始位置;fri[14..0]和qdelt[14..0]为小数倍频偏估计值和采样钟偏移估计值,它们由1位符号位和14位小数位组成。这里的小数位数是根据其估计范围和估计精度要求来确定的。
在图4.2中,小数倍频率偏移和采样钟频率偏移估计模块使用连续导频进行估计。在每个符号末,syn_offset高电平有效时,fri[14..0]和qdelt[14..0]才是当前符号的小数倍频率偏移和采样钟频率偏移估计值。波形中的估值与实际数据的对应关系如表4.1所示。

图4.2 小数倍频偏和采样钟偏移估计单元的电路仿真波形图
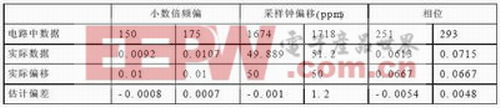
表4.1 波形图中数据与实际数据对照表
小数倍频率偏移和采样钟频率偏移模块是在整偏校完之后才有效,此时的小数倍频率偏移是经过时域粗偏估计校正后的剩余部分。表4.1列出波形中的估值与实际数据的对应关系。从表中的数字对应关系可以看出,电路中估计的小数倍频偏与实际频偏的差在0.1%以内。采样钟偏移估计值与实际偏移误差为1ppm左右,这已满足了采样钟的粗调精度;相位输出为前后符号的小数倍偏频所引起的相位旋转。由此单元电路,可以准确地估计出小数倍频偏和采样钟偏移及其相位。
细定时同步估计的电路仿真
图中的data_re_in[15..0]和data_im_in[15..0]表示经公共相位校正后的复数据实虚部;syn_in是输入有用数据的起始位置脉冲;sym_type[1..0]是前端输入的符号类型;taok[22..0]和td[9..0]分别为估计的符号定时偏移和其整数部分;syn_tao是taok[22..0]的有效数据起始脉冲信号。

图4.3 符号定时偏移估计单元的电路波形图
图4.3中共有9个符号。由于本算法利用了4个符号的散布导频,故图4.3中,从第四个符号的结束处开始,在syn_tao后的taok[22..0]才是当前符号的定时偏移估计值。波形中的估值与实际数据的对应关系如表4.2所示。
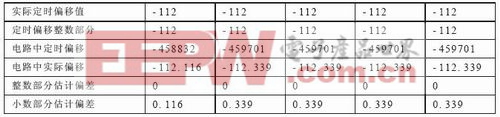
表4.2 波形图中数据与实际数据对照表
表4.2中的定时实际偏移为-112,而不是仿真条件中的-100,这是由于在瑞利信道的仿真模型中,符号定时同步头位置(重心位置)是在第一条径之后12个采样点出现的。由表中数据对应关系可知,符号定时偏移估计单元可准确地估出符号定时偏移的整数部分。由于采样钟偏移、算法估计误差及电路运算误差的影响,其小数部分不为零,这与电路的仿真结果一致。
改进前后占用硬件资源比较
表4.3给出了改进前后,频域同步所占用的硬件资源比较,其中ALUTS、Registers、Memorybits、DSPblock9-bitelements分别为自适应查找表、寄存器、存储器和9字节DSP处理块。通过比较可以发现,改进后的方案可以节省大量的硬件资源。

表4.3 改进前后的硬件资源对比
结束语
频率偏移估计可以分为整数倍频偏估计单元、小数倍频偏、采样钟偏移估计单元和符号定时偏移估计单元。本文主要介绍各部分的算法方案及电路实现时所用的FPGA元件的基本结构、设计思路。最后通过对电路的仿真波形可以看出,这些频域同步算法和FPGA电路能够满足多载波传输系统的同步要求。
正交频分复用(OFDM)系统的一个重要问题是对频率偏移非常敏感,很小的频率偏移都会造成系统性能的严重下降。另外收发端采样钟不匹配,也会导致有用数据信号相位旋转和幅度衰减,破坏了OFDM子载波间的正交性,降低系统性能。因此在OFDM系统中,频率偏移和采样钟偏移估计的准确度至关重要。
OFDM接收系统的同步部分主要包括以下几方面:频率同步、采样钟同步和符号定时同步。载波频率偏移和采样钟频率偏移的存在导致了载波间干扰(ICI)和采样点增减现象,这就需要频率同步和采样钟同步。同时在解调过程中,接收机是在时域上的任意点开始接收数据的,而OFDM是基于符号的,这就需要检测到符号的起始位置,否则会因为符号的起始位置的不合理,而导致符号间的干扰(ISI),这就是符号定时同步。
频域同步估计方法
整数倍频率偏移估计算法
频率偏移△f0分成两部分:整数倍和小数倍子载波间隔频偏。由于在时域上已经对小数倍频偏有一个粗略估计和校正,因此频域内是利用内插导频信息对整数倍频偏和剩余小数倍频偏进行估计校正的。
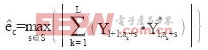 (1)
(1)式(1)是整数倍频率偏移估计算法表达式,它是利用连续导频在发射端为已知固定相位的特性,使用一个长为S的滑动窗作为频域上一个OFDM符号有效载波起始位置的估计范围,以窗内的每一个数据作为OFDM符号有效载波的的起始位置,对前后两个符号在假设的连续导频位置上的复数据做相关求和,这样就得到了S个相关值,其中最大值所对应的s即为频域上一个OFDM符号有效载波起始位置的估计值,也即为整数倍频偏估计值。
其中L是连续导频个数;ak是一个符号内第k个连续导频的序号;Yl,ak是FFT输出的第l个符号的假设第k个连续导频位置上的复数值;S是整数倍频偏的估计范围,也即为滑动窗长,s是窗口移动值,s∈S;
是S路相关和的最大值,其对应的s即为整数倍频偏的估计值。
小数倍频率偏移和采样钟频率偏移估计算法
在OFDM系统的接收端,实际的第m个子载波的实际解调频率为f'm=f'0+mF',这里,f'0为本地解调载波频率,F)=F'0N,N为子载波个数,F'0为接收机压控晶振输出的采样频率。由此可以看出,在第m个子载波上,载波频偏和采样钟偏移的联合效应是大小等于△fm的子载波频偏,这里△fm=△f0+m?△F0N,△f0=f'0-f0,△F0=F'0-F0,f0和F0分别为发射端的中心载波频率和采用频率。当将整偏校掉后,这里的△f0仅为小数倍的子载波间隔。
设pi为导频点位置,pi∈P,P为导频点位置集合;i=0,1,…,K-1,K是P的基数;△fpi为第pi个导频点上相关结果的频率部分,这个值以下用

,同时考虑到在第pi个子载波上的估计误差ei,则:
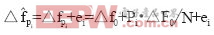 (2)
(2)其中,△fpi为在第pi个导频点上的频率偏移和采样钟偏移之和,现令
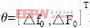
为所需估计的向量参数,式(2)就可以写作:
 (3)
(3)其中,

由于估计是基于
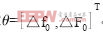 。根据最大似然估计原理,使得向量V的线性函数
。根据最大似然估计原理,使得向量V的线性函数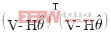 取得最小值时,得出
取得最小值时,得出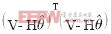 求导并使之为零,可得:
求导并使之为零,可得: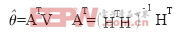 (4)
(4)公式(3)是在先得出
,i=0,...,K-1的基础上求得的,而
可以通过在导频位置对前后两个OFDM符号做相关运算来求。
频域符号定时偏移估计算法
时域定时的不准确就要求频域内进一步对OFDM符号定时进行校正。由于时域内保护间隔是数据信号最后L个采样点的完全复制,所以由FFT循环移位定理可知:符号定时的偏移所引起的子载波上相位旋转和子载波序号k成正比。由于导频信号插入位置已知,且其具有相位已知特性,这使得我们可以利用符号内插导频载波间相位变化来做细符号定时同步,并与粗符号定时同步结合起来,得到一个准确的符号起始位置。
设
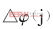 是第j个OFDM符号定时偏移在相邻导频点上所引起的相位偏移之差,
是第j个OFDM符号定时偏移在相邻导频点上所引起的相位偏移之差,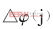 和
和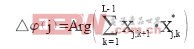 (5)
(5)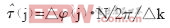 (6)
(6)其中,L为散布导频个数;N为一个OFDM符号中有效子载波的个数;Xj,k是第j个符号的第k个散布导频复值;△k为两个相邻的子载波序号的差值。
频域同步部分的FPGA电路实现模块
频域同步电路模块各单元的工作原理如图3.1所示。这里使用Altera公司生产的StratixⅡEP2S60的FPGA芯片来实现。

图3.1 FFT后同步块方框图
FFT模块输出复数据经过一个OFDM符号的FIFO模块延迟后,和当前的OFDM复数据进行相关,以实现在整数倍频偏估计和小数倍频率偏移算法中所需要的前后两个符号的对应导频相关运算,其相关结果为32位的复数据。
整数倍频率偏移估计模块
将相关单元输出的复数据的实虚部符号位送到整数倍频偏估计单元中进行整数倍频偏估计。为了节省芯片资源,这里我们将估计整数倍频偏的算法加以简化,用相关后的复数据在导频位置上的实虚部的符号位来估计整数倍频偏值。下面的仿真的电路波形图证明这样实现整偏估计算法是可行的。它的输入为相关单元输出的复数据实虚部的符号位和此复数据的载波同步位置,输出为整数倍频偏估计值。
小数倍频率偏移和采样钟频率偏移模块
首先对相关单元模块输出的复数据的实虚部进行归一化,然后求归一化单元输出的16位复数据的相角,同时用RAM的读地址和读使能信号分别控制读取存有矢量A和矢量B数据的ROM表中的数据。其中矢量A和B分别为线性最小平方估计算法中矩阵AT的第一行和第二行矢量,用此相角分别和读出的矢量A和矢量B在一个符号内进行相乘累加,再根据保护间隔的不同,乘以相应的系数,便可分别得到小数倍频偏和采样钟频率偏移的估计值。
细定时估计模块
考虑到定时估计范围的问题,该模块利用四个符号的散布导频进行定时估计。将当前符号的散布导频值及从RAM中读出的前三个符号的散布导频值按一定顺序排列,并做相邻导频相关。将相关后的复数据的实虚部分别取绝对值累加,并将二者的累加和进行归一化处理后进行查表,从而得出复数的相位值。这个相位即为符号定时偏移所引起的旋转相位。再对此相位做如公式(6)的运算,这样就得到了符号定时偏移的整数和小数部分的和,然后将其送到求整函数中,从而得到符号定时偏移的整数部分。将这个值经过并/串变换后送到前端时域同步部分,去调整FFT窗位。
电路仿真
其仿真条件为:瑞利信道,SNR为15dB,载波频偏设为-14.9倍子载波间隔(即整数倍频偏值为-15,小数倍频偏值为0.1倍子载波间隔),采样钟偏移为50ppm,保护间隔长为512,定时符号偏移为-100个采样点。此电路工作频率为10MHz。输入的16位复数据由MATLAB仿真程序产生的。
整数倍频率偏移电路仿真
由于电路波形中无法表示小数,因此将各小数进行“扩展”,其表示皆为二进制数据,以下同。在图4.1中,out_re[31]和out_im[31]分别是前后两个OFDM符号中对应子载波相关结果的实虚部的符号位,int_freqoffset[5..0]和syn_int分别是整数倍频偏估值和其有效起始位置脉冲。

图4.1 整数倍频偏估计部分的电路仿真波形图
由于整数倍频偏在每一符号的结束处才能估计出来,所以syn_int在每一个符号的结束处出现,其后即为当前符号的整数倍频偏值。由于本算法利用了4个符号的连续导频,故图4.1中,从第四个syn_int后的int_freqoffset[5..0]才是当前符号的整数倍频偏估计值。由仿真波形可看出,估出的整数倍频偏与仿真数据中所假设的一致。故用此算法的简化形式可以准确地估计出整数倍频偏值。
小数倍频率偏移及采样钟频率偏移估计的电路仿真
sernum[1..0]表示前级输入的符号类型;syn为输入复数据中的有用数据起始脉冲;rein[15..0]和imin[15..0]分别为FIFO模块输出复数据的实虚部;syn_offset为小数倍频偏和采样钟偏移估计结果的起始位置;fri[14..0]和qdelt[14..0]为小数倍频偏估计值和采样钟偏移估计值,它们由1位符号位和14位小数位组成。这里的小数位数是根据其估计范围和估计精度要求来确定的。
在图4.2中,小数倍频率偏移和采样钟频率偏移估计模块使用连续导频进行估计。在每个符号末,syn_offset高电平有效时,fri[14..0]和qdelt[14..0]才是当前符号的小数倍频率偏移和采样钟频率偏移估计值。波形中的估值与实际数据的对应关系如表4.1所示。

图4.2 小数倍频偏和采样钟偏移估计单元的电路仿真波形图

表4.1 波形图中数据与实际数据对照表
小数倍频率偏移和采样钟频率偏移模块是在整偏校完之后才有效,此时的小数倍频率偏移是经过时域粗偏估计校正后的剩余部分。表4.1列出波形中的估值与实际数据的对应关系。从表中的数字对应关系可以看出,电路中估计的小数倍频偏与实际频偏的差在0.1%以内。采样钟偏移估计值与实际偏移误差为1ppm左右,这已满足了采样钟的粗调精度;相位输出为前后符号的小数倍偏频所引起的相位旋转。由此单元电路,可以准确地估计出小数倍频偏和采样钟偏移及其相位。
细定时同步估计的电路仿真
图中的data_re_in[15..0]和data_im_in[15..0]表示经公共相位校正后的复数据实虚部;syn_in是输入有用数据的起始位置脉冲;sym_type[1..0]是前端输入的符号类型;taok[22..0]和td[9..0]分别为估计的符号定时偏移和其整数部分;syn_tao是taok[22..0]的有效数据起始脉冲信号。

图4.3 符号定时偏移估计单元的电路波形图
图4.3中共有9个符号。由于本算法利用了4个符号的散布导频,故图4.3中,从第四个符号的结束处开始,在syn_tao后的taok[22..0]才是当前符号的定时偏移估计值。波形中的估值与实际数据的对应关系如表4.2所示。

表4.2 波形图中数据与实际数据对照表
表4.2中的定时实际偏移为-112,而不是仿真条件中的-100,这是由于在瑞利信道的仿真模型中,符号定时同步头位置(重心位置)是在第一条径之后12个采样点出现的。由表中数据对应关系可知,符号定时偏移估计单元可准确地估出符号定时偏移的整数部分。由于采样钟偏移、算法估计误差及电路运算误差的影响,其小数部分不为零,这与电路的仿真结果一致。
改进前后占用硬件资源比较
表4.3给出了改进前后,频域同步所占用的硬件资源比较,其中ALUTS、Registers、Memorybits、DSPblock9-bitelements分别为自适应查找表、寄存器、存储器和9字节DSP处理块。通过比较可以发现,改进后的方案可以节省大量的硬件资源。

表4.3 改进前后的硬件资源对比
结束语
频率偏移估计可以分为整数倍频偏估计单元、小数倍频偏、采样钟偏移估计单元和符号定时偏移估计单元。本文主要介绍各部分的算法方案及电路实现时所用的FPGA元件的基本结构、设计思路。最后通过对电路的仿真波形可以看出,这些频域同步算法和FPGA电路能够满足多载波传输系统的同步要求。
- DSP芯片在水下目标检测与参数估计中的应用 (07-08)
- 基于DSP的水下目标检测与参数估计应用(01-27)
- 基于FPGA的PUSCH信道估计仿真与实现(06-05)
- 基于FPGA实现视频图像的一种运动估计设计(06-05)
- 数字基带预失真系统中环路延迟估计的FPGA实现(06-05)
- 基于复数浮点运算的协方差矩阵的FPGA实现(06-05)
