PIC单片机浮点数格式及其与十进制数之间的转换和程序设计步骤

在我们设计的仪表中采用PIC系列单片机，碰到了浮点数的运算问题，查阅其有关资料发现，其浮点数的格式及其与十进制数之间的转换，与我们常用的MCS-51单片机所提供的三字节、四字节浮点数完全不同，本文将说明其浮点数的格式及其与十进制数之间的转换和程序设计步骤。

1 浮点数的格式

Microchip公司单片机所采用的浮点数格式是IEEE-754标准的变异型。32位浮点数格式为:



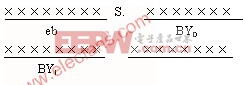
其中：×表示一位二进制数0或1；eb为指数的偏差;S为浮点数的符号位，S=0为正数，S=1为负数；小数点“?”在符号位S的右边；BY0BY1BY2为尾数的小数部分。

应特别注意：

⑴浮点数隐含其整数部分为1。

⑵十进制数0的浮点数表示为00H,00H,00H,00H。

2 浮点数与十进制数之间的相互转换

2.1 十进制数转换成浮点数

设:十进数为A,则2Z=A，Z=lnA/ln2，指数P=int(z)；尾数部分X:X=A/2P,其整数部分隐含为1(零除外),将其小数部分按原码格式化为二进制数,即为尾数的小数部分BY0BY1BY2。而指数偏差eb=P+7FH(其中的7FH为指数的偏移量)。符号位S,视十进制数的正负而确定。

例如十进制数50.265化为32位规格化浮点数：A=50.265，则Z=ln50.265/ln2，P=int(Z),故P=5;X=A/2P=50.265/25=1.57078125，将0.57078125化为23位二进制小数，即是BY0BY1BY2，在最高位添上十进制数的符号位S（因十进制数为正数，故S=0）；而eb=P+7FH,所以，十进制数50.265的32位规格化浮点数即为84H，49H，0FH，5CH。

2.2 浮点数转换为十进制数

设浮点数为ebS.BY0BY1BY2。由于浮点数隐含尾数的整数为1,故尾数X的实际值为:

BY0BY1BY2；指数P=eb－7FH;故:十进制数

A=(－1)S×2P×X

例：32位规格化浮点数84H,49H,0FH,5CH转换为十进制数。

符号位S=0；指数P=84H－7FH，故P=5;尾数的小数部分为49H,0FH,5CH左移一位，而尾数的整数部分隐含为1，故尾数X的实际值为：1.57078123；十进制数A=(－1)0×25×1.57078123，即A=50.265。

3 浮点数与十进制数相互转换的程序设计

3.1 浮点数转换为十进制数的程序设计

(1)检测浮点数是否为零；若为零，则十进制数整数部分和小数部分均为零。

(2)保存浮点数的符号位，将浮点数隐含的1置于浮点数的符号位，指数偏差eb加1，小数点移到原浮点数的符号位之前。

(3)判断指数偏差大于7FH否？若小于等于7FH,则该进制数整数部分为零，浮点数尾数部分右移n次(注：n=7FH－指数偏差eb),即求得二进制小数部分。若大于7FH,则将小数点右移n’次(注:n’=指数偏差eb－7FH)，即求得二进制整数部分和小数部分。

(4)将二进制整数部分转换为十进制整数；将二进制小数部分转换为十进制小数。至此，完成了浮点数到十进制数的转换。

3.2 十进制数转换为浮点数的程序设计

(1)检测十进制数是否为零，若为零，则浮点数置成00H,00H,00H,00H。

(2)保存十进制数的符号位，将十进制数的整数部分转换为二进制整数，将十进制数的小数部分转换为二进制小数(设二进制整数为三个字节，二进制小数为两个字节)。

(3)将浮点数的指数偏差eb置为7FH+23，检测二进制整数的最高位是否为1，不是，则将二进制整数和二进制小数联合左移，左移一次，指数偏差减1，直至二进制整数的最高位为1;隐含尾数整数的1，将二进制整数的最高位改为数的符号位。至此，指数偏差eb单元及原二进制整数的三个单元中的内容，即构成四字节浮点数。

最后应该指出，本文所述32位浮点数，精度相当于7位十进制数；32位浮点数运算程序在Microchip公司提供的有关资料中均有,但是,在调试其浮点子程序时,发现0减0的结果为00H,80H,00H,00H,而不是00H,00H,00H,00H，编程时应注意。

4 结语

本文中的十进制数与浮点数之间相互转换的程序设计，在智能化仪表的键盘置数及数据显示中，具有实用价值。这里提出了一种设计思路，没有复杂的算法，程序设计亦较简单，工作量较少，可利用Microchip公司提供的现成子程序实现十进制整数与二进制整数的相互转换，十进制小数与二进制小数的相互转换。