用振荡器采样随机数发生器保证网络SoC设计加密算法的安全性
从几种不同类型的振荡器中进行选择,包括差分振荡器、单端振荡器及混合振荡器,不同类型振荡器对不同噪声源的敏感度也不一样。显而易见,不同振荡器的特性比较需要丰富的知识,本文在此只作简单讨论。 通常,差分振荡器对电源及基底噪声的敏感度不如单端振荡器。这是因为差分放大器对的电源和接地点会同时出现电压摆动,所以两个输入之间的差值保持一致,输出也一致,呈现出较高的共模抑制比(CMRR)。差分逻辑常用于模拟逻辑压控振荡器设计中,例如锁相环中的振荡器,因为锁相环需要较高的CMRR,所以差分振荡器方案并不特别适用于那些需要非确定噪声源的设计。另一方面,单端反相振荡器极易受电压摆动或输入信号中直流分量的影响,如果噪声对电平带来任何波动,都会影响振荡器的抖动。此外,差分、感容及张弛振荡器设计需要客户定制的电路布局,所以无法集成到标准单元的SoC设计中。因此,在SoC设计中最简单直接的解决方案通常是单端环形振荡器(图4)。 尽管单端环形振荡器有这样的优势,在选用时还是有一些复杂因素必须考虑。由于高速数字系统存在切换动作,因此热噪声与电源/基底噪声相比一般可以忽略不计。电源和基底噪声是引起噪声耦合的主要原因,噪声耦合的振荡器在反相电路中会产生δ延迟。电源电压变化或来自基底耦合的噪声会改变每级电路输出节点的电容,从而使振荡器的总频率不断改变。此外,除热噪声外,所有环形振荡器延迟电路级中的电源和基底噪声都是相关的,所以如果没有牢靠的接地环保护电路,设计人员都不希望让两个振荡器电路靠得太近。如果屏蔽不是很好,会造成两个位流源之间的随机性相互关联。在最终的振荡器设计中,所有这些因素都必须要考虑到。 此外,就算设计人员有良好的意愿,实施方案也可能无法产生真正的随机位流。设计人员或许要借助一些成本高昂的额外测试来保证随机数发生器系统能产生期望的结果。如前所述,随机性主要来自电源和基底噪声与振荡器电路的耦合,由于这些振荡器会耦合同一个噪声源,因此设计人员不希望将它们靠得太近。进一步来说,如果两个振荡器锁定在同一个噪声源上并相互耦合,那么它们之间的相关性也会增加,从而使两个源的随机输出相互关联。如果在最终布局上将两个振荡器分开,电源和基底噪声的相关效应便可减轻。 采用振荡器采样法的一种常见做法是多设计一对振荡器,万一主随机源失效了,它还可以降低RNG系统没有非确定性噪声源的风险,随后通过一个强大的混合函数将采样位流进行混合,以便保留各个源固有的随机性,这一点将在后面详述。为了从混合位流中获得更好的随机性,必须给各振荡器选择一个独特的主标称频率,或者使其频率能够调节,这可尽量减少多个源之间的互相关性。当然,设计者必须权衡考虑,要么接受额外成本,要么承担不能生成真正随机数的风险。 偏差纠正器 振荡器采样法的工作基于这样一个事实,即高频振荡器一直保持50%的占空比,而低频振荡器每个周期都有明显变化。如果情况不是这样(尽管绝大部分情况下是这样),所获得的位码便会出现偏差,既可能是“1”,也可能是“0”,这称为偏移。幸运的是我们可以采取有效的后处理方法来纠正偏差,以一种确定的方式产生分布更均匀的位流。其中两种最简单的技术分别称为奇偶生成和转换映射,此外还有一些较复杂的偏差纠正方法,包括使用快速傅利叶变换函数和更复杂的位混排技术,它们通常采用延迟元件和反馈通路组合来去除位与位之间的相关性。 偏差纠正的目标是对位流进行均衡分配,以便以相同的概率产生“1”和“0”,其做法基本上是从有偏差的位序列中提取出更随机的数值。这种后处理功能并非振荡器采样技术所独有,其应用对原始噪声源没有要求,要实现这种功能也并不复杂。一种简单方法是奇偶生成,它具有鲁棒性强的优点,可用于更大范围的偏差分布。用硬件来实现固定长度位采样序列一般非常简单,例如简单的级联XOR链便可有效用作一个奇偶生成器并完成适当的偏差纠正(图5)。 转换映射也叫做冯·诺依曼纠正器,它将一对采样输入位转换成一个输出位,例如把输入对[0,1]转换成1,把[1,0]转换成0,而在输入为[0,0]或[1,1]时什么也不输出。这种技术可以完全消除偏差,但其代价是必须在输入位之间创建一个不定量的延迟,并产生一个输出位长的任意数。 混合函数 即使采用了所有上述技术,仍然存在这样一些担忧,即由于存在多种非随机数据源(如前面提及的多个振荡器源组合),系统固有的随机性可能受到影响。采用功能强大的混合函数可以确保随机源的随机性,这些函数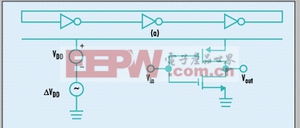
- IP核在SoC设计中的接口技术 (08-06)
- 视频跟踪算法在Davinci SOC上的实现与优化(10-06)
- 基于赛灵思Spartan-3A DSP的安全视频分析(02-17)
- Linux下Sniffer程序的实现(06-12)
- linux操作系统下的进程通信设计(01-24)
- 基于S3C44B0X和uClinux的Socket通信实现(02-28)
