数字下变频(DDC)中坐标变换模块的ASIC实现

1．引言

数字下变频(DDC)技术是软件无线电接收机的核心技术。其基本功能是从输人的宽带高速数字信号中提取所需的窄带信号，将其下变频为数字基带信号，并转换成较低的数据率，以供后续的DSP作进一步的处理。目前许多型号的DDC芯片事实上其功能己远远不只是下变频，还包括了成形滤波器、定时同步内插滤波器、重采样NCO、坐标变换、数字ACC等功能，其结构如图1所示。

CORDIC(Coordinate Rotation Digital Computer)是一种迭代算法，它提供了计算三角函数和欠量求模的方法。该算法仅利用加法和移位两种运算通过迭代方式进行矢量旋转，因此，它非常适合于硬件A-SIC实现。本文所要阐述的就是基于CORDIC算法的数字下变频器中坐标变换模块的ASIC实现结构，该模块的主要功能是实现直角坐标系到极坐标系的变换，从而求得由I路信号和Q路信号构成的向量的幅度值和相位值，将得到的幅度信息返回给前级的数字AGC进行增益控制，还可以实现对FM信号的解调。

2．CORDIC算法与实现

2.1 CORDIC算法原理

CORDIC是一种迭代算法，它可以用来计算sin，cos等三角函数，计算幅值和相位等到所需的精度，CORDIC算法计算幅值和相位的原理如下：

假设直角坐标系内有向量A(Xn，Yn)，向量A顺时针旋转θn后得到向量B(Xn，Yn)，如图2所示。

向量A和向量B之间存在以下关系，用矩阵表示为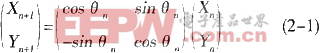

将cosθn提出以后得到

在这里我们取0i=arctan(1/2i)，所有迭代的总和为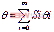，其中Si={-1，+1}，则tanθi=Si2-i，可得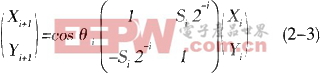

上式Si中的符号决定了向量的旋转方向，当时Yi≥0，Si=1，顺时针旋转；当Yi0时，Si=-1，逆时针旋转，式中的cosθi=cos(arctan(1/2i)，随着迭代次数的增加它收敛于一个常数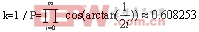，我们暂不考虑这个常数增益，这样式(2-3)就变为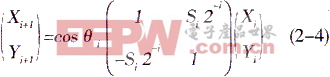

设总共旋转的角度为，初值为0，则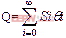，给定向量 一组初值如下

从上面的式子可以看出，当向量A旋转到X轴时，可以得到迭代的结果为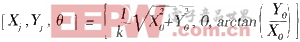 ，即可求得向量A的幅值和相位。由式(2-4)可知每次旋转的角度的正切值都是2的负幂次，在硬件实现时只需要执行右移和相加运算就可以实现每次迭代，易于硬件的实现。

2.2 用CORDIC算法的流水结构实现坐标变换

CORDIC迭代结构如图3所示，采用流水结构每次迭代完成一次旋转，每级迭代都用寄存器寄存，这样每个时钟周期都可以计算出一次幅度和相位。迭代的次数越多，精度越高，当然耗费的资源也就越多。

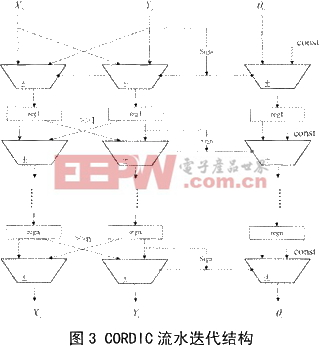
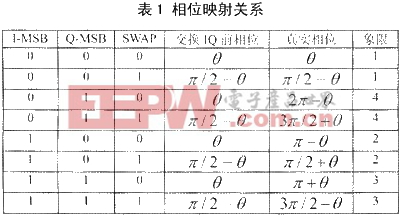
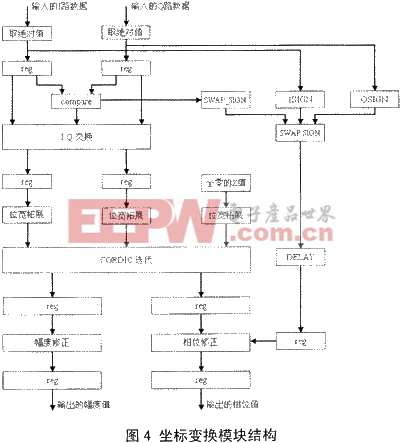
在数字下变频器输出I，Q两路信号后(输出信号用补码表示)，用CORDIC实现坐标变换时，为简化电路结构，只用计算的相角，其他象限的相角，采用处理后再映射的办法求取，冈此，对刚进入的数据会进行预处理。首先就是求输人数据的绝对值，并记录符号位作为处理后象限映射的依据。接下来，会判断I，Q两路数据的大小关系，并将较小的值交换到Q路，这样做的目的是要在同样的迭代次数下，达到更高的迭代精度。进入CORDIC迭代单元前会对I，Q两路数据进行位宽拓展，从而保证CORDIC迭代过程中，不会因截断误差造成太大的偏差。经过CORDIC迭代后所得的幅度值是有增益的，此时需要对其进行修正，另一方面，相位值需根据先前记录的I，Q两路数据的符号位和I，Q两路数据交换的情况作象限映射，表1列出了相位映射的规则。坐标变换模块的实现结构如图4所示。

2.3 使用modeIsim仿真的结果

图5是当输入激励为I路：sin(sin2πf)；Q路：COS(COS2πf)时的modelsim仿真结果，由图中可以看出坐标变换得出的相位值是一个标准正弦信号，幅度值为恒定值，幅度相位完全正确。

2.4 硬件实现结果

在硬件实现时，用verilog语言对坐标变换模块进行描述，为满足DDC的精度要求进行了18次迭代，并用DC基于UMC0.18μm的库进行了综合，硬件实现结果如图6所示。

图6(a)是DC综合后的面积报告，图6(c)是关键路径的时序报告，综合后的最大路径延时为9.77ns，完全可以满足本模块数字下变频器100MHz的处理速度要求，综合出的单元(cell)的总面积仅为0.27。图6(b)是该设计在FPGA上验证的结果，该DDC的工作频率为80MHz，通道2为输入的基带信号频率20kHz，载波频率5MHz，频偏200KHz的FM信号，通道1是通过DDC下变频后交给坐标变化模块的I，O两路信号求出的相位信息，即频率为20kHz的正弦信号，由图可知该没计实现了坐标变换功能。

3 结论

使用CORDIC算法，并用流水结构实现幅度相位的求取可以获得较高的处理速度，增加迭代次数可以获得更高的处理精度，但会耗费较多的资源，在设计时应根据需要，合理的确定迭代次数。该设计已成功应用于高速数字下变频芯片中。