编写延时函数的简单方法
这里用一个例程详细介绍一下。
过程参考如下:
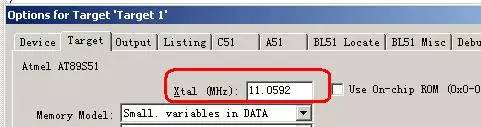
在编译器下建立一个新项目,也可以利用已有项目。此过程中需要注意,单片机晶振的选择,因为for循环里指令的执行时间和晶振有直接关系,本例中晶振使用11.0592M。
编写一段关于延时的函数,主要利用for循环,代码如下:
void delay_ms(unsigned int ms)
{
unsigned int i;
unsigned char j;
for(i=0;i
{
for(j=0;j<200;j++);
for(j=0;j<102;j++);
}
}
其中ms是输入参数,如果输入1,就是要求程序延时1ms。
j变量是调整程序运行的时间参数。调整j的数值,使1次循环的时间在1ms。
将此程序编译通过,然后利用软件仿真,调整时间。
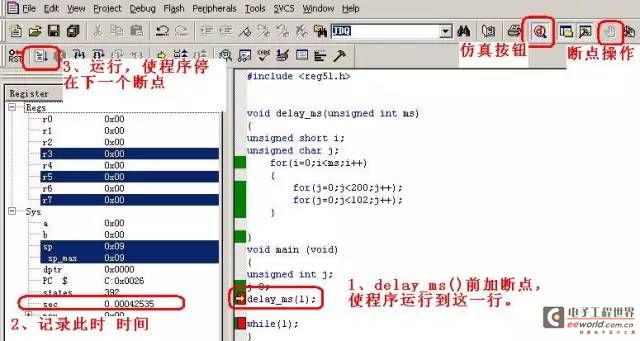
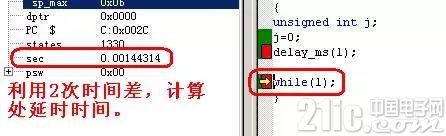
下面这个sec就是程序运行到现在的这一行所用的时间。
两次时间差就是延时函数使用的时间,如果与1ms相差比较多,用户可以调整j参数的值,使延时时间尽量接近1ms。如增大j的值for(j=0;j<105;j++);
此方法得出延时函数,在晶振不同的情况下,延时时间会不准。软件调试结果,这个程序的延时时间为:1.01779ms,一般的单片机系统中都可以应用。
下面来说说汇编的传统计算方法:
指令周期、机器周期与时钟周期
指令周期:CPU执行一条指令所需要的时间称为指令周期,它是以机器周期为单位的,指令不同,所需的机器周期也不同。
时钟周期:也称为振荡周期,一个时钟周期 =晶振的倒数。
MCS-51单片机的一个机器周期=6个状态周期=12个时钟周期。
MCS-单片机的指令有单字节、双字节和三字节的,它们的指令周期不尽相同,一个单周期指令包含一个机器周期,即12个时钟周期,所以一条单周期指令被执行所占时间为12*(1/12000000)=1us。
了解了上面这些我们来看一个例子
;============延时1秒子程序========================
DELAY_1S: ;延时子程序,12M晶振延时1.002035秒
MOV R4,#10
L3: MOV R2 ,#200 ;1指令周期
L1: MOV R3 ,#249 ;1指令周期
L2: DJNZ R3 ,L2 ;2指令周期
DJNZ R2 ,L1 ;2指令周期
DJNZ R4 ,L3 ;2指令周期
RET ;2指令周期
;循环体延时时间: [(249*2+1+2)*200+1+2]*10*12/12000000=1.002030s
;加上ACALL指令和第一条mov指令以及最后一条RET指令算出来整个函数的时间为1.002035s
;================================================
通常选用的是11.0592MHZ的晶振:
[(249*2+1+2)*200+1+2]*10*12/11059200=1.08727213541666666...S
汇编延时子程序的延时计算问题
对于程序
DELAY: MOV R0,#00H
DELAY1: MOV R1,#0B3H
DJNZ R1,$
DJNZ R0,DELAY1
查指令表可知 MOV一个机器周期,DJNZ 指令需用两个机器周期,而一个机器周期时间长度为12/11.0592MHz,所以该段程序执行时间为:
((0B3×2+1+2)×256+1)×12÷11059200=100.2789mS
第一层:DJNZ R1,$:执行了B3H次,一次两个周期,所以为0B3×2;
第二层:MOV R1,#0B3H为一个周期,DJNZ R0,DELAY1为两个周期,这样循环一次就是0B3×2+1+2个周期;第二层的执行次数本来是255次,但因为赋首值为0,而DJNZ是先减1,再比较的,所以就应该是256次。
这样的话,整个循环执行完应该是(0B3×2+1+2)×256+1次。再加上开始赋值这一句,就是((0B3×2+1+2)×256+1)了
还说明一下:
nop指令或者_nop_(); 函数占一个机器周期,在stc单片机的12T模式下一个机器周期是一个振荡周期的12分频,如果你的晶振是12MHZ,那你的一个机器周期就是1微秒.一个nop指令的执行时间也就是1US
当在6T模式(下载的时候可选择模式)下12M晶振的时候,一个nop就是0.5US了.
延时函数简单方 相关文章:
- Windows CE 进程、线程和内存管理(11-09)
- RedHatLinux新手入门教程(5)(11-12)
- uClinux介绍(11-09)
- openwebmailV1.60安装教学(11-12)
- Linux嵌入式系统开发平台选型探讨(11-09)
- Windows CE 进程、线程和内存管理(二)(11-09)
