从三方面分析噪声的来源

个样本之间的时间。在均匀分布中，所有样值都具有相同的概率。这种分布是有边界的。

最底下那张图显示的是同样具有边界约束的正弦分布。这种分布呈马鞍形状，最大概率发生在幅度极值点(最大和最小值点)。

在许多应用中，两个或多个随机过程可能发生交互。当这种情况发生时，过程的概率密度会进行数学卷积运算。一个常见的例子是结合了随机和确定性抖动分量的时序抖动。图5显示了结合在一起的高斯和正弦分量，源分布位于上面两张图，从上往下数的第三张分布图是两个源卷积的结果。许多先进的示波器提供可选的抖动或噪声分析包，这些分析包可以将这些组合式分布分开，单独测量分量。

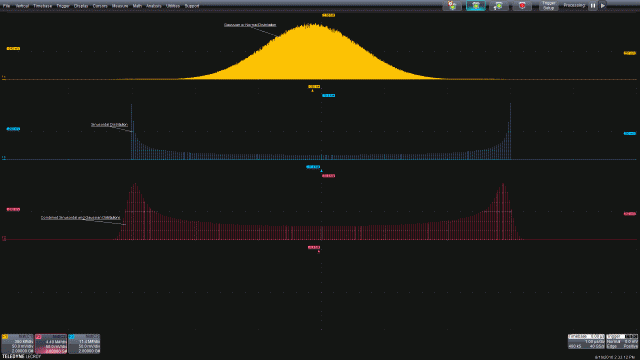
图5：当高斯和正弦分布组合在一起时形成的概率密度函数是两个源概率密度函数的卷积。

频域分析

单位频率上的功率(即功率谱密度PSD)是最常见的频域噪声分析工具。图6给出了一个例子，上部是带宽受限高斯噪声的时域图，下部是带宽受限噪声的功率谱密度。

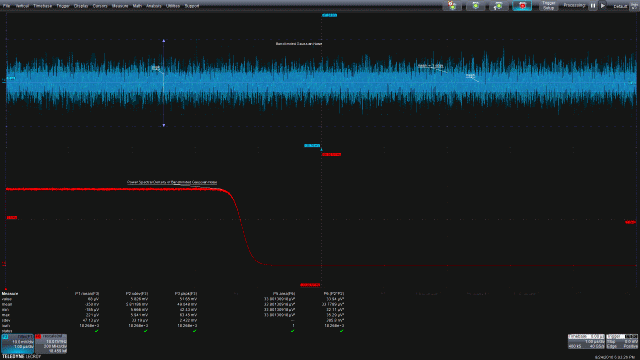图6：带宽受限的高斯噪声(上部)及其功率谱密度(下部)。功率谱密度曲线显示了每单位频率的功率与频率的关系。功率谱密度的单位是V2/Hz，曲线下方的面积就是信号的均方值或方差。

本例中功率谱密度的测量单位是V2/Hz。这条曲线是用示波器的快速傅里叶变换(FFT)计算出来的，选用的是输出类型幅度平方而不是默认的分贝(dBm)刻度。除了输出类型，我们还选择了矩形加权和最小素因数FFT。这种FFT可以报告分辨率带宽Δf，在本例中是100kHz，以及加权函数的有效噪声带宽(ENBW)，针对矩形加权的值为1.000。

为了计算功率谱密度，平均后的FFT输出必须被归一化为有效FFT带宽。此外，这个示波器的FFT输出经校准可读取峰值而不是均方根值。为了转换回均方根值，FFT幅度值必须乘上0.707，幅度平方值必须乘上0.5。必须使用Rescale数学函数将FFT值除以FFT的有效带宽才能将该值归一化为单位带宽(1Hz)。Rescale函数可以通过一个乘数因子并加减偏移量重新调整数值。在我们这个例子中，乘数是0.5/100E3 = 5E-6。乘数因子0.5在前面已经讨论过。另外一个因子是有效FFT带宽的倒数，是分辨率带宽乘以等效噪声带宽(ENBW)。如果选择了矩形以外的加权函数，ENBW将是大于1的值。Rescale函数还能改变单位，在本例中单位被设为V2/Hz。你可能已经注意到，再构造数学函数也已经用于将浮点FFT输出的映射优化进参数测量中使用的整数数学空间。

参数P2测量时域波形的标准偏差参数。P6使用参数数学公式实现标准偏差的平方，得到噪声信号的方差。参数P5代表功率谱密度曲线下方的面积，这个面积也是噪声信号的方差，只不过是从功率谱密度计算出来的。两种方法计算出来的方差值基本上是相等的，相差不到0.1%。

在频域中分析随机过程可以帮助你细分不同频率产生的噪声。本例中的面积测量可以覆盖整个FFT范围。你也可以使用测量选通门将测量限制在指定频带内，以判断特定频谱区域的噪声情况。在带宽等于FFT有效噪声带宽的情况下，示波器的光标可以读取特定频率处的功率谱密度。

派生参数

峰值因数，即波形峰值与均方根值之比，可以帮助你确定处理信号峰值变化所需的动态范围。虽然我们使用的示波器没有双极性"峰值"参数，但我们借助通道1中信号的绝对值可以很容易地创建一个。这样可以将负值"翻转"进波形的正值区域，进而让你使用最大值参数读取每次采集数据的最大正峰或负峰值。注意，这种方法是因为信号有零均值才起作用的。然后我们就可以使用参数数学公式计算峰值与均方根值之比的峰值因数。图7显示了这种测量。

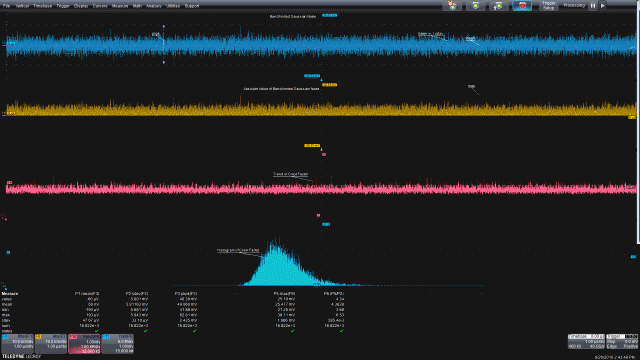
图7：测量峰值与均方根值之比的信号峰值因数。所测信号的绝对值使得所有峰值呈单极性，因此最大值参数返回的就是每次采集数据的最大峰值。参数数学公式可计算出最大值与标准偏差(均方根)值之比值，即峰值因数。

最上边的波形是带宽受限的噪声信号。参数P2是噪声波形的标准偏差(交流耦合的均方根值)。下面一个波形显示了噪声波形的绝对值，这个波形是单极性的。源波形中的最高正负峰值已成为最高绝对峰值。使用最大值参数得到这个参数。

参数P5是绝对波形曲线的最大值。参数P6使用参数数学公式计算每次采集数据的峰值因数，即P5(max)与P2(rms)的比值。P6参数统计显示了当前值、均值、最小最大标准偏差以及峰值因数测量值总数。在本例所示超过15000次采集中，峰值因数从3.68变到6.53，平均值为4.38。

从上往下第三张图是峰值因数的趋势曲线，按测量顺序显示了每一次测量的峰值因数。趋势图下方是峰值因数的柱状图。从图中可