PID公式的推导过程及实现代码

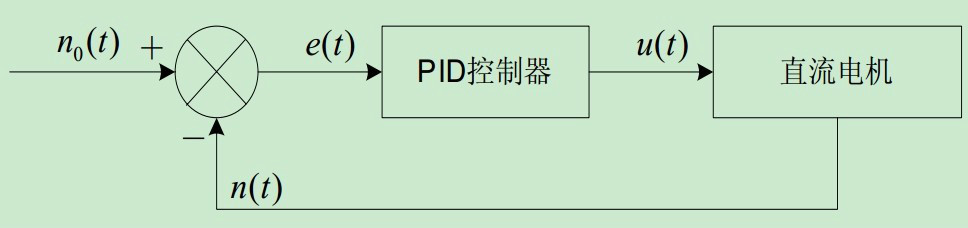
n0(t)是要稳定的值
n(t)是当前输出值
e(t) = n0(t) - n(t)

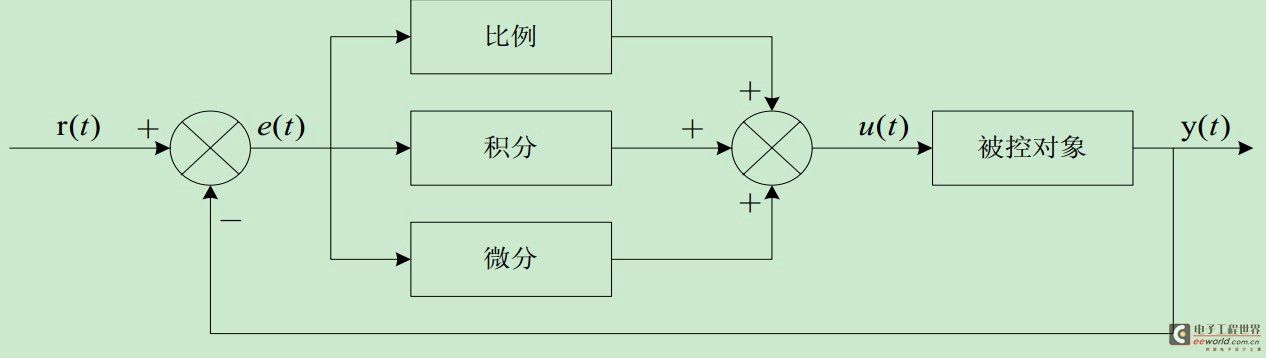
一、模拟PID控制原理

这个公式网络上很好找：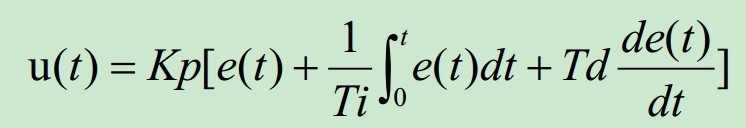

二、数字PID控制
由于模拟的微积分运算对应计算机来说是不太好写代码的，所以要利用采样将数据离散化

于是公式就可以转换为：

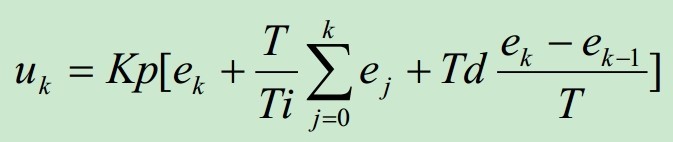
其中T为采样时间，由于T之类的参数是常量，所以将Kp乘入公式中可以转换成另一种写法
这个公式叫位置式算法

由于要不断的累加ej，增加了计算量，所以这个公式又可以转换为增量式算法：

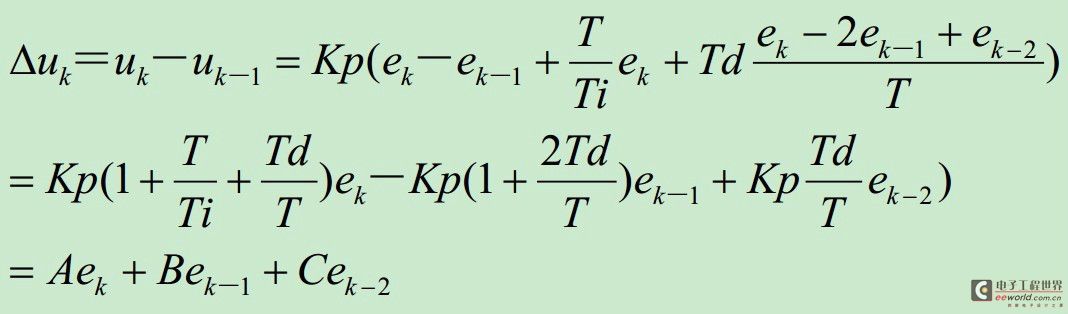
然后u(k) = u(k-1) + u

三、参数的整定
先将Ti设置为无穷大，Td设置为0，调节Kp
然后再调节Ti，最后是Td

四、实现代码

typedef struct PID
{
int SetPoint; //设定目标 Desired Value
longSumError; //误差累计

double Proportion; //比例常数 Proportional Cons
double Integral; //积分常数 Integral Const
double Derivative; //微分常数 Derivative Const

int LastError; //Error[-1]
int PrevError; //Error[-2]
} PID;

/*******************************************************************************
* 函数名称 : IncPIDCalc
* 函数描述 : 增量式 PID 控制计算
* 函数输入 : int 当前位置
* 函数输出 : 无
*函数返回 : 增量式PID结果
*******************************************************************************/
int IncPIDCalc(int NextPoint)
{
int iError, iIncpid;
//当前误差
iError = sptr->SetPoint - NextPoint;
//增量计算
iIncpid = sptr->Proportion * iError //E[k]项
- sptr->Integral * sptr->LastError //E[k－1]项
+ sptr->Derivative * sptr->PrevError; //E[k－2]项
//存储误差，用于下次计算
sptr->PrevError = sptr->LastError;
sptr->LastError = iError;
//返回增量值
return(iIncpid);
}

/*******************************************************************************
* 函数名称 : LocPIDCalc
* 函数描述 : 位置式 PID 控制计算
* 函数输入 : int 当前位置
* 函数输出 : 无
*函数返回 : 位置式PID结果
*******************************************************************************/
int LocPIDCalc(int NextPoint)
{
int iError,dError;

iError = sptr->SetPoint - NextPoint; //偏差
sptr->SumError += iError; //积分
dError = iError - sptr->LastError; //微分
sptr->LastError = iError;

return(sptr->Proportion * iError //比例项
+ sptr->Integral * sptr->SumError //积分项
+ sptr->Derivative * dError); //微分项
}